Угол между двумя плоскостями. Условия перпендикулярности и параллельности двух плоскостей

1. Составить уравнение плоскости, проходящей через точку 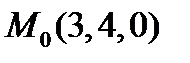и перпендикулярной двум плоскостям 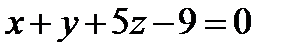и .

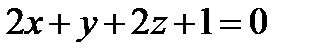2. Составить уравнение плоскости, которая проходит через точк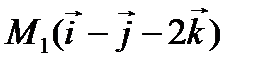и и 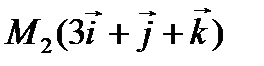перпендикулярно плоскости .

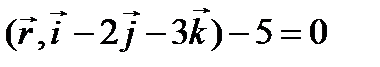Тема № 7.Теория определителей

1. Найти число нарушений порядка и определить четность перестановок: (124563), (987654321), (432159876).

2. С какими знаками входят в формулу для вычисления определителя матрицы пятого порядка слагаемые , ?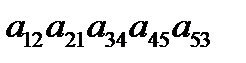

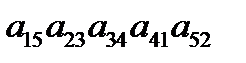3. Выяснить, какие из приведенных ниже произведений входят в определители соответствующих порядков и с какими знаками 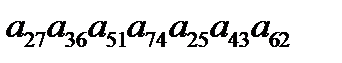(не вх.), (+).

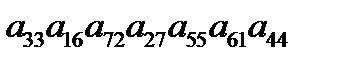4. Пусть матрица А порядка nсодержит n элементов равных 1, а остальные – нули. Чему может быть равен определитель матрицы А? (Ответ обосновать)

5. Доказать, что определитель диагональной матрицы равен произведению ее диагональных элементов.

6. Доказать, что определитель треугольной матрицы равен произведению ее диагональных элементов.

7. Используя свойства определителя доказать следующие тождества (определитель не развёртывать): .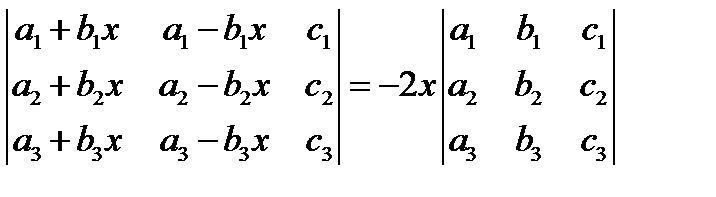

8. Используя свойства определителя доказать следующие тождества (определитель не развёртывать): .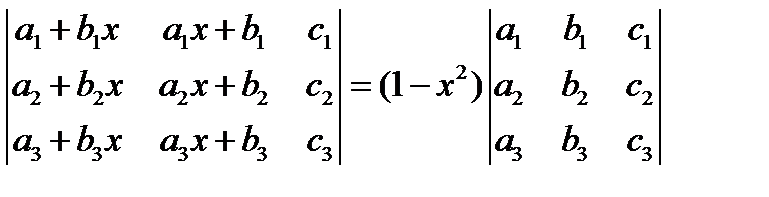

9. Вычислить определитель, разлагая его по элементам 2-го столбца: . ( )

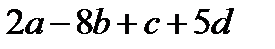10. Используя теорему разложения вычислить определители: а) 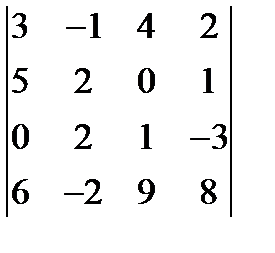, (223) б) 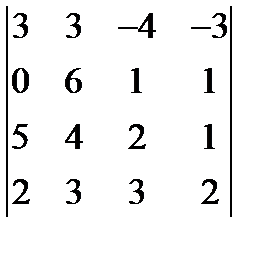. (-1)

11. Используя теорему разложения вычислить определители: а) 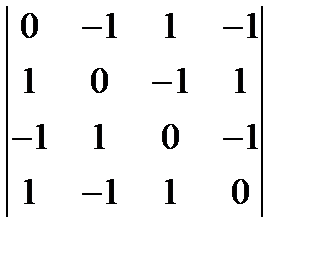, (1) б) 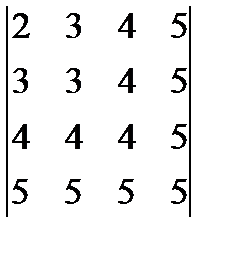. (-5)

12. Используя теорему разложения вычислить определитель .

13. Используя теорему разложения вычислить определители: а) 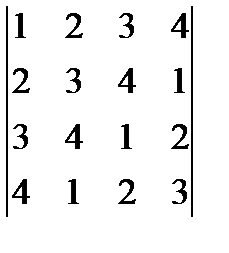, (160) б) . (2)

14. Используя теорему разложения вычислить определители: а) 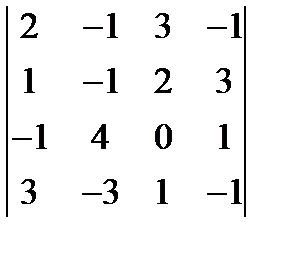, (-75) б) 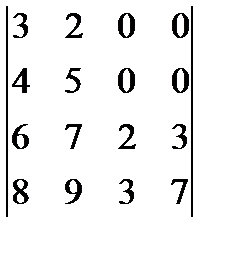. (35)

15. Используя теорему разложения вычислить определитель . (-4)

Тема № 8. Теория систем линейных уравнений

1. Решить систему уравнений методом Крамера 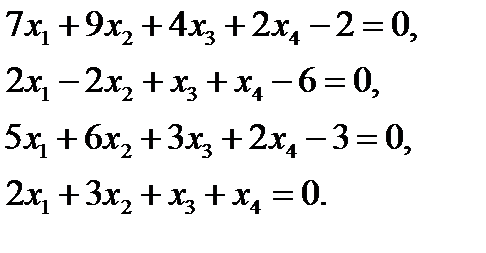ответ: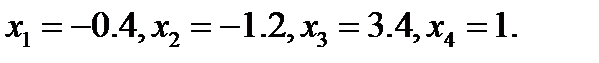

2. Решить систему уравнений методом Крамера 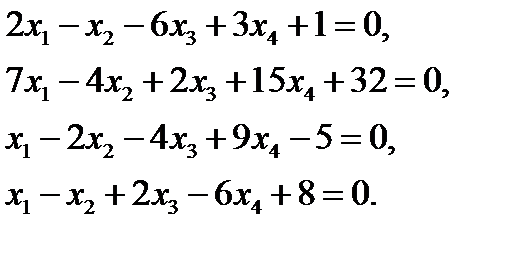ответ: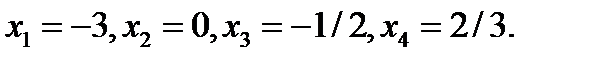

3. Решить систему уравнений методом Крамера 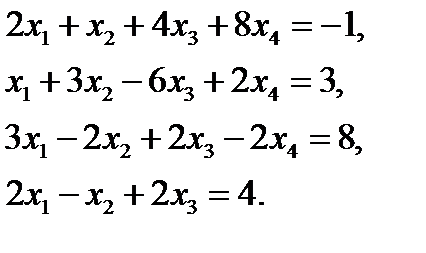ответ: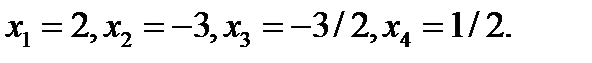

4. Решить систему уравнений методом Крамера 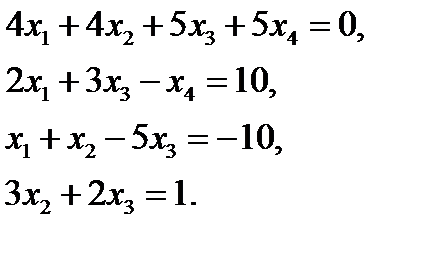ответ: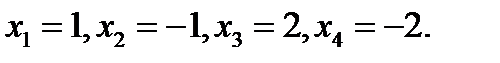

5. Решить систему уравнений методом Крамера 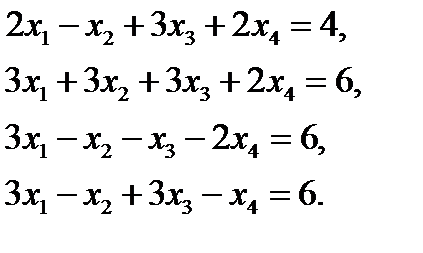ответ: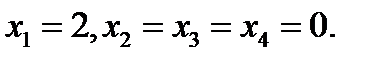

6. Решить систему уравнений методом Гаусса 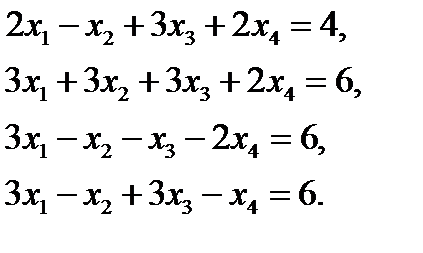ответ: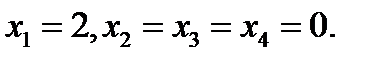

7. Решить систему уравнений методом Гаусса 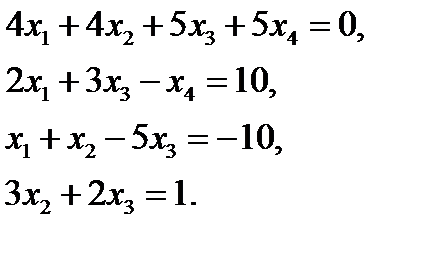ответ: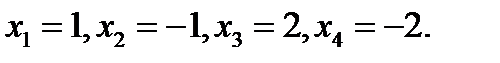

8. Решить систему уравнений методом Гаусса 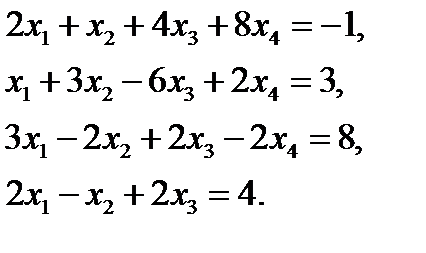ответ: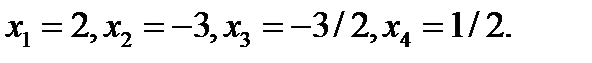

9. Решить систему уравнений методом Гаусса 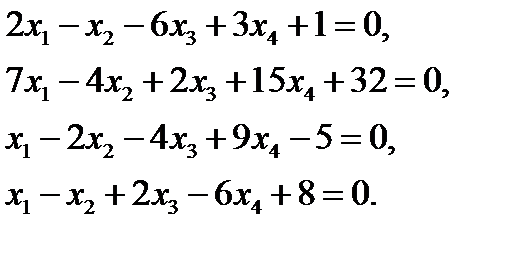ответ: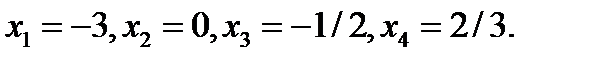

10. Решить систему уравнений методом Гаусса 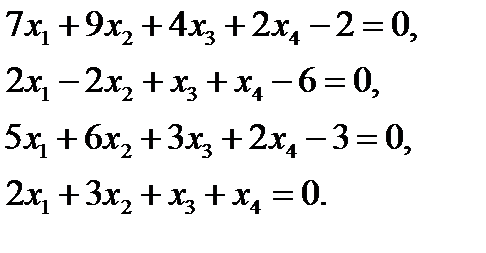ответ: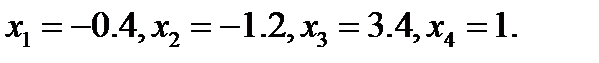

11. Решить систему уравнений методом Гаусса 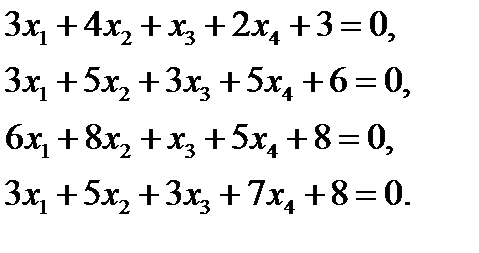ответ: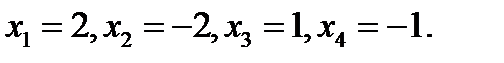

12. Решить систему уравнений методом Гаусса 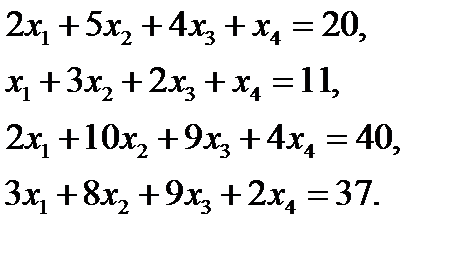ответ: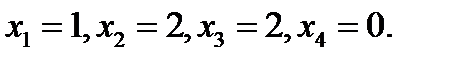

Тема № 9. Теория матриц. Действия над матрицами

1. Найти ранг матрицы: 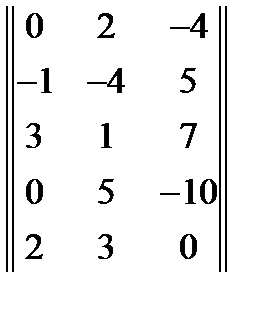. Ответ =2

2. Найти ранг матрицы: 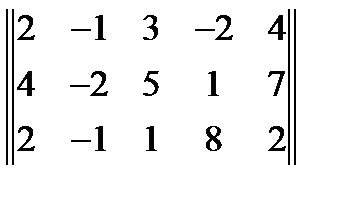. Ответ =2

3. Найти ранг матрицы: 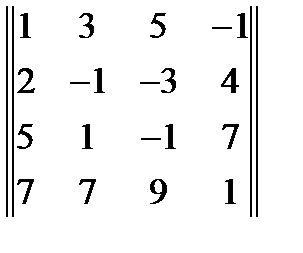. Ответ =3

4. Найти ранг матрицы: 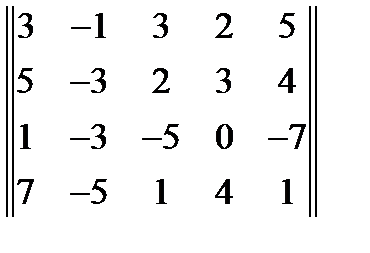. Ответ =3

5. Найти ранг матрицы: 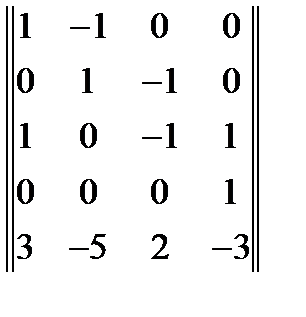. Ответ =3

6. Найти ранг матрицы: 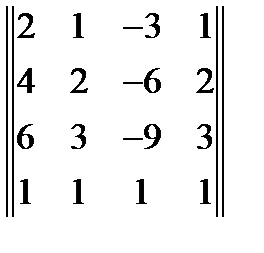. Ответ = 2

7. Найти ранг матрицы: 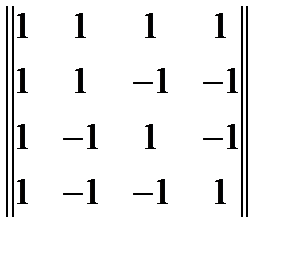. Ответ =4

8. Найти ранг матрицы: 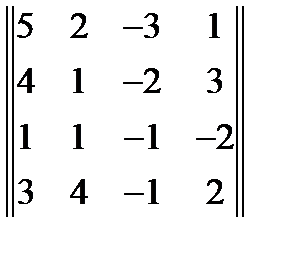. Ответ =3

9. Найти ранг матрицы: . Ответ =3

10. Найти ранг матрицы: 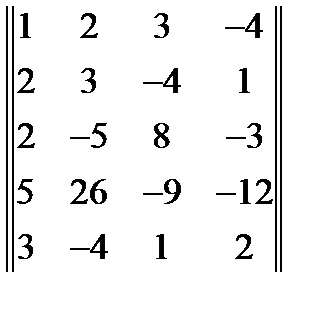. Ответ =3

11. Найти ранг матрицы: 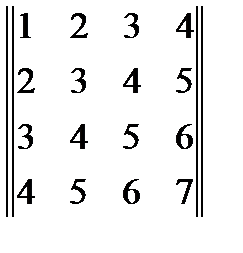. Ответ =2

12. Решить систему линейных уравнений с помощью обратной матрицы: 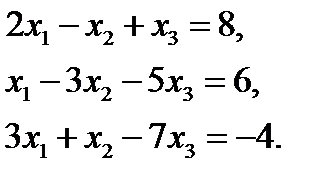Ответ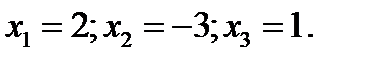

13. Решить систему линейных уравнений с помощью обратной матрицы: 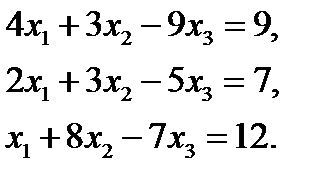Ответ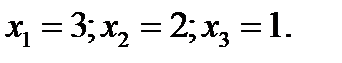

14. Решить систему линейных уравнений с помощью обратной матрицы: 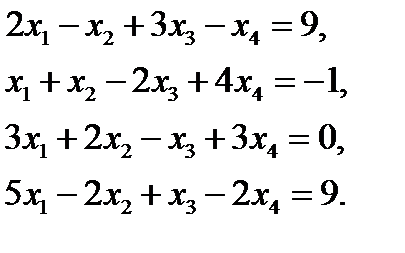Ответ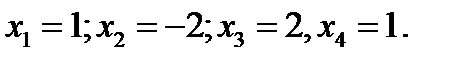

15. Вычислить: .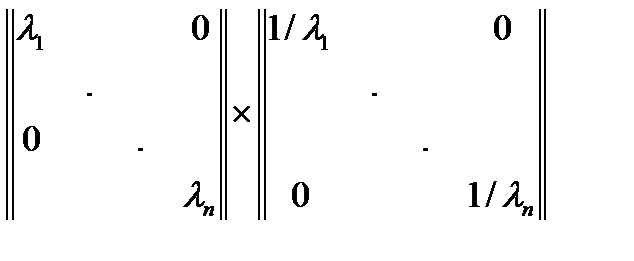

16. Даны матрицы: 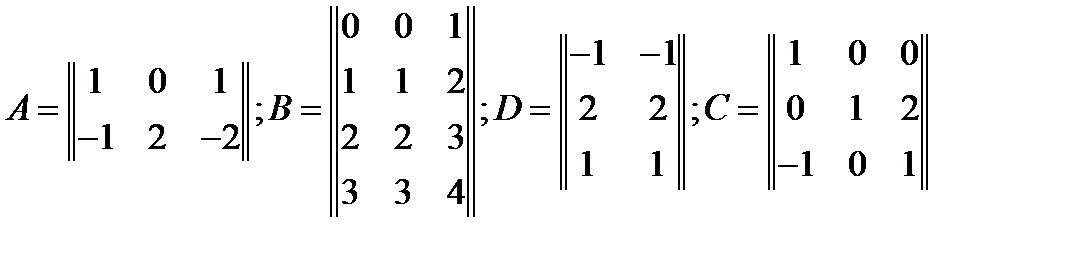. Найти произведения АС, ВСDA.

17. Даны матрицы: 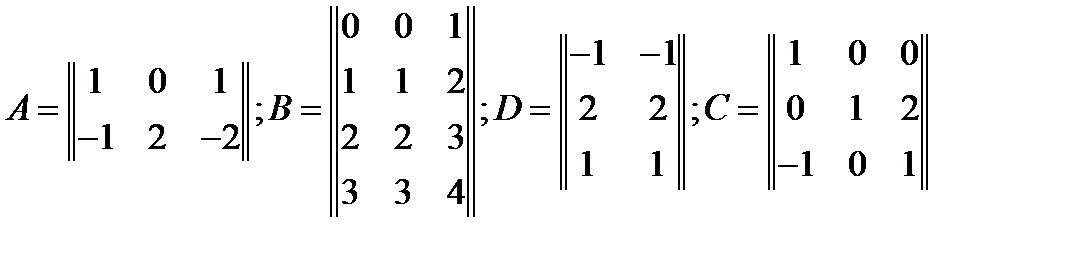. Найти произведения ВС, АСD.

18. Даны матрицы: 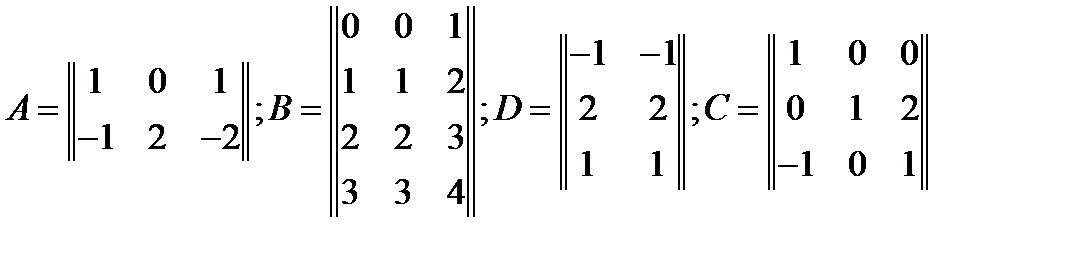. Найти произведения BC, ВСDA.

19. Вычислить: .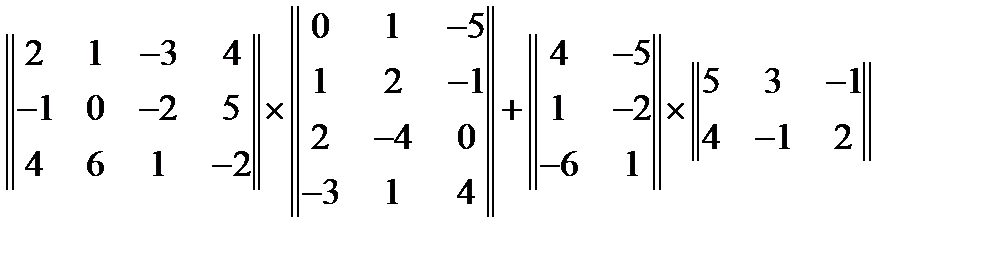

20. Методом присоединенной матрицы найти матрицу обратную к матрице 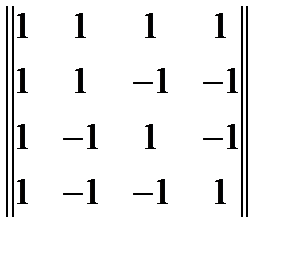. Ответ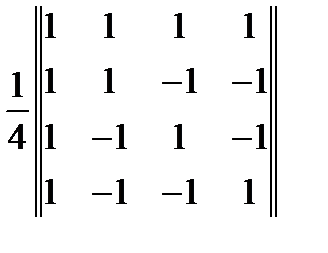

21. Методом присоединенной матрицы найти матрицу обратную к матрице 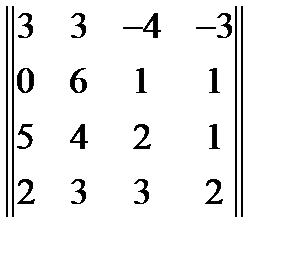. Ответ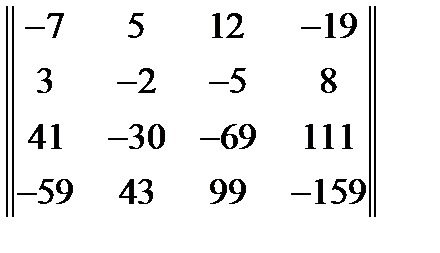

22. Методом присоединенной матрицы найти матрицу обратную к матрице 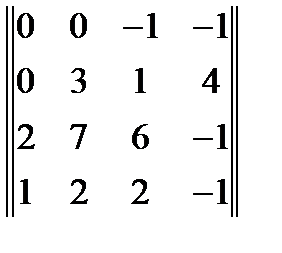. Ответ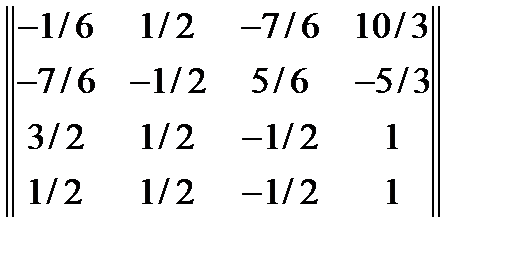

Список литературы

1. Сборник задач по математике для втузов (в трех частях). Под редакцией А.В. Ефимова и Б.П. Демидовича. – М. Наука. 1981г.

2. Апатенок Р.Ф. и др. Сборник задач по линейной алгебре и аналитической геометрии. – Минск. Вышэйш. Шк. 1990г. 285с.

3. Бахвалов С.В. и др. Сборник задач по аналитической геометрии. М. Наука 1964г.

4. Задачник практикум по аналитической геометрии и высшей алгебре. ЛГУ им. Жданова под общ. редакцией В.А. Волкова. – Ленинград. Изд. ЛГУ, 1986г. 259с.

5. Клетенник Д.В. Сборник задач по аналитической геометрии. М. Наука 1986г. 240с.

6. А.А. Бурдун, Е.А. Мурашко, М.М. Толкачев, … Сборник задач по алгебре и аналитической геометрии. Минск. 1989г. 258с.