Очно-заочной и заочной форм обучения
Очно-заочной и заочной форм обучения
Составитель: А.В. Терновой
Ковров 2013
УДК 539.3/6
С
Сопротивление материалов: Контрольные задания и методические указания для студентов заочного отделения [Текст]: / Сост.: А.В. Терновой А.В. – Ковров: ФГБОУ ВПО «КГТА им. В.А.Дегтярева»,2013.– 35 с.
Контрольные задания и методические указания для студентов очно-заочного и заочного отделения направлен на получение студентами практических навыков в самостоятельном решении задач по дисциплинам «Сопротивление материалов», а также по таким дисциплинам, как «Механика», «Прикладная механика», в которых рассматривается разделы курса "Сопротивление материалов".
Перечень представленных задач охватывает наиболее важные разделы дисциплины «Сопротивление материалов» и является универсальным при формировании структуры и содержания самостоятельной работы студентов всех специальностей, направлений (профилей) очно-заочной и заочной форм обучения, для которых эта дисциплина или ее разделы предусмотрены федеральными государственными образовательными стандартами и принятыми рабочими программами.
Табл.13 . Ил.12 , Библиогр.: 16 назв.
Рецензенты:
ISBN ////////////////////////
ОГЛАВЛЕНИЕ
Стр.
Введение …………………………………………………………………… 4
Общие указания…………………………………………………………… 4
Задачи контрольных заданий…………………………………………… 7
Тема 1. Геометрические характеристики
поперечных сечений бруса………………………………… 7
Задача № 1………………………………………………….. 7
Тема 2. Расчет конструкций на прочность и жесткость
при растяжении (сжатии)………………………………….. 8
Задача № 2………………………………………………….. 8
Тема 3. Расчет бруса на прочность и жесткость
при кручении…………….………………………………….. 10
Задача № 3………………………………………………….. 10
Тема 4. Расчет конструкций на прочность и жесткость
при изгибе………………..………………………………….. 11
Задача № 4………………………………………………….. 11
Задача № 5………………………………………………….. 13
Тема 5. Расчет статически неопределимой рамы………………. 14
Задача № 6…………………………………………………… 14
Тема 6. Расчеты при комбинированных видах нагружения
(сложное сопротивление)…..……………………………….. 16
Задача № 7. Косой изгиб..………………………………… 16
Задача № 8. Внецентренное растяжение-сжатие ...……………… 18
Задача № 9. Изгиб с кручением валов
круглого поперечного сечения…………….... 20
Тема 7. Расчет на устойчивость прямолинейного
сжатого стержня…..…………………………………………… 23
Задача № 10…………………………………………………… 23
Тема 8. Расчет конструкций при динамическом нагружении…..…. 25
Задача № 11. Расчет балки при ударном нагружении….. 25
Задача № 12. Свободные и вынужденные
колебания балок……………………..……… 27
Список рекомендуемой литературы ……………………………………….. 29
Приложения……………………………………………………………………. 30
Введение
Умение самостоятельно решать практические задачи по «Сопротивлению материалов» является важнейшим элементом усвоения этой дисциплины и во многом определяет способность студента принимать правильные решения в тех случаях, когда основными критериями работоспособности создаваемых или исследуемых инженерных конструкций являются прочность, жесткость и устойчивость.
Методические указания, включенные в сборник, предназначены для выполнения студентами индивидуальных заданий в различных формах – расчетно-проектировочных работ (РПР), расчетно-графических работ (РГР), технических расчетов (ТР), домашних заданий (ДЗ), контрольных и курсовых работ (КР) и пр. – в зависимости от предусмотренного вида самостоятельной работы студента при односеместровом и двухсеместровом курсах изучения дисциплины «Сопротивление материалов» как самостоятельного предмета или как раздела дисциплин «Механика», «Прикладная механика» и др. Предложенные методические указания носят характер самых общих рекомендаций по решению заданий и предполагают использование основной, вспомогательной и справочной литературы, а также конспектов лекций и упражнений по «Сопротивлению материалов».
Перечень из 12 задач, приведенных в этом сборнике, охватывает следующие темы курса:
1. Геометрические характеристики поперечных сечений бруса.
2. Расчет конструкций на прочность и жесткость при растяжении (сжатии).
3. Расчет бруса на прочность и жесткость при кручении.
4. Расчет балки на прочность и жесткость при изгибе.
5. Расчет статически неопределимой плоской рамы.
6. Расчеты при комбинированных видах нагружения (сложное сопротивление).
7. Расчет на устойчивость прямолинейного сжатого стержня.
8. Расчеты конструкций при динамическом нагружении.
Содержание выполняемых заданий соответствуют принятым рабочим программам подготовки студентов. Состав заданий (перечень задач в каждом из заданий) утверждается решениями ведущей кафедры и доводится до сведения студентов преподавателем.
Структура методических указаний состоит из:
- текстов задач по основным разделам курса и таблиц числовых данных параметров, выбор которых зависит от индивидуального буквенно-цифрового шифра студента;
- вариантов расчетных схем к задачам;
- кратких методических указаний по выполнению заданий;
- приложений, необходимых для решения задач.
ОБЩИЕ УКАЗАНИЯ
Каждый студент очно-заочной или заочной формы обучения выполняет то количество контрольных заданий (РПР, РГР, ДЗ, ТР, КР и др.), которое предусмотрено учебным планом его специальности (или направления подготовки) и соответствующей рабочей программой. Номера задач, входящих в состав контрольных заданий в зависимости от их запланированного количества в рабочей программе и формы обучения, представлены в табл. 1.
Таблица 1
| Вид контрольных заданий | Номер контрольного задания | Номера задач в контрольных заданиях | |||||||
| Формы обучения | |||||||||
| Очно-заочная (вечерняя) | Заочная | ||||||||
| Количество контрольных заданий | Количество контрольных заданий | ||||||||
| одно | два | три | четыре | одно | два | три | четыре | ||
| Технический расчет (ТР) | № 1 | 1,2 | 1,2 | 1,2 | 1,2 | 1,3 | 1,3 | 1,3 | 1,3 |
| № 2 | – | 3,4 | 3,4 | 3,4 | – | 3,5 | 3,5 | 3,5 | |
| № 3 | – | – | 5,7 | 5,7 | – | – | |||
| № 4 | – | – | – | – | – | – | |||
| Домашнее задание (ДЗ) | № 1 | 1,2 | 1,2 | 1,2 | 1,2 | 1,3 | 1,3 | 1,3 | 1,3 |
| № 2 | – | 3,4 | 3,4 | 3,4 | – | 3,5 | 3,5 | 3,5 | |
| № 3 | – | – | 5,7 | 5,7 | – | – | |||
| № 4 | – | – | – | – | – | – | |||
| Расчетно-проектировочная работа (РПР) | № 1 | 1,2,3,5 | 1,2,3,5 | 1,2,3 | 1,2,3 | 1,2,3,5 | 1,2,3,5 | 1,2,3 | 1,2,3 |
| № 2 | – | 6,7,9 | 5,6,7 | 5,6,7 | – | 6,7,9 | 5,6,7 | 5,6,7 | |
| № 3 | – | – | 9,10 | 9,10 | – | – | 9,10 | 9,10 | |
| № 4 | – | – | – | 11,12 | – | – | – | 11,12 | |
| Расчетно-графическая работа (РГР) | № 1 | 1,2,3,5 | 1,2,3,5 | 1,2,3 | 1,2,3 | 1,2,3,5 | 1,2,3,5 | 1,2,3 | 1,2,3 |
| № 2 | – | 6,7,9 | 5,6,7 | 5,6,7 | – | 6,7,9 | 5,6,7 | 5,6,7 | |
| № 3 | – | – | 9,10 | 9,10 | – | – | 9,10 | 9,10 | |
| № 4 | – | – | – | 11,12 | – | – | – | 11,12 | |
| Контрольная работа | № 1 | 1,2,3,4 | 1,2,3,4 | 1,2,3 | 1,2,3 | 1,2,3,4 | 1,2,3,4 | 1,2,3 | 1,2,3 |
| № 2 | – | 6,9,10 | 4,6,7 | 4,6,7 | – | 5,6,10 | 5,6,7 | 5,6,7 | |
| № 3 | – | – | 9,10 | 9,10 | – | – | 9,10 | 9,10 | |
| № 4 | – | – | – | 11,12 | – | – | – | 11,12 | |
| Курсовая работа (КР) | № 1 | 1,2,3,5,9 | 1,2,3,5 | – | – | 1,2,3,6,9 | 1,2,3,6 | – | – |
| № 2 | – | 9,10,11 | – | – | – | 9,10,12 | – | – |
Примечание. В случае необходимости или изменения учебных планов кафедра имеет право вносить изменения или дополнения в перечень заданий. Если при этом число задач или их темы выходят за рамки настоящих указаний, следует воспользоваться методическими указаниями [6].
Исходные данные для каждой задачи определяются шифром - номером зачетной книжки студента, которому поставлены в соответствие пять букв русского алфавита. Например: № зачетной книжки студента – 93052; тогда
цифры шифра– 9 3 0 5 2;
соответствующие буквы шифра – б в г д е.
Из каждого вертикального столбца таблицы, обозначенного внизу определенной буквой шифра, надо взять только одно число, стоящее в той горизонтальной строке, номер которой совпадает с номером буквы шифра.
ЗАДАЧИ КОНТРОЛЬНЫХ ЗАДАНИЙ
VI VII VIII IX X
 |
 |
 |
 |
 |
 |
 |
Рис. 1
IV V
 |
 |
 |
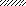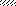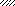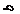
A A
 |
 |
 |
2A b c 2A Q
Q
a b
VI VII VIII
 |
 |
 |
 |
 |
 |
 |
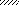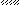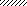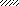| A |
с a b b c a b b a c
IX X
 |
 |
 |
 |
 |
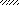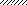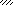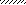A 2A Q 2A A A Q
a c b c b a
Рис.2
Указания. Для определения двух неизвестных усилий в стержнях следует совместно решить уравнение статики и уравнение совместности деформаций.
Для ответа на третий вопрос задачи следует иметь в виду, что в одном из стержней напряжение может быть больше, чем в другом. При увеличении нагрузки напряжение в этом стержне достигнет предела текучести раньше, чем во втором. Для идеально пластичного материала дальнейший рост напряжений в этом стержне прекращается, и усилие растяжения в нем становится постоянным N1пред = σт⋅A1. При дальнейшем увеличении нагрузки достигается предел текучести и в другом стержне (N2пред = σт⋅A2). Подставив в уравнение статики предельные значения усилий в стержнях, найдем из него предельную грузоподъемность Qпр, а затем и допускаемую нагрузку Qдоп.
I VI
M1 M2 M3 X M1 M2 M3 X
II VII
VII
M1 M2 M3 X
M1 M2 M3 X M1 M2 M3 X
III VIII
M1 M2 M3 X
VIII
M1 M2 M3 X
M1 M2 M3 X M1 M2 M3 X
IV IX
M1 M2 M3 X
M1 M2 M3 X M1 M2 M3 X
V X
M1 M2 M3 X
X
d b c e b c e d
a b c a
Рис. 3
Q P q
X
M
a3 a3 P a3 a3 a2
l1 = 10a l2 = 10a
Рис. 4. Окончание
Задача 5.Для балки, изображенной на рис. 5, требуется:
1) найти изгибающий момент на левой опоре (в долях ql2);
2) построить эпюры Q и M;
3) построить эпюру прогибов, вычислив три ординаты в пролете и две – на консоли.
Данные взять из табл. 6.
Указание. Жесткость при изгибе принять постоянной EJx для всех участков балки.
Таблица 6
| Цифра шифра | Схема по рис. 5 | α | β | Цифра шифра | Схема по рис. 5 | α | β | |
| 5 | I II III IV V | 0,1 0,2 0,3 0,4 0,5 | 0,1 0,2 0,3 0,4 0,5 | VI VII VIII IX X | 0,6 0,7 0,8 0,9 1,0 | 0,6 0,7 0,8 0,9 1,0 | ||
| Буква шифра | е | г | д | Буква шифра | е | г | д |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
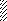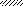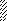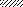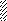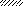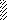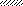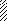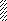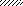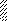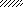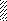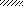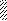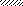P=αql
P=αql
II q VII q
q
VII
P=αql
q
P=αql
P=αql P=αql
q VIII P=αql q
III
P=αql
q P=αql
VIII
P=αql
P
P=αq
q P=αql q
IV IX
P=αql
P=αql P=αql P=αql
P=αql q q
V X
P=αql
l / 2 l / 2 β l l / 2 l / 2 β l
Рис. 5
Указания. Для ответа на первый вопрос нужно составить два уравнения:
1) уравнение статики в виде суммы моментов всех сил относительно правой опоры;
2) уравнение метода начальных параметров, учитывающее нулевой прогиб на правой опоре. Из этих двух уравнений можно найти реактивные момент и силу в заделке.
Для ответа на третий вопрос целесообразнее всего использовать метод начальных параметров, так как два начальных параметра (y0 и θ0) обращаются в ноль (при условии расположения начала координат в заделке), а два других (M0 и Q0) перед этим были найдены.
Косой изгиб.
Задача 7.
Для балки, работающей в условиях косого изгиба (рис.8), необходимо вычислить наибольшие нормальные напряжения в опасном сечении.
Указания. Положение опасного сечения по длине балки может быть выражено неявно. В этом случае опасное сечение определится в результате численного расчета нормальных напряжений в предполагаемых опасных сечениях.
Данные взять из табл.8, схему балки выбрать из рис. 7.
Таблица 8
| Цифра шифра | Схема по рис.8 | Р1, кН | Р2, кН | а, м | Поперечное сечение |
| 0,3 | № 20 | ||||
| 0,4 | № 20 | ||||
| 0,5 | № 30 | ||||
| 0,6 | № 24 | ||||
| 0,8 | № 30 | ||||
| 0,6 | № 40 | ||||
| 0,5 | № 24 | ||||
| 0,4 | № 18 | ||||
| 0,3 | № 16 | ||||
| 0,4 | № 40 | ||||
| Буква шифра | д | б | г | в | е |
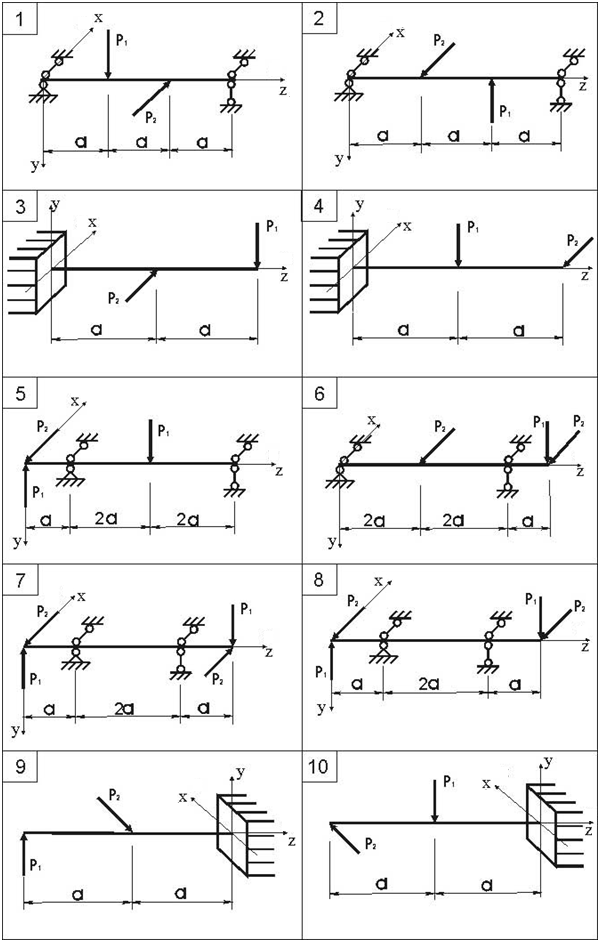
Рис. 7
Задача 8.
Колонна, поперечное сечение которой задано (см. рис.8), нагружена сжимающей силой Р, приложенной в точке А.
Требуется:
1) определить положение нейтральной линии в поперечных сечениях колонны;
2) определить наибольшие сжимающие и растягивающие напряжения;
3) построить плоскую эпюру нормальных напряжений.
Данные взять из табл.9, схему рамы выбрать из рис. 8.
Таблица 9
| Цифра шифра | Номер схемы | а, см | b, см | Р, кН |
| Буква шифра | г | е | в | б |
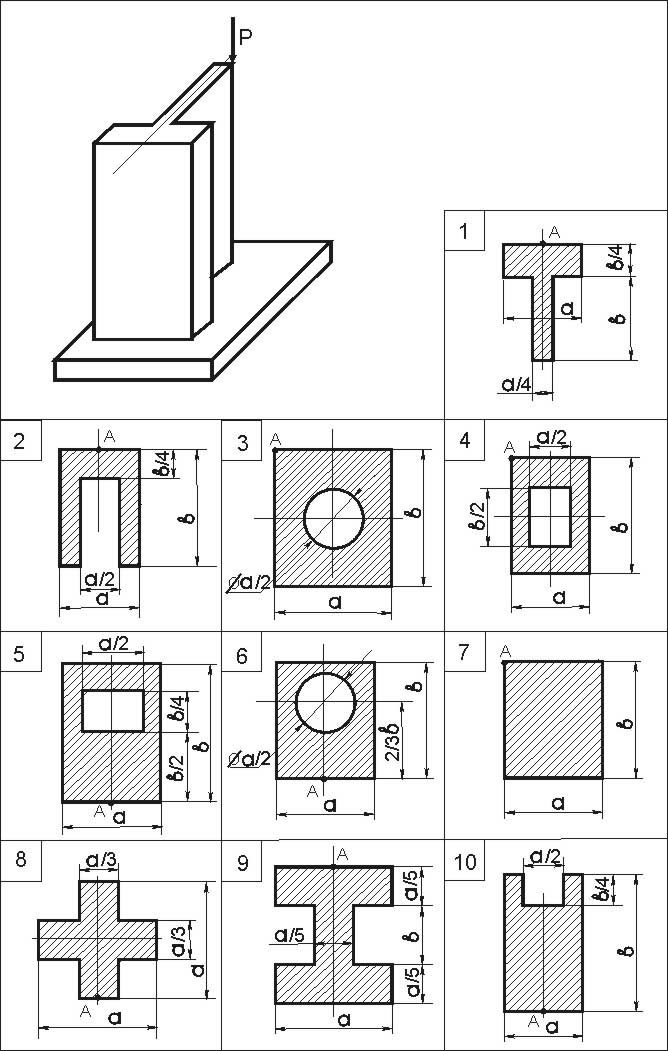
Рис. 8
Задача 9.
Стальной вал круглого поперечного сечения вращается со скоростью n об/мин и передаёт мощность N посредством зубчатого колеса с окружным усилием P и шкива, усилия в ведущей и ведомой ветвях которого соответственно равны 2t и t. Ветви ремня параллельны друг другу и наклонены к горизонту под углом α, а окружное усилие действует под углом β.
Требуется:
1) Разложив окружное усилие P и усилия 2t и t ветвей ремня на составляющие в вертикальной и горизонтальной плоскостях, изобразить аксонометрическую расчётную схему вала и указать на ней все внешние силы и моменты (включая предполагаемые реакции связей в опорах);
2) Из уравнений равновесия рассчитать реакции связей в опорах;
3) Построить эпюры изгибающих и крутящих моментов для вала;
4) Установить опасное сечение вала и определить его диаметр d, используя четвёртую теорию прочности.
Данные для решения взять из табл. 10, схему вала – из рис. 9.
Таблица 10
| Цифра шифра | Номер схемы | N, кВт | n, об/мин | D1, м | а, м | α, град | β, град | [ σ ], МПа |
| 0,4 | 0,25 | |||||||
| 0,35 | 0,3 | |||||||
| 0,5 | 0,4 | |||||||
| 0,35 | 0,2 | |||||||
| 0,4 | 0,15 | |||||||
| 0,3 | 0,2 | |||||||
| 0,6 | 0,25 | |||||||
| 0,3 | 0,35 | |||||||
| 0,4 | 0,4 | |||||||
| 0,3 | 0,2 | |||||||
| Буква шифра | д | е | г | д | в | е | г | б |
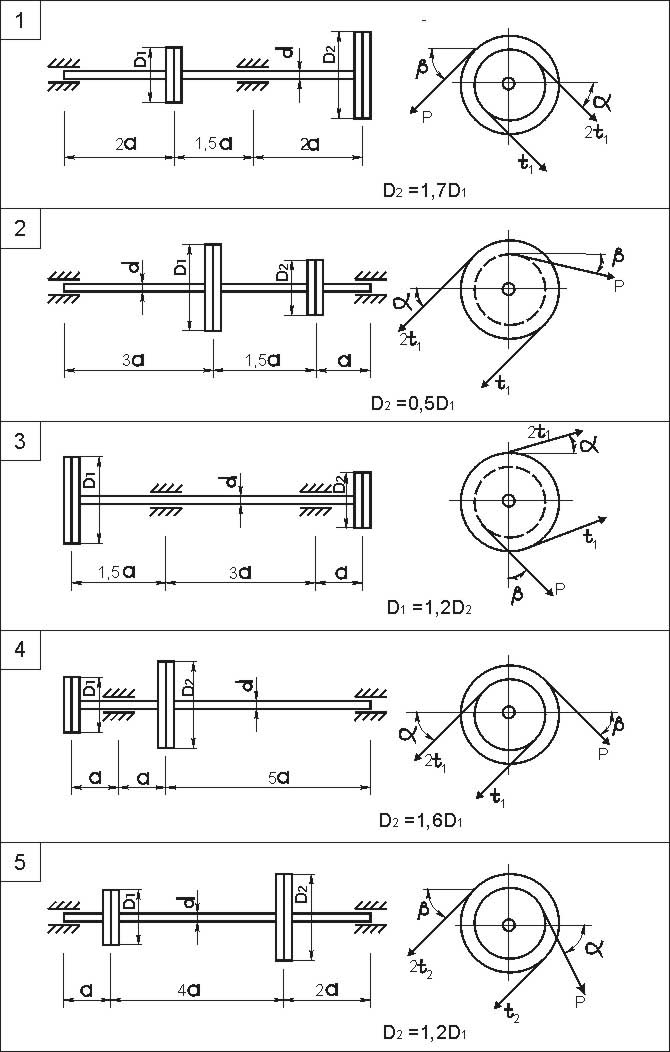
Рис. 9
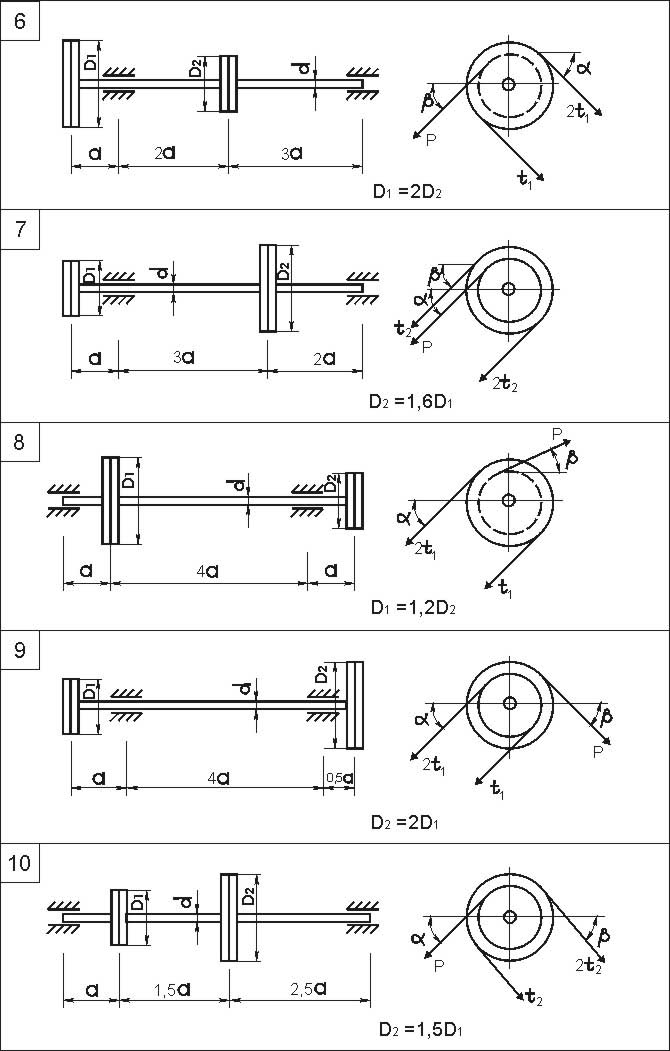
Рис. 9. Окончание
Тема № 7. Расчёт на устойчивость прямолинейного сжатого стержня.
Задача 10.Для стержня заданного сечения, нагруженной продольной силой Р требуется определить:
1) критическую силу Ркр, используя формулу Эйлера или формулу Ясинского;
2) допускаемую нагрузку Рдоп, используя метод расчёта с помощью коэффициента продольного изгиба φ;
3) коэффициент запаса устойчивости стойки;
Данные для решения взять из табл. 11, схему стержня – из рис. 10.
Указания:
1) стержни изготовлены из стали 3 (допускаемое напряжение при сжатии [σс] = 160 МПа);
2) коэффициенты в формуле Ясинского следует принять следующими:
| материал | а, МПа | b, МПа |
| Сталь 3 | 1,14 |
3) значения коэффициента φ продольного изгиба даны в приложении 4.
4) в случае, когда гибкость стержня λ >200, длину стержня следует уменьшить так, чтобы его гибкость стала меньше 200.
Таблица 11
| Цифра шифра | Схема по рис. 10 | Равнополочный уголок | Неравнополочный уголок | Швеллер | d, см | ℓ, м |
| 80х80х8 | 75х50х5 | № 12 | 3,8 | |||
| 160х160х12 | 100х63х10 | № 20 | 4,6 | |||
| 90х90х80 | 63х40х8 | № 14 | ||||
| 140х140х10 | 110х70х8 | № 24 | 4,8 | |||
| 100х100х12 | 80х50х6 | № 10 | 2,5 | |||
| 110х110х8 | 140х90х10 | № 18 | 3,2 | |||
| 125х125х12 | 100х63х8 | № 16 | 2,2 | |||
| 70х70х8 | 125х80х10 | № 22а | ||||
| 160х160х16 | 160х100х10 | № 20а | 4,2 | |||
| 180х180х18 | 180х110х10 | № 24 | 5,2 | |||
| Буква шифра | е | д | г | в | б | е |
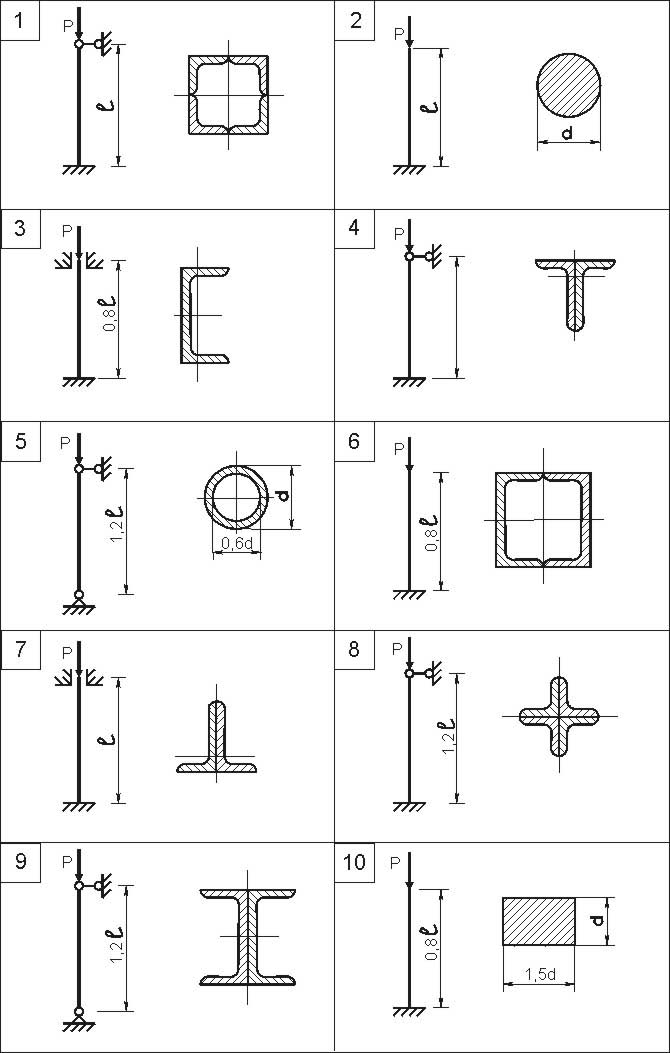
Рис.10
Список рекомендуемой литературы
а) основная литература:
1. Александров, А.В.
Сопротивление материалов : Учебник для вузов / А. В. Александров, В. Д. Потапов, Б. П. Державин. - 3-е изд., испр. - М. : Высш. шк., 2003. - 560с.
2. Агамиров, Л.В.
Сопротивление материалов: Краткий курс. Для студентов вузов / Л. В. Агамиров. - М. : АСТ, 2003. - 256с.
3. Беляев, Н.М.
Сопротивление материалов / Н. М. Беляев. - 15-е изд.,перераб. - М. : Наука, 1976. - 607с.
4. Буланов, Э.А.
Решение задач по сопротивлению материалов : Учеб.пособие / Э. А. Буланов. - 2-е изд., испр. - М. : БИНОМ. Лаборатория знаний, 2005. - 207с.
5. Варданян, Г.С.
Сопротивление материалов (с основами строительной механики) : Учебник для вузов (МО) / Г. С. Варданян, Н. М. Атаров, А. А. Горшков. - М. : ИНФРА-М, 2003. - 480с. : ил. - 99-88.
6. Дарков А.В.,Шпиро Г.С.
Сопротивление материалов : Учебник / Дарков А.В.,Шпиро Г.С. - 4-е изд.,перераб. - М. : Высшая школа, 1975. - 654с.
7. Дарков А.В.,Шпиро Г.С.
Сопротивление материалов : Учебник / Дарков А.В.,Шпиро Г.С. - М. : Высшая школа, 1969. - 734с.
8. Кочетов, В.Т.
Сопротивление материалов / В. Т. Кочетов, А. Д. Павленко, М. В. Кочетов. - 2-е изд.,перераб.и доп. - Ростов-на-Дону : Феникс, 2001. - 368с.
9. Сборник задач по сопротивлению материалов : Учебн.пособие для втузов / Под ред.А.С.Вольмира. - М. : Наука, 1984. - 408с.
10. Степин, П.А.
Сопротивление материалов : Учебник для вузов / П. А. Степин. - 7-е изд. - М. : Высшая школа, 1983. - 303с.
б) дополнительная литература:
1.Сборник задач по сопротивлению материалов : Учебн. пособие для втузов / Под ред. А.С.Вольмира. - М. : Наука, 1984. - 408с.
2. Фесик, С.П. Справочник по сопротивлению материалов / С. П. Фесик. - Киев, 1982. - 280с.
3. Ицкович, Г.М.
Руководство к решению задач по сопротивлению материалов : Учеб.пособие / Г. М. Ицкович. - М. : Высшая школа, 1970. - 542с.
4. Пособие к решению задач по сопротивлению материалов : Учебное пособие для ВТУЗов / И.Н.Миролюбов,С.А.Енгалычев,Н.Д.Сергиевский и др. - 4-е изд.,перераб. - М. : Высшая школа, 1974. - 392с.
5. Писаренко, Г.С.
Справочник по сопротивлению материалов / Г. С. Писаренко, А. П. Яковлев, А. П. Матвеев. - 2-е изд.,перераб. и доп. - Киев : Наукова думка, 1988- 736с.
6. Сопротивление материалов: Метод.указания и задания для выполнения РПР / Сост.Г.С.Мадорский,А.В.Терновой. - Ковров : КГТА, 1997. - 52с.
в) программное обеспечение:
компьютерные программы: серия видеофильмов «Сопротивление материалов в примерах решения задач» (автор А.В. Терновой – http//:aem.ucoz.ru), видео презентация «Вспомним сопротивление материалов» (автор А.В. Терновой).
Основные формулы курса «Сопротивление материалов» можно найти на сайте http//:www.svkspb.nm.ru
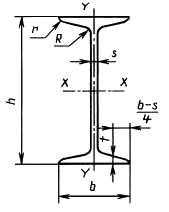Приложение 1
Приложение 2
Приложение 3
Приложение 4
Таблица коэффициентов продольного изгиба φ
Гибкость 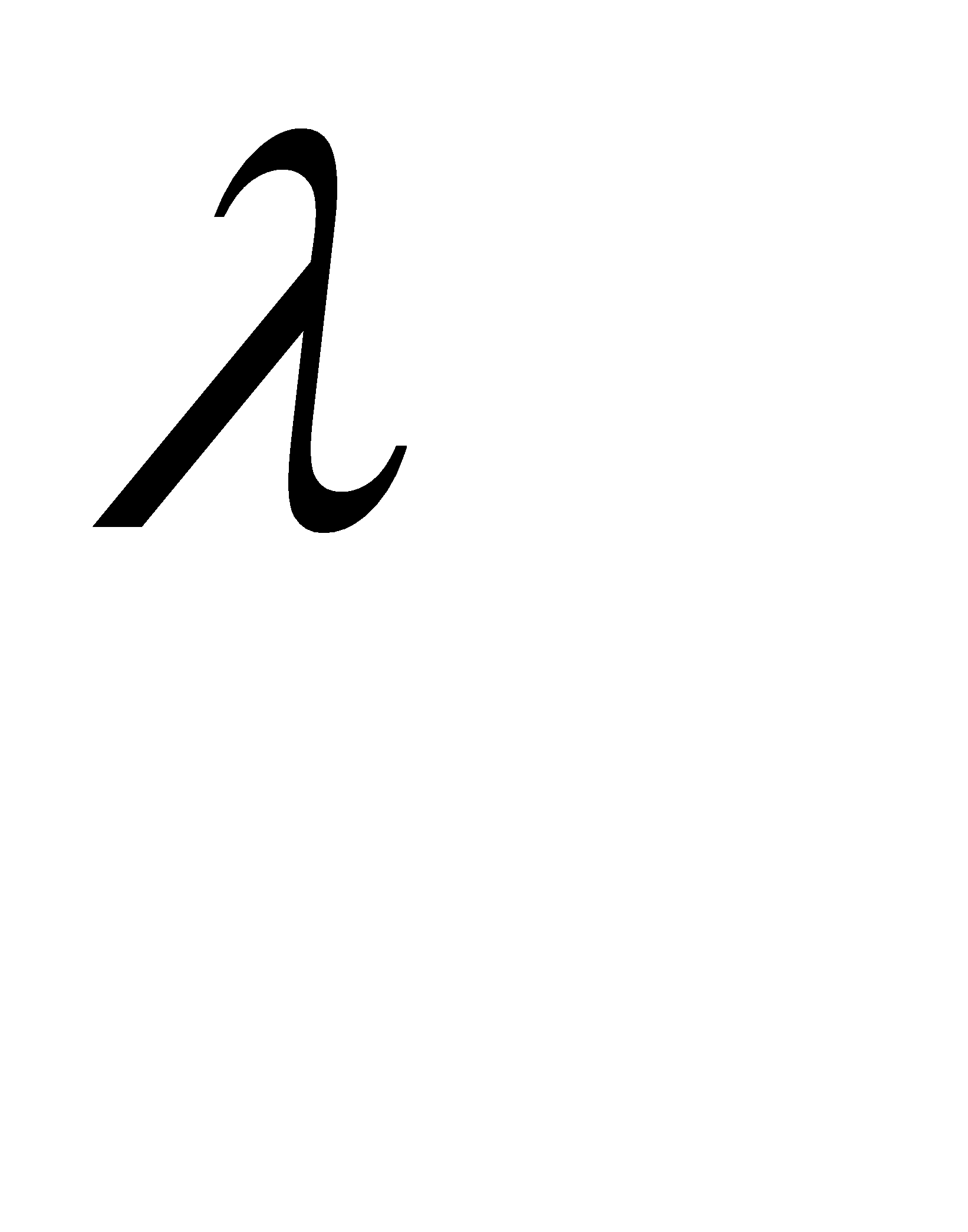 | Значения коэффициента φ | ||||||
| Для сталей с приведенными расчетными сопротивлениями [σ], МПа | |||||||
| 0,988 | 0,987 | 0,985 | 0,984 | 0,983 | 0,982 | 0,981 | |
| 0,967 | 0,962 | 0,959 | 0,955 | 0,952 | 0,949 | 0,946 | |
| 0,939 | 0,931 | 0,924 | 0,917 | 0,911 | 0,905 | 0,900 | |
| 0,906 | 0,894 | 0,883 | 0,873 | 0,863 | 0,854 | 0,846 | |
| 0,869 | 0,852 | 0,836 | 0,822 | 0,809 | 0,796 | 0,785 | |
| 0,827 | 0,805 | 0,785 | 0,766 | 0,749 | 0,721 | 0,696 | |
| 0,782 | 0,754 | 0,724 | 0,687 | 0,654 | 0,623 | 0,595 | |
| 0,734 | 0,868 | 0,641 | 0,602 | 0,566 | 0,532 | 0,501 | |
| 0,665 | 0,612 | 0,565 | 0,522 | 0,483 | 0,447 | 0,413 | |
| 0,599 | 0,542 | 0,493 | 0,448 | 0,408 | 0,369 | 0,335 | |
| 0,537 | 0,478 | 0,427 | 0,381 | 0,338 | 0,306 | 0,280 | |
| 0,479 | 0,419 | 0,366 | 0,321 | 0,287 | 0,260 | 0,237 | |
| 0,425 | 0,364 | 0,313 | 0,276 | 0,247 | 0,223 | 0,204 | |
| 0,376 | 0,315 | 0,272 | 0,240 | 0,215 | 0,195 | 0,178 | |
| 0,328 | 0,276 | 0,239 | 0,211 | 0,189 | 0,171 | 0,157 | |
| 0,290 | 0,244 | 0,212 | 0,187 | 0,167 | 0,152 | 0,139 | |
| 0,259 | 0,218 | 0,189 | 0,167 | 0,150 | 0,136 | 0,125 | |
| 0,233 | 0,196 | 0,170 | 0,150 | 0,135 | 0,123 | 0,112 | |
| 0,210 | 0,177 | 0,154 | 0,136 | 0,122 | 0,111 | 0,102 | |
| 0,191 | 0,161 | 0,140 | 0,124 | 0,111 | 0,101 | 0,093 |
очно-заочной и заочной форм обучения
Составитель: А.В. Терновой
Ковров 2013
УДК 539.3/6
С
Сопротивление материалов: Контрольные задания и методические указания для студентов заочного отделения [Текст]: / Сост.: А.В. Терновой А.В. – Ковров: ФГБОУ ВПО «КГТА им. В.А.Дегтярева»,2013.– 35 с.
Контрольные задания и методические указания для студентов очно-заочного и заочного отделения направлен на получение студентами практических навыков в самостоятельном решении задач по дисциплинам «Сопротивление материалов», а также по таким дисциплинам, как «Механика», «Прикладная механика», в которых рассматривается разделы курса "Сопротивление материалов".
Перечень представленных задач охватывает наиболее важные разделы дисциплины «Сопротивление материалов» и является универсальным при формировании структуры и содержания самостоятельной работы студентов всех специальностей, направлений (профилей) очно-заочной и заочной форм обучения, для которых эта дисциплина или ее разделы предусмотрены федеральными государственными образовательными стандартами и принятыми рабочими программами.
Табл.13 . Ил.12 , Библиогр.: 16 назв.
Рецензенты:
ISBN ////////////////////////
ОГЛАВЛЕНИЕ
Стр.
Введение …………………………………………………………………… 4
Общие указания…………………………………………………………… 4
Задачи контрольных заданий…………………………………………… 7