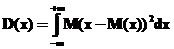Равномерная функция распределения
Пусть х принимает значение от а до в
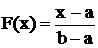 , т.к.
, т.к. 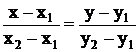
 F(x)
F(x)

 1- равномернаая функция распределе-
1- равномернаая функция распределе-
ния.
 а b x
а b x
Тогда f(x):
 f(x)
f(x)

 1
1
 f(x)=
f(x)= 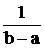
 a b
a b
 Нормальное распределение
Нормальное распределение
F(x)

 1- 1
1- 1
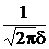

 0,5
0,5

 a x x
a x x
a,d -параметры
функции распределения: 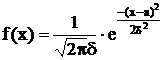
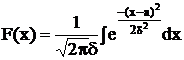
Биноминальное распределение
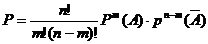
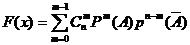
Закон распеределения Пуассона
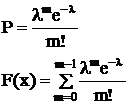
Числовые характеристики случайных величин
В расчетах надежности
В расчетах надежности часто используют числовые характеристики случайных величин, которые выражают наиболее существенные законы распределения.
Для оценки среднего (в вероятностном понимании) значения случайной величины вводят понятие математического ожидание.
Математическое ожидание – это действительное среднее значение случайной величины и определяется оно с учетом вероятностей отдельных ее значений.
Для дискретной случайной величины математическое ожидание М(х)
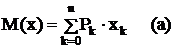
Для непрерывной случайной величины:
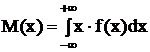
Для равновероятных событий:
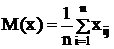
Основные теоремы математического ожидания случайной величины
1. Математическое ожидание постоянной величины равно этой постоянной величине
М(с) = с
эта теорема получается из формулы А
2. Математическое ожидание алгебраической суммы любых случайных величин равно сумме математических ожиданий этих случайных величин.
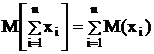
3. Математическое ожидание произведения независимых случайных величин равно произведению математических ожиданий этих случайных величин:
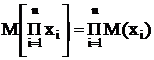
4. Математическое ожидание произведения постоянной величины с на случайную величину х равно произведению этой постоянной величины на математическое ожидание случайной величины:
М(с×х) = с×М(х)
5. Математическое ожидание произведения 2-х случайных зависимых величин равно произведению математических ожиданий этих величин плюс корелляционный момент:
М(ху) = М(х)×М(у)+кху
6. Математическое ожидание линейной функции равно линейной функции от этого математического ожидания:
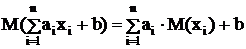
Пример:
Найдем выражение математического ожидания для равномерного закона распределения.
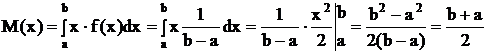
Математическое ожидание случайной величины характеризует ее действительное значение, но этого недостаточно для полной оценки случайной величины. Необходимо еще знать насколько в среднем случайная величина отклоняется от статистического среднего значения, т.е. от математического ожидания.
Для количественной оценки отклонения случайной величины от математического ожидания принимают величину, которая равна математическому ожиданию квадрата отклонения случайной величины от ее математического ожидания и эта величина называется дисперсией случайной величины х.
D(х) = М(х – М(х))2
Квадратный корень из величины дисперсии называется среднеквадратическим отклонением случайной величины.
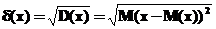
Для дискретной случайной величины дисперсия равна:
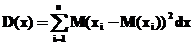
Для непрерывной случайной величины: