Расчет уровней значимости коэффициентов корреляции
Все коэффициенты корреляции, которые будут рассмотрены ниже, не имеют стандартных таблиц для нахождения критических значений. В этих случаях поиск критических значений осуществляется с помощью t-критерия Стьюдента по формуле (11.9).
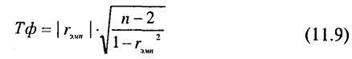
где tэмп — коэффициент корреляции, п — число коррелируемых признаков, а величина Тф проверяется на уровень значимости по таблице 16 Приложения 1 для t-критерия Стьюдента. Число степеней свободы в этом случае будет равно k = п — 2.
Однако с помощью формулы (11.9) можно проводить оценку уровней значимости и коэффициентов корреляции Пирсона и Спирмена. Проведем, в частности, проверку уровня значимости коэффициента корреляции, полученного при решении задачи 11.3 и равного — 0,82. Мы помним, что он попал в зону неопределенности, согласно таблице 21 Приложения 1. Вычисляем уровень значимости этого коэффициента по формуле 11.9:
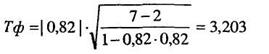
Число степеней свободы k= п - 2; в нашем случае при п = 7, k= 7 - 2 = 5. По таблице 16 Приложения 1 находим критические значения критерия Стьюдента, они равны соответственно для Р≤ 0,05 tкр = 2,57 и для Р≤ 0,01 tкр = 4,03. В принятой форме записи это выглядит так:
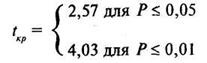
Строим «ось значимости»:
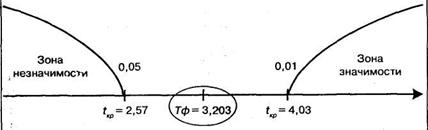
Полученная величина Тф, как и в случае решения задачи 11.3, попала в зону неопределенности.
11.5. Коэффициент корреляции «φ»
При сравнении двух переменных, измеренных в дихотомической шкале, мерой корреляционной связи служит так называемый коэффициент «φ», или, как назвал эту статистику ее автор К. Пирсон, — «коэффициент ассоциации».
Величина коэффициента «φ» лежит в интервале +1 и -1. Он может быть как положительным, так и отрицательным, характеризуя направление связи двух дихотомически измеренных признаков.
Решим с помощью коэффициента корреляции «φ» следующую задачу.
Задача 11.5 Влияет ли семейное положение на успешность учебы студентов-мужчин?
Решение. Для решения этой задачи психолог выясняет у 12 студентов-мужчин, во-первых, женат он или холост, соответственно проставляя каждому 1 — женат или 0 — холост, и, во-вторых, насколько успешно тот учится: успешной учебе проставляется код 0, при наличии академических задолженностей проставляется код 1. Для решения данные лучше свести в таблицу 11.6.
Таблица 11.6
| №п/п | X — семейное положение: 0 — холост, 1 — женат | Y — успешность обучения неуспешно — 1, успешно — 0 |
В общем виде формула вычисления коэффициента корреляции φэмп выглядит так:
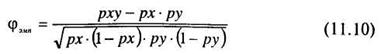
где рх— частота или доля признака, имеющего 1 по X, (1 - рх)— доля или частота признака, имеющего 0 по X; ру — частота или доля признака, имеющего 1 по Y, (1 - ру)— доля или частота признака, имеющего 0 по Y, рху — доля или частота признака, имеющая 1 одновременно как по X так и по Y
Частоты вычисляется следующим образом: подсчитывается количество 1 в переменной X и полученная величина делится на общее число элементов этой переменной — N. Аналогично подсчитываются частоты для переменной Y. Обозначение рху— соответствует частоте или доле признаков, имеющих единицу как по X так и по Y.
Возвращаемся к решению задачи 11.5. Пусть рхсоответствует доле студентов, имеющих 1 по X, тогда рх = 5/12= 0,4167 (пять единичек, поделенных на общее число студентов, принявших участие в эксперименте). В этом случае (1 - рх) = 1 - 0,4167 = 0,5833. Пусть обозначение ру — соответствует доле студентов, имеющих 1 по Y, тогда ру= 6/12 = 0,5. В этом случае (1 - ру) = 1 — 0,5 = 0,5.
Подсчитаем рху— долю студентов, имеющих единицу как по Х так и по Y. В нашем случае рху = 4/12 = 0,3333.
Подставляем полученные величины в формулу (11.10), получаем
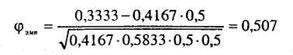
Поскольку, как мы уже указывали выше, для этого коэффициента корреляции нет таблиц значимости, рассчитываем его значимость по формуле (11.9).
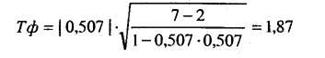
Число степеней свободы в нашем случае будет равно
k = п - 2 = = 12 — 2 = 10. По таблице 16 Приложения 1 для k = 10 находим критические значения критерия Стьюдента, они равны соответственно для Р ≤0,05 tкр = 2,23 и для Р ≤ 0,01 tкр= 4,59. В принятой форме записи это выглядит так:
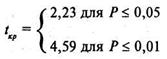
Строим «ось значимости»:
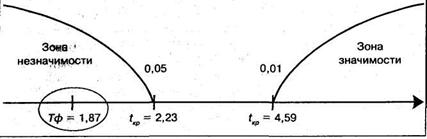
Значение величины Тф попало в зону незначимости. Иными словами, психолог не обнаружил никакой связи между успешностью обучения и семейным положением студентов. Или, в терминах статистических гипотез, гипотеза Н1 отклоняется и принимается гипотеза Но о сходстве коэффициента корреляции «φ» с нулем.
Отметим, что кодирование, т.е. приписывание чисел 0 или 1 тому или иному признаку, было произвольным. Можно было проставить холостым 1, значение коэффициента «φ» при этом не изменилось бы. Проверьте!
11.5.1. Второй способ вычисления коэффициента «φ»
Коэффициент «φ» можно вычислить, не применяя метод кодирования. В этом случае используется так называемая четырехпольная таблица, или таблица сопряженности. Каждую клетку таблицы обозначим соответствующими буквами a, b, с и d. Используя эту таблицу, решим задачу 11.5, приведенную в предыдущем разделе. Представим данные этой задачи в виде таблицы 11.7.
Таблица 11.7
| Значение признаков | Семейное положение | Сумма | |
| Холостые | Женатые | ||
| Плохо учится | а = 2 | b = 4 | |
| Учится хорошо | с = 5 | d = 1 | |
| Сумма |
В каждой клетке таблицы 11.7 приведено число студентов, обладающих сразу двумя характеристиками. Например в верхней левой клетке, имеющей обозначение а, указано общее число студентов, которые одновременно являются холостыми и имеют плохую успеваемость. Подобных студентов было обнаружено 2 человека. Таким же способом заполняют все клетки таблицы.
Приведем общую формулу расчета коэффициента «φ» по таблице сопряженности:
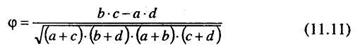
Подставляем данные таблицы 11.7 в формулу 11.11, получаем:
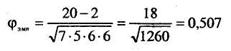
Значение φэмп, как этого следовало ожидать, получилось то же самое, что и в предыдущем случае. Поскольку мы уже оценили уровень значимости, второй раз этого делать не стоит.
Для применения коэффициента корреляции «φ» необходимо соблюдать следующие условия:
1.Сравниваемые признаки должны быть измерены в дихотомической шкале.
2.Число варьирующих признаков в сравниваемых переменных X и Y должно быть одинаковым.
3. Для оценки уровня достоверности коэффициента «φ» следуетпользоваться формулой (11.9) и таблицей критических значений для t-критерия Стьюдента при k = п - 2.
11.6. Коэффициент корреляции «τ» Кендалла
Коэффициент корреляции «τ» (тау) Кендалла относится к числу непараметрических, т.е. при вычислении этого коэффициента не играет роли характер распределения сравниваемых переменных. Коэффициент «τ» предназначен для работы с данными, полученными в ранговой шкале. Иногда этот коэффициент можно использовать вместо коэффициента корреляции Спирмена, поскольку способ его вычисления более прост. Он основан на вычислении суммы инверсий и совпадений.
Решим следующую задачу, применяя коэффициент «τ».
3адача 11.6 Психолог просит супругов проранжировать семь личностных черт, имеющих определяющее значение для семейного благополучия. Задача заключается в том, чтобы определить, в какой степени совпадают оценки супругов по отношению к ранжируемым качествам.
Данные задачи и необходимые для вычислений коэффициента Кендалла столбцы представим сразу в виде таблицы 11.8:
Таблица 11.8
| Черты личности | Муж | Жена | Совпадения | Инверсии |
| Ответственность | ||||
| Общительность | ||||
| Сдержанность | ||||
| Выносливость | ||||
| Жизнерадостность | ||||
| Терпеливость | ||||
| Решительность | ||||
| Сумма |
Для подсчета коэффициента корреляции «τ» (тау) необходимо упорядочить второй столбец (оценки мужа) таблицы 11.8 по возрастанию рангов, в нашем случае от 1 до 7. Соответственно этому поменяются местами как сами черты, так и соответствующие ранги третьего ряда. Оформим эти преобразования в новую таблицу 11.9:
Таблица 11.9
| № 1 | № 2 | № 3 | №4 | № 5 |
| Черты личности | Муж | Жена | Совпадения | Инверсии |
| Общительность | ||||
| Выносливость | ||||
| Сдержанность | ||||
| Терпеливость | ||||
| Жизнерадостность | ||||
| Отзывчивость | ||||
| Ответственность | ||||
| Сумма |
Посмотрим, как следует заполнять последние два столбца таблицы 11.9. Теперь для работы нам нужен только столбец с рангами, проставленными женой. На его основе заполним последние два столбца таблицы 11.9, подсчитав, сначала число совпадений.
Подсчет совпадений происходит следующим образом: берем самое верхнее число третьего столбца — 5. Подсчитываем сколько всего чисел больших 5 встречаются ниже в этом же столбце. Находим их — это 6 и 7. Их всего два. Двойку ставим напротив числа 5 в колонке «Совпадения». Берем затем следующее число 6 — ниже по столбцу и больше его, также ниже по столбцу, встречается только одно число 7. Ставим напротив 6 в столбце «Совпадения» — 1. Берем следующее число 7 — больше по величине не может встретиться ни одно число, поскольку 7 это максимальный ранг. Ставим напротив 7 в столбце «Совпадения» — 0. И так далее.
Для определения количества инверсий опять берем самое верхнее число третьего столбца — 5. Подсчитываем, сколько всего чисел встречаются ниже по столбцу, меньших, чем 5. Это числа 4, 3, 2 и 1. Их 4. Ставим напротив числа 5 в столбце «Инверсия» число 4. Берем следующее число 6 — ниже по столбцу и меньше, чем 6, встречаются те же числа, что и для 5. Ставим напротив 6 в столбце «Инверсия» число — 4. То же верно и для числа 7. Меньше числа 3 ниже по столбцу встречаются числа 2 и 1. Ставим напротив 3 в столбце «Инверсия» число — 2. И так далее.
Число совпадений обозначается буквой Р, а число инверсий буквой Q. Для проверки правильности подсчета числа инверсий и совпадений используется следующая формула:

Где Р — число совпадений,
Q — число инверсий,
N-— число ранжируемых признаков (черт).
Подставляем в формулу (11.12) полученные в нашем случае величины, получаем:
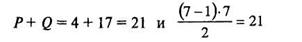
Следовательно, подсчет числа инверсий и совпадений был произведен правильно.
Подсчет коэффициента Кендалла может осуществляться по трем тождественным формулам. Первая формула:

В двух других формулах используются либо Р, либо Q:


Проведем подсчет коэффициента корреляции по всем трем формулам:
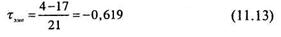
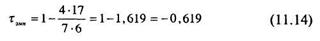
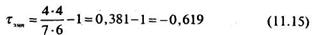
Проверим уровень значимости коэффициента корреляции по формуле (11.9):
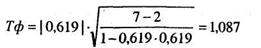
Число степеней свободы в нашем случае будет k= п - 2 = = 7 - 2 = 5. По таблице 16 Приложения 1 для к - 5 находим критические значения критерия Стьюдента, они равны соответственно для Р≤ 0,05 tкр = 2,57 и для P ≤ 0,01 tкр = 4,03. В, принятой форме записи это выглядит так:
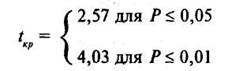
Строим «ось значимости»:
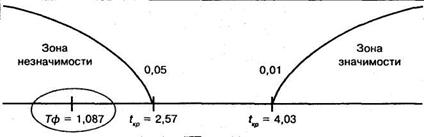
Значение величины Тф попало в зону незначимости. В терминах статистических гипотез гипотеза Н1 отклоняется и принимается гипотеза Но о том, что коэффициент корреляции «τ» Кендалла достоверно не отличается от нуля. Иными словами, согласованности между мужем и женой в оценке значимых для семейного благополучия личностных черт нет.
Для применения коэффициента корреляции «τ» Кендалла необходимо соблюдать следующие условия:
1. Сравниваемые признаки должны быть измерены в порядковой шкале.
2. Число варьирующих признаков в сравниваемых переменных X и Y должно быть одинаковым.
2.Величина «τ» Кендалла независима от закона распределения величин X и Y.
3.При расчетах этого коэффициента не допускается использование одинаковых рангов.
4.Для оценки уровня достоверности коэффициента «τ» следует пользоваться формулой (11.9) и таблицей критических значений для -критерия Стьюдента при k = п - 2.
