Парный критерий Т — Вилкоксона

Для решения задач, в которых осуществляется сравнение двух рядов чисел, кроме критерия знаков G психолог может использовать парный критерий Т— Вилкоксона. Этот критерий является более мощным, чем критерий знаков, и применяется для оценки различий экспериментальных данных, полученных в двух разных условиях на одной и той же выборке испытуемых. Он позволяет выявить не только направленность изменений, но и их выраженность, т.е. он позволяет установить, насколько сдвиг показателей в каком-то одном направлении является более интенсивным, чем в другом.

Критерий Т основан на ранжировании абсолютных величин разности между двумя рядами выборочных значений в первом и втором эксперименте (например «до» и «после» какого-либо воздействия). Ранжирование абсолютных величин означает, что знаки разностей не учитываются, однако в дальнейшем наряду с общей суммой рангов находится отдельно сумма рангов как для положительных, так и для отрицательных сдвигов. Если интенсивность сдвига в одном из направлении оказывается большей, то и соответствующая сумма рангов также оказывается больше. Этот сдвиг, как и в случае критерия знаков, называется типичным, а противоположный, меньший по сумме рангов сдвиг — нетипичным. Как и для критерия знаков эти два сдвига оказываются дополнительными друг к другу. Критерий Т — Вилкоксона базируется на величине нетипичного сдвига, который называется в дальнейшем Т_эмп

Задача 6.3.Психолог проводит с младшими школьниками коррекционную работу по формированию навыков внимания, используя для оценки результатов корректурную пробу. Задача состоит в том, чтобы определить, будет ли уменьшаться количество ошибок внимания у младших школьников после специальных коррекционных упражнений?

Решение. Для решения этой задачи психолог у 19 детей определяет количество ошибок при выполнении корректурной пробы до и после коррекционных упражнений. В таблице 6.5 приведены соответствующие экспериментальные данные и дополнительные столбцы, необходимые для работы по парному критерию Т — Вилкоксона.

Таблица 6.5

№ 1	№ 2	№ 3	№ 4	№ 5	№6	№7
№ испыту- емых п/п	До	После	Сдвиг (значение разности с учетом знака)	Абсолютные величины разностей	Ранги абсолютных величин разностей	Символ нетипичного сдвига
			-2		10,5
			- 1		6,5
			+ 1		6,5	*
			- 8
			- 11	и
			-20
			- 18
			- 1		6,5
			+ 1		6,5	*
			-22
			-1		6,5
			-2		10,5
			-6		13,5
			-4
			- 1		6,5
			+ 6		13,5	*
Сумма						Tэмп =26,5

Обработка данных по критерию Т — Вилкоксона осуществляется следующим образом:

1. В четвертый столбец таблицы 6.5 вносятся величины сдвигов с учетом знака. Их вычисляют путем вычитания из чисел третьего столбца соответствующих чисел второго столбца.

2. В пятом столбце в соответствие каждому значению сдвига ставят его абсолютную величину.

3. В шестом столбце ранжируют абсолютные величины сдвигов, представленных в пятом столбце.

4. Подсчитывают сумму рангов. В нашем примере она составляет:

12,5 + 6,5 + 6,5 + 15 + 16 + 2 + 18 + 17 + 6,5 + 6,5 + 19 + 6,5 + + 10,5 + 13,5 + 12 + 6,5 + 13,5 + 2 = 190

5. Подсчитывают сумму рангов по формуле (1.1):

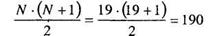
6. Проверяют правильность ранжирования на основе совпадения сумм рангов полученных двумя способами. В нашем случае обе величины совпали, 190 = 190, следовательно, ранжирование проведено правильно.

7. Любым символом отмечают все имеющиеся в таблице нетипичные сдвиги. В нашем случае — это три положительных сдвига.

8. Суммируют ранги нетипичных сдвигов. Это и будет искомая величина Т . В нашем случае эта сумма равна: Т = 6,5 + 13,5 + 6,5 = 26,5.

По таблице 2 Приложения определяют критические значения Т_кр для n = 19. Подчеркнем, что в данном критерии, в отличие откритерия знаков, поиск критических величин в таблице 2 Приложения ведется по общему числу испытуемых.

Нужная нам строка таблицы Приложения выделена ниже в таблицу 6.6:

Таблица 6.6

п	Р
0,05	0,01

Поскольку в нашем случае основной, типичный сдвиг — отрицательный, то дополнительный, «нетипичный» сдвиг будет положительным и на уровне значимости в 5% сумма рангов таких сдвигов не должна превышать числа 53, а при уровне значимости в 1% не должна превышать числа 38. Используем принятую форму записи, представим сказанное выше следующим образом:

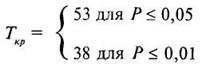
Строим «ось значимости»:

Анализ «оси значимости» показывает, что полученная величина Т_змп попадает в зону значимости. Можно утверждать, следовательно, что зафиксированные в эксперименте изменения неслучайны и значимы на 1% уровне. Таким образом, применение коррекционных упражнений способствует повышению точности выполнения корректурной пробы.

Полученный результат может быть переформулирован в терминах нулевой и альтернативной гипотез: поскольку преобладание типичного отрицательного направления сдвига в данном конкретном эксперименте не является случайным, то должна быть принята гипотеза H₁ о наличии различий, а гипотеза Н_о отклонена.

Обращаем внимание читателя, что направление «оси значимости» в этом критерии, так же как и критерии знаков, имеет положение нуля справа, в отличие от традиционного — слева, и увеличение числового ряда идет в противоположную сторону.

Для применения критерия Т Вилкоксона необходимо соблюдать следующие условия:

1. Измерение может быть проведено во всех шкалах, кроме номинальной.

2. Выборка должна быть связной.

3. Число элементов в сравниваемых выборках должно быть равным.

4. Критерий Т — Вилкоксона может применяться при численности выборки от 5 до 50 (на большую величину не рассчитана таблица достоверности).

Критерий Фридмана

Критерий Фридмана можно рассматривать как распространение критерия Т — Вилкоксона на три и большее количество измерений связной выборки испытуемых. Критерий позволяет установить уровень статистической достоверности различий сразу в нескольких измерениях (от 3 до 100), но не дает возможности выявить направление изменений. При наличии сразу нескольких измерений преимущество критерия Фридмана по сравнению с двумя предыдущими критериями очевидно, поскольку оба эти критерия работают только с двумя столбцами чисел. Предположим, что с помощью критерия знаков нам нужно было бы сравнить четыре столбца чисел. Тогда критерий знаков пришлось бы использовать шесть раз — сравнение первого столбца со вторым, третьим и четвертым, второго — с третьим и четвертым и третьего с четвертым. Критерий Фридмана позволяет выявить наличие значимых различий в измерениях за один раз.

Задача 6.4.Шести школьникам предъявляют тест Равена. Фиксируется время решения каждого задания. Выясняется вопрос — будут ли найдены статистически значимые различия между временем решения первых трех заданий теста?

Решение. Итак, психолог измерил время решения первых трех заданий теста у шести испытуемых.

Результаты этих измерений приведены в таблице:

Таблица 6.7

№ 1	№ 2	№ 3	№ 4
№ испытуемых п/п	Время решения первого задания теста в сек.	Время решения второго задания теста в сек.	Время решения третьего задания теста в сек.

Для нахождения различий можно было бы воспользоваться двумя предыдущими критериями, но тогда нужно было бы сравнивать между собой данные второго столбца с третьем и четвертым, а также данные третьего столбца с четвертым, т.е. выполнить три однотипных операции. Критерий Фридмана позволяет сразу сравнить между собой три и большее число столбцов, что дает возможность существенно ускорить процесс решения.

Применение критерия Фридмана требует выполнения следующих операций.

1. Ранжирование экспериментальных данных по строкамтаблицы 6.7. Обратите внимание, что в этом случае ранжирование проводится не по столбцам (вертикально), т.е. по одному показателю в группе испытуемых, а по строкам (горизонтально), т.е. по всем показателям для одного испытуемого. Выполняя эту операцию в нашей задаче, перепишем еще раз таблицу 6.7, добавив в нее необходимые столбцы для значений рангов.

Таблица 6.8

№ 1	№ 2	№ 3	№4	№ 5	№ 6	№7
№ испы­туемых п/п	Время решения первого задания теста в сек.	Ранги времени решения первого задания теста	Время решения второго задания теста в сек.	Ранги времени решения второго задания теста	Время решения третьего задания теста в сек.	Ранги времени решения третьего задания теста
				2,5		2,5
Сумма рангов				15,5		10,5

2. Суммирование полученных рангов по столбцамтаблицы 6.8.

В столбце 3 получена сумма рангов равная 10, в столбце 5 -равная 15,5 и в столбце 7 — равная 10,5.

3. Подсчет общей суммы рангов: 10 + 15,5 + 10,5 = 36.

4. Подсчет суммы рангов по формуле (1.3):

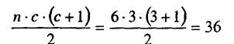
где с — число столбцов;

п — число строк или число испытуемых (что в данном случае одно и то же).

5. Проверка правильности ранжирования. Поскольку значения сумм рангов, полученных двумя разными способами совпали, следовательно, ранжирование проведено правильно.

6. Расчет эмпирического значения критерия Фридмана, осуществляемый по следующей формуле:

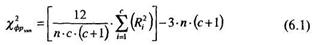
где п — количество испытуемых или строчек с — количество столбцов R_i. — сумма рангов i-того столбца

7. Подставляем в формулу 6.1 необходимые значения из таблицы 6.8, получаем

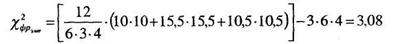
8. По таблице 3 Приложения определяем величины критических значений χ²_Фркр для числа испытуемых равному 6. Соответствующий блок таблицы 3. Приложения представлен в таблице 6.9:

Таблица 6.9

п	Р
0,052	0,012
	0,33	8,33

Подчеркнем, что с целью стандартизации предъявления табличных значений, критические значения, взятые из таблицы 3 Приложения даны в виде, соответствующем ранее использованному варианту. Следует особо подчеркнуть, что таблицы для поиска критических значений критерия Фридмана очень специфичны и отличаются от стандартных статических таблиц. Здесь уровни значимости Р — даны нетрадиционно, и поэтому каждый раз следует выбирать наиболее близкие значения к 0,05 и 0,01. В нашем случае эти значения составляют 0,052 и 0,012.

Переводя табличные значения в привычную форму записи, получаем:

Соответствующая «ось значимости» имеет вид:

Таким образом, полученное эмпирическое значение критерия Фридмана попало в зону незначимости. Отсюда следует, что статистически значимых различий во времени решения первых трех заданий теста нет.

Переформулируем полученный результат в терминах нулевой и альтернативной гипотез: поскольку между показателями, измеренными в трех разных условиях, существуют лишь случайные различия, то принимается нулевая гипотеза Н_о, т.е. гипотеза о сходстве, а гипотеза Н₁ отклоняется.

Еще одна специфическая особенность критерия Фридмана заключается в том, что в зависимости от числа измерений (условий), используются разные таблицы критических значений. На это следует особо обратить внимание, чтобы не допустить ошибочных статистических выводов.

Правила использования таблиц для нахождения критических значений в критерии Фридмана приведены ниже:

1. При общем количестве измерений равном 3 и числе испытуемых от 2 до 9 критические значения критерия Фридмана определяются по таблице 3 Приложения.

2. При общем количестве измерений равном 4 и числе испытуемых от 2 до 4 критические значения критерия Фридмана определяются по таблице 4 Приложения.

3. При большем количестве измерений и испытуемых критические значения критерия Фридмана определяются по таблице 12

Приложения для критерия хи-квадрат. В этом случае число степеней свободы определяется по формуле v = с - 1, где с — количество условий измерения. (Подробнее о критерии хи-квадрат см. ниже глава 8).

С целью более глубокого овладения критерием Фридмана рассмотрим еще один вариант задачи, но уже для первых четырех заданий теста.

Задача 6.5.Анализируя результаты предшествующей работы с критерием Фридмана психолог предположил, что время решения четвертого задания будет значимо отличаться от времени решения первых трех заданий.

Решение. Результаты всех четырех измерений приведены в таблице 6.10, в которой произведено ранжирование всех измерений по строкам и суммирование рангов по столбцам.

Таблица 6.10

№ 1	№ 2	№ 3	№ 4	№ 5	N9 6	№ 7	№ 8	№ 9
№ испы- туе- мых п/п	Время реше- ния пер- вого зада- ния теста в сек.	Ранги вре- мени реше- ния первого зада- ния теста	Время реше- ния второ- го за- дания теста веек.	Ранги вре- мени реше- ния второ- го за- дания теста	Время реше- ния тре- тьего зада- ния теста в сек.	Ранги вре- мени реше- ния третьего зада- ния теста	Время реше- ния чет- вертого зада- ния теста в сек.	Ранги времени реше- ния чет- верто- го за- дания теста
				2,5		2,5
Сумма рангов				19,5		11,5

Опускаем объяснения ряда операций, которые даны выше и проверим только правильность ранжирования. Как следует из таблицы 6.10 общая сумма рангов составила: 11 + 19,5 + 11,5 + 18 = 60. Согласно расчетной формуле (1.3):

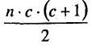она должна быть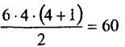

Равенство полученных сумм подтвердило правильность ранжирования. Определяем эмпирическое значение критерия по формуле (6.1):

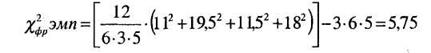
Поскольку в данном примере рассматривается четыре измерения, а количество испытуемых больше 4, то критические величины находятся по таблице 12 Приложения для критерия хи-квадрат. Число степеней свободы определяется по формуле v = с - 1 или v = 4 - 1 = 3. Используя привычную форму записи для критических величин, получаем следующее выражение:

«Ось значимости» в этом случае имеет вид:

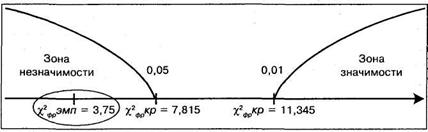
И вновь полученное эмпирическое значение критерия Фридмана попало в зону незначимости. Следовательно второе предположение психолога не подтвердилось, или, иначе, в терминах статистических гипотез — вновь принимается гипотеза H_о о сходстве времени решения первых четырех заданий теста.

Для применения критерия Фридмана необходимо выполнять следующие условия:

1. Измерение должно быть проведено в шкале интервалов или отношений.

2. Выборка должна быть связной.

3. В выборке должно быть не менее двух испытуемых, каждый из которых имеет не менее трех измеренных показателей. Верхний предел для количества испытуемых не определен, а количество измерений не может превышать 100 (см. таблицу 12 Приложения).

4. В зависимости от числа измерений и количества испытуемых используются разные таблицы значимости (правила выбора таблиц см. выше).

Критерий Пейджа

Критерий Пейджа (его полное название L критерий тенденций Пейджа) можно рассматривать как эквивалент критерия Фридмана для сопоставления показателей измеренных в трех и более условиях на одной и той же выборке испытуемых. Однако этот критерий не только позволяет выявить различия, но указывает на направление в изменении величин признака. Именно поэтому он является более предпочтительным.

Так, например, критерий Пейджа позволяет проверить предположения о временной или ситуативно обусловленной динамике изменения каких-либо признаков. К сожалению, применение этого достаточно мощного критерия ограничено объемом выборки — число испытуемых не может быть больше 12 и числом измерений признака — оно не может быть больше 6.

Задача 6.6.Решим еще раз задачу 6.5, но уже помощью критерия Пейджа, используя уже готовую таблицу 6.10. При этом основной тенденцией данного примера будем считать увеличение времени решения второго и четвертого заданий по сравнению с первым и третьим заданиями.

Решение. Подчеркнем, что первые несколько операций аналогичны операциям критерия Фридмана. Поэтому их описание мы опускаем и отсылаем к предыдущему критерию.

Дальнейшая работа с критерием Пейджа заключается в преобразовании таблицы 6.10. Следует попарно переставить столбцы таблицы 6.10, ориентируясь на величины сумм рангов так, чтобы в начале таблицы стояли столбцы с наименьшей суммой рангов, а в конце таблицы — с наибольшей. Понятно, что столбцы с соответствующими измерениями также переставляются. После проведения необходимых перестановок получается таблица 6.11.

Таблица 6.11

№ 1	№ 2	№3	№4	№ 5	№6	№7	№ 8	№ 9
№ испы- туе- мых п/п	Время реше- ния первого задания теста в сек	Ранги вре- мени реше- ния первого задания теста	Время решения третьего задания теста в сек.	Ранги времени решения третьего задания теста	Время решения четверто- го задания теста в сек.	Ранги времени решения четверто- го задания теста	Время решения второго задания теста в сек.	Ранги времени решения второго задания теста
				2,5				2,5
Сумма рангов				11,5				19,5

Теперь все готово для подсчета эмпирического значения L_эмп критерия Пейджа. Оно определяется по формуле:

где R_i. — сумма рангов i -того столбца в упорядоченной таблице

i— порядковый номер столбца, получившийся в новой таблице, упорядоченной по сумме рангов.

с — число измерений.

Используя формулу (6.2) вычисляем эмпирическое значение L_эмп для нашего примера:

L_эмп = (11 • 1) + (11,5 • 2) + (18 • 3) + (19,5 ∙ 4) = 166

По таблице 5 Приложения определяем критические значения L_эмп для числа испытуемых п = 6 и для числа измерений с = 4. Отметим, что в таблице критических значений критерия Пейджа добавлен уровень значимости 0,001 или 0,1%. Представим соответствующий блок таблицы 5 Приложения в виде таблицы 6.12.

Таблица 6.12

№ — число испытуемых	С — количество измерений 4	Р — уровень значимости Р
		0,001
	0,01
	0,05

Используя привычную форму записи для критических величин, получаем следующее выражение:

Строим «ось значимости»:

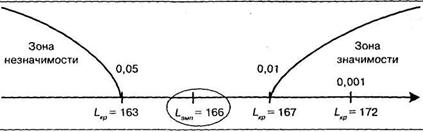
В нашем примере значение L_эмп попало в зону неопределенности, следовательно, можно считать, что тенденция увеличения времени решения заданий теста №№ 2 и 4 по сравнению с заданиями №№ 1 и 3 оказалась значимой на уровне 5%.

Переформулируем полученный результат в терминах нулевой и альтернативной гипотез: поскольку между показателями, измеренными при решении четырех заданий теста, существуют не случайные различия на 5% уровне значимости, то нулевая гипотеза Н_о, т.е. гипотеза о сходстве отвергается, и принимается альтернативная гипотеза Н₁ о наличии различий.

Сравнивая выводы, полученные при решении задачи 5 с помощью критериев Фридмана и Пейджа, можно подумать, что они не согласуются друг с другом. Однако это не совсем так. Эти критерии обращаются к разным сторонам анализируемого материала, характеризуя различные аспекты обрабатываемых данных. Если первый критерий — Фридмана — выявляет наличие различий в измеренных показателях (признаках), то критерий Пейджа позволяет выявить тенденцию в изменениях величин измеряемых признаков.

Приведем еще один пример использования критерия Пейджа.

Задача 6.7. Психолог высказывает предположение о наличии следующей тенденции: время решения заданий теста будет возрастать по мере увеличения их сложности.

Решение. Для выявления этой тенденции психолог сравнивает время решения пяти заданий теста у тех же шести испытуемых. Поскольку начальные операции с данными представлены выше, то результаты обработки по критерию Пейджа сразу представим в виде таблицы 6.13.

Как всегда необходимо проверить правильность ранжирования. Общая сумма рангов составила: 11 + 22 + 11,5 + 19 + 26,5 = 90

Согласно формуле (1.3): 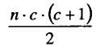она должна быть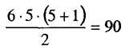

Таблица 6.13

№ испы- туе- мых п/п	Время реше- пер- вого зада- ния теста в сек.	Ранги вре­мени реше- ния пер- вого зада- ния теста	Время реше- ния второ- го за- дания теста в сек.	Ранги вре- мени реше- ния второ- го за- дания теста	Вреп.>. реше- ния тре- тьего зада- ния теста в сек.	Ранги вре­мени реше- ния тре- тьего зада- ния теста	Время реше­ния чет- верто- го зада- ния теста в сек.	Ранги вре­мени реше- ния чет- верто- го за- дания теста	Время реше- ния пято го за- дания в сек.	Ранги вре- мени реше- ния пятого зада- ния теста
				2,5		2,5
				4,5						4,5
Сумма рангов						11,5				26,5

Сравнив результаты первого и второго подсчета рангов, делаем вывод о том, что ранжирование произведено правильно.

Теперь, чтобы подсчитать L_эмп по формуле (6.2), не будем строить новую таблицу, а применим второй способ вычислений. Для этого рассмотрим сумму рангов как обычный ряд чисел и проранжируем этот ряд. Причем каждой величине этого нового, упорядоченного ряда поставим в соответствие его ранг. Этот ранг в формуле (6.2) обозначен как индекс L. Поэтому получатся следующие соответствия:

11→ i = 1; 11,5 → i = 2; 19→ i = 3; 22→= 4; 26,5 →i = 5

Теперь, имея суммы рангов и соответствующие им индексы, можно применить формулу (6.2):

L_змп = (11 • 1) + (11,5 • 2) + (19 • 3) + (22 • 4) + (26,5•5) = 311,5

Следующим этапом, как всегда, является нахождение критических величин для соответствующего числа испытуемых и измерений.

По таблице 5 Приложения находим для п = 6 и с = 5:

Строим соответственно «ось значимости»:

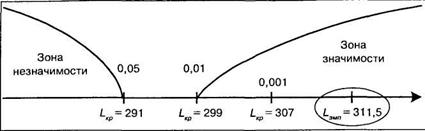
Полученная величина L_эмп критерия тенденций Пейджа оказалась значимой на 0,1% уровне. Следовательно, по мере увеличения сложности заданий, увеличивается и время их решения.

В терминах статистических гипотез полученный результат таков: Н_о — нулевая гипотеза о сходстве должна быть отвергнута, а на уровне 0,1% следует принять альтернативную гипотезу Н₁ о наличии различий. Иными словами, тенденция увеличения времени решения заданий теста с увеличением их сложности не является случайной.

Для применения критерия Пейджа необходимо соблюдать следующие условия:

1. Измерение может быть проведено в ранговой, интервальной и в шкале отношений.

2. Выборка должна быть связной.

3. В выборке должно быть не менее двух и не больше 12 испытуемых, каждый из которых имеет не менее трех измеренных показателей.

4. Применение критерия ограничено, так как таблицы критических значений рассчитаны на небольшую выборку (n ≤ 12) и маленькое число измерений (не больше 6). Если эти ограничения не выполняются, приходится использовать критерий Фридмана.

Критерий Макнамары

Критерий Макнамары очень прост, однако его использование имеет некоторые особенности и требует определенных навыков в статистических расчетах и работе с таблицами критических величин. Этот критерий относится также к числу непараметрических критериев и предназначен для работы с данными, полученными в самой простой из номинальных — в дихотомической шкале. Рассмотрим примеры его использования.

Задача 6.8. Психолога интересует вопрос — является ли выбранный им способ профессиональной ориентации к профессии экономиста достаточно эффективным?

Решение. Для решения этой задачи школьный психолог проводит эксперимент по выявлению эффективных форм профориентационной работы к профессии экономиста среди учащихся выпускных классов. С этой целью он использует такие мероприятия, как беседы, экскурсии, циклы лекций и т.п. Отношение 20 учащихся к этой профессии выяснялось до и после проведения профориентационной работы.

Школьники отвечают на вопросы о профессии экономиста по следующему правилу: нравится (кодируется цифрой 1), не нравится — (кодируется цифрой 0). Таким образом, экспериментальные данные получены психологом в самой простой шкале — дихотомической. Результаты двукратного опроса 20 учащихся записаны в форме таблицы 6.14 имеющий формат 2×2. Таблицы подобного рода называют также четерехпольными таблицами. Поля в этих таблицах обозначаются заглавными латинскими буквами А, В, С и D. Иногда используют маленькие буквы a, b, с и d.

Таблица 6.14

		Второй опрос	Сумма
Нравится	Не нравится
Первый опрос	Нравится	А = 2	В = 2
Не нравится	С = 11	D = 5
	Сумма

В Таблице 6.14 «А» — обозначает число учащихся, которые и до и после профориентационной работы дали ответ «нравится, «С» — число учащихся, которые первый раз дали ответ «не нравится», а второй раз «нравится», «B» — число учащихся, ответивших первый раз «нравится», а второй раз «не нравится», «D» — число учащихся, оба раза ответивших «не нравится».

Подчеркнем, что возможна ситуация, в которой В = С. В этом случае критерий Макнамары не может быть применен. Следует воспользоваться критерием хи-квадрат.

Напомним, что психолога интересует вопрос — является ли эффективной выбранная им система ориентации учащихся к профессии экономиста?

Работа по критерию Макнамары начинается с выяснения вопроса о том, будет ли сумма чисел, стоящих в ячейках В и С, меньше или равна 20 или эта сумма будет превышать число 20.

В первом случае, т.е. когда сумма чисел В + С≤20 используется один способ расчета по критерию. Назовем его — способ А. Если сумма чисел, стоящих в ячейках В + С > 20 — используется другой способ. Назовем его способ — Б.

Способ А.Пусть сумма (В + С) < 20 тогда дальнейший расчет по критерию Макнамары производится следующим образом:

1. Находится наименьшая величина из величин В я С, которая обозначается буквой т, т.е т = min (В, С).

2. Находится сумма величина В + С, которая обозначается буквой п, т.е. п = В + С.

3. По таблице 6 Приложения на пересечении строк таблицы т и п находится величина М_эмп. Особо подчеркнем, что, в отличие от всех критериев, по таблице 6 Приложения находятся не критические величины, а именно эмпирическое значение критерия Макнамары. Это принципиальное отличие этого критерия от всех других.

4. Величины М_к в случае способа А являются постоянными и равны соответственно 0,025 для 5% уровня и 0,005 для 1% уровня значимости.

5. Строится соответствующая «ось значимости».

6.На «ось значимости» наносится М_эмп, найденное по таблице 6 Приложения.

7.Осуществляется статистический вывод по критерию Макнамары.

Способ Б.Пусть сумма (В +С) > 20.

1. Производится расчет М_эмп по следующей формуле:

М_эмп=(B-C)²/(B+C) (6.3)

2. Находятся критические величины М_к по таблице 12 Приложения для критерия хи-квадрат с числом степеней свободы v = 1 (см. глава 8, п. 8.1.). Однако поскольку величина степени свободы критерия хи-квадрат в данном случае всегда постоянна и равна 1, то критические величины М_кр так же, как и в случае способа А, всегда одни и те же и равны М_кр = 3,841 для 5% уровня значимости и М_кр = 6,635 для 1% уровня значимости. В традиционной форме записи это выглядит так:

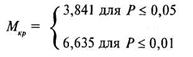
3. Строится соответствующая «ось значимости».

4.На «ось значимости» наносится М_эмп,,подсчитанное по формуле (6.3).

5.Осуществляется статистический вывод по критерию Макнамары.

Продолжим решение нашей задачи.

В ней п = (В + С) = 2 +11 = 13 < 20 — следовательно необходимо применить первый способ. В нашем случае т = 2 — как наименьшая из величин В и С.

Поэтому, чтобы получить М_змп (подчеркнем еще раз, а не М_кр — как обычно!) — следует обратиться к таблице 6 Приложения. В ней находим в левом крайнем столбце величину п = 13. Это число есть сумма В + С = 13.

В верхней строчке находим число т = 2 — это минимальное из чисел В и С. На пересечении соответствующей строчки и столбца стоит число 011.

Нужная нам ячейка таблицы 6 Приложения вынесена в таблицу 6.15:

Таблица 6.15

п /т

Примечание. Нули в таблице 6 Приложения опущены, поэтому к любому числу, найденному по этой таблице, нужно слева добавить нуль и запятую, так чтобы получить необходимую величину в виде: 0, (число, взятое из таблицы) Таким образом, из таблицы 6 Приложения и таблицы 6.15 следует, что М_эмп = 0,011.

Можно еще раз, хотя это и не обязательно в данном конкретном случае, воспользоваться традиционной формой записи:

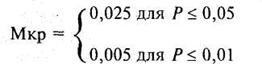
Следует построить «ось значимости»:

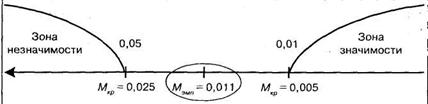
Поскольку М_эмп попало в зону неопределенности, то на 5% уровне значимости можно отклонить гипотезу Н_о о сходстве и принять альтернативную гипотезу Н₁ о различии, иными словами на 5% уровне значимости можно сделать вывод о том, что разработанный и примененный психологом цикл лекций, бесед и экскурсий способствовал формированию у школьников положительного отношения к профессии экономиста.

Продолжим знакомство с критерием Макнамары. Для этого решим следующую задачу:

Задача 6.9.Психолог выясняет вопрос — будут ли обнаружены различия в успешности решения двух, различных по сложности, мыслительных задач? Для решения этого вопроса группа из 120 учащихся решала оба типа задач.

Решение. Полученные результаты сразу представим в виде таблицы 6.16:

Таблица 6.16

		Первая	Задача	Сумма
Решена верно	Решена неверно
Вторая задача	Решена верно	А = 50	В = 31
Решена неверно	С= 19	D = 20
	Сумма

Из таблицы 6.16 следует, что 50 учащихся верно решили обе задачи, 19 верно решили первую задачу и неверно вторую, 31 — неверно решили первую задачу и верно вторую, 20 — неверно решили обе задачи.

Прежде всего, вычислим сумму (В+С) = 31 + 19 = 50. Она оказалась больше 20, следовательно, необходимо применить способ Б работы с критерием Макнамары и вычисление М_эмп следует проводить по формуле (6.3):

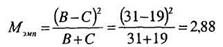
Мы помним, что при п > 20 величины М_кр равны 3,841 для 5% уровня значимости и 6,635 для 1% уровня значимости. Следовательно, в традиционной форме записи

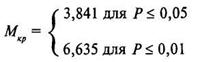
П