Дифференцирование обратных функций

Перейдем к рассмотрению производной обратной функции.

Пусть дифференцируемая и строго монотонная функция на некотором промежутке X. Если переменную y рассматривать как аргумент, а переменную x как функцию, то новая функция является обратной к данной и, как можно показать, непрерывной на соответствующем промежутке Y.

Теорема 3.5.Пусть функция 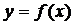является непрерывной и строго монотонной в некоторой окрестности точки и имеет в этой точке производную Тогда обратная функция также имеет в соответствующей точке производную, причем

(3.5)

Доказательство.По условию функция дифференцируема и

Пусть приращение независимой переменной y, соответствующее приращение обратной функции Тогда справедливо равенство

(3.6)

Переходя к пределу в равенстве (3.6) при и учитывая, что в силу непрерывности обратной функции получим

т.е.

Формула (3.5) имеет простой геометрический смысл. Если 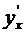выражает тангенс угла наклона касательной к кривой к оси 0x, то тангенс угла наклона той же касательной к оси 0y, причем (если и - острые углы) (рис. 3.9) или (если и - тупые углы). Для таких углов или Этому равенству и равносильно условие

Рис. 3.9

Пример. . Обратная функция . Тогда ( рассматриваем на отрезке , где , поэтому перед корнем выбран знак «+»).

Таблица производных

На практике чаще всего приходится находить производные от сложных функций, поэтому аргумент 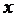заменим на промежуточный аргумент « ».

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

Пример. Найти производную функции

Решение. Данную функцию перепишем в виде:

Тогда

Производная от функции, заданной параметрически

Пусть 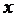и заданы как функции некоторого параметра : , . Предположим, что функции и имеют производные по переменной в рассматриваемой области изменения этой переменной и . Кроме того, предположим, что функция в окрестности рассматриваемой точки имеет обратную функцию . Найдем производную . По правилу дифференцирования обратной функции . Функцию 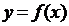, определяемую параметрическими уравнениями , можно рассматривать как сложную функцию , где . По правилу дифференцирования сложной функции: . Тогда: , т.е.

(3.7)

Эта формула позволяет находить производную от функции, заданной параметрически, не находя непосредственной зависимости y от .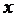

Пример

Пусть . Найти .

Решение

; , тогда

Пример

Пусть . Найти

Решение

Тогда

Логарифмическая производная

В ряде случаев для нахождения производной целесообразно заданную функцию сначала прологарифмировать, а затем продифференцировать результат. Такую операцию называют логарифмическим дифференцированием.

Пусть функция 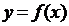положительна и дифференцируема в данной точке 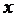. Тогда в этой точке существует . Рассматривая как сложную функцию аргумента 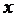, мы можем вычислить производную этой функции в данной точке 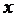, принимая 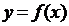за промежуточный аргумент. Получаем:

.

Эта величина называется логарифмической производной функции 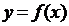в данной точке .

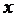Вычислим логарифмическую производную степенно-показательной функции . Допустим, что , - непрерывные и дифференцируемые функции; . Тогда , . Учитывая, что , получаем: .

Примеры

1) Пусть . Найти .

Решение.Прологарифмируем данное выражение

Найдем производную от левой и правой части, считая y зависящей от x.

Выразим

2) Пусть . Найти .

При нахождении производной от дроби получим громоздкое выражение, поэтому сначала прологарифмируем функцию.

;

Найдем производную от левой и правой части этого уравнения, считая y зависящей от x.

Выразим ;

.

3.12. Производная неявной функции

Рассмотрим дифференцирование неявной функции, заданной уравнением

Для нахождения производной функции y, заданной неявно, нужно продифференцировать обе части уравнения, рассматривая y как функцию от x, а затем из полученного соотношения найти производную

Пример. Найти производную функции y, заданную уравнением

Решение. Дифференцируя обе части равенства и учитывая, что y есть функция от x, получим

откуда

Замечание.В дальнейших разделах данного пособия нам потребуется понятие производной функции многих переменных. Частная производная функции по аргументу является обыкновенной производной функции одной переменной при фиксированных значениях других переменных (то есть считаем аргументом, все остальные - константами ). Обозначается такая производная

Теория функции нескольких переменных выходит за рамки данного пособия (см. часть 3).

Дифференциал функции

Пусть функция 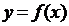дифференцируема в точке Тогда по определению (3.2) дифференцируемости функции ее приращение в этой точке может быть представлено в виде

(3.4)

где A – некоторое число, не зависящее от приращения 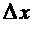, а бесконечно малая функция при Если то при 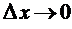величина является бесконечно малой одного порядка с 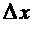, а бесконечно малая более высокого порядка малости по сравнению с .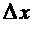

Тогда будет главной частью приращения , обусловленного приращением аргумента .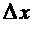

Определение 3.4. Дифференциалом функции 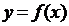в точке соответствующим приращению 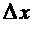аргумента x, называют главную линейную относительность 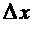часть приращения функции в этой точке

Но по теореме 3.1 имеем и можно записать:

Найдем дифференциал независимой переменной. Пусть

Тогда:

Учитывая, что , получаем:

т.е. дифференциал независимой переменной равен её приращению и справедлива запись:

(3.8)

Из равенства (3.8) производную в любой точке x можно вычислить как отношение дифференциала функции dy к дифференциалу независимой переменной dx:

, тогда имеем: (3.9).

Поскольку дифференциал dy функции 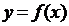отличается от производной лишь независящим от x сомножителем dx, то для вычисления дифференциалов можно использовать правила дифференцирования и формулы производных элементарных функций. Например:

1)

2)

3)

4)

5)

Так, для дифференциала произведения дифференцируемых функций и