Фильтрация мощных помех и квазиоптимальный приемник

ШПС

Для борьбы с мощными помехами в системах связи применяют широкополосные (шумоподобные) или сложные сигналы с приемом СФ или коррелятором. При этом ОСП на выходе СФ равно

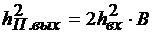, (4.7)

где ОСП 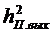, (1.3) и ОСП в (4.7), определяющее помехоустойчивость приема, связаны соотношением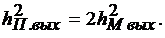

Увеличением базы В можно подавить любую помеху с ограниченной мощностью. Актуальность такого подавления следует из теоремы Шеннона о пропускной способности канала связи с шумами 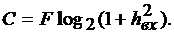При мощной помехе 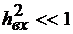→ 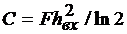откуда

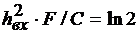(4.8)

Если в (4.7) заменить Т на 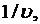то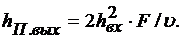

Сравнивая это равенство с (4.8), можно отметить, что если 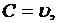т.е. вести передачу информации со скоростью С, то значение 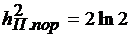является пороговым.

Таким образом, согласно теореме можно вести передачу информации по такому каналу со сколь угодно малой вероятностью ошибки, если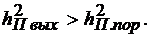

Помехи с ограниченной мощностью разделяются по частотно-временным свойствам на сосредоточенные, узкополосные, импульсные и структурные, которые представлены на рис.4.2, где штриховкой выделены ЧВЭ, пораженные структурной помехой в виде ДЧ сигнала, а толстой линией выделены узкополосные (F_y) по спектру и сосредоточенные по времени импульсные (T_u) помехи.

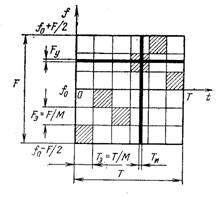
Рис.4.2. Частотно-временные помехи с ограниченной мощностью.

Cосредоточенными помехами называют такие, у которых ширина спектра F_п=F, т.е. совпадает с шириной спектра всего сигнала. Для узкополосной помехи F_y<< F, а импульсной T_u<<T.

В [1] показано, что помехоустойчивость приема ШПС при воздействии комплекса помех с ограниченной мощностью или спектральной плотностью мощности определяется ОСП (4.7) на выходе СФ. Для повышения помехоустойчивости необходимо применять

М -ичные алфавиты. Будем рассматривать четыре, наиболее распространенные, типа ШПС рис.4.3:

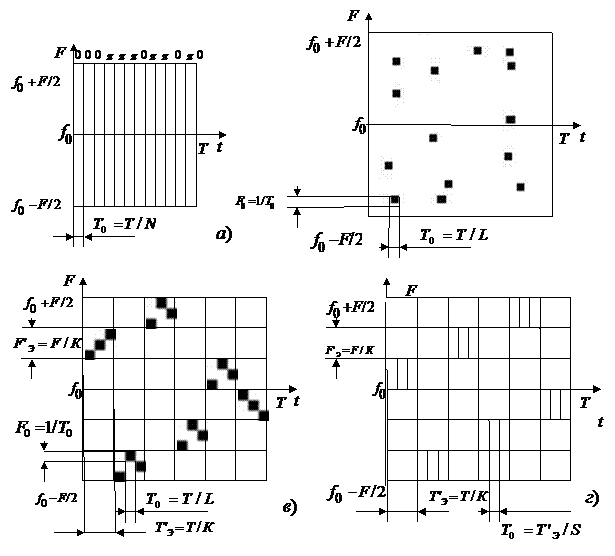
Рис.4.3. Виды ШПС: а) ФМ сигнал; б) ДЧ сигнал;

в) ДСЧ-ЧМ сигнал; г) ДСЧ-ФМ сигнал

а) ФМ сигнал из N радиоимпульсов длительностью T₀=T/N;

б) ДЧ сигнал из L радиоимпульсов, каждый из которых расположен на прямоугольнике со сторонами T₀ и F₀;

в) ДСЧ-ЧМ, состоящий из L радиоимпульсов, которые сгруппиро-ваны в К ЧВЭ длительностью T'_э и шириной спектра F_э';

г) ДСЧ-ФМ, состоящий из К ЧВЭ длительностью T'_э и шириной спектра F_э', каждый которых содержит S ФМ радиоимпульсов с энергией радиоимпульса в вертикальной полосе со сторонами T₀ и F_э'.

Как показано в [3] при стационарной сосредоточенной помехе с неравномерным спектром коэффициент передачи «обеляющего» СФ определяется выражением Котельникова:

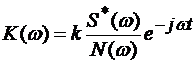(4.9)

где 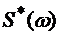- сопряженный по Гильберту амплитудный спектр сигнала, а

N^-1(ω) – «обеляющий» фильтр; k- соnst.

Согласно этому выражению K(ω) является переменным по частоте в зависимости от неравномерности спектра помех.

Адаптивный приемник ШПС.

При адаптивном приеме ШПС будем анализировать совместное распределение помехи и сигнала на частотно-временной плоскости (рис.4.2, рис.4.3). Согласно этому распределению будем изменять коэффициент передачи «обеляющего» СФ в соответствии с (4.9).

Реализация адаптивного приемника ШПС на основе «обеляющего» СФ с непрерывным переменным коэффициентом передачи наиболее проста при аппроксимации K(ω) в М частотных интервалах дискретной функцией, т.е. в случае реализации его в виде М -канального СФ. В каждом из этих каналов все частотно-зависимые элементы остаются постоянными, а изменяется только коэффициенты усиления каналов 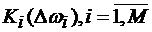. Схема такого адаптивного приемника приведена на рис.4.4.

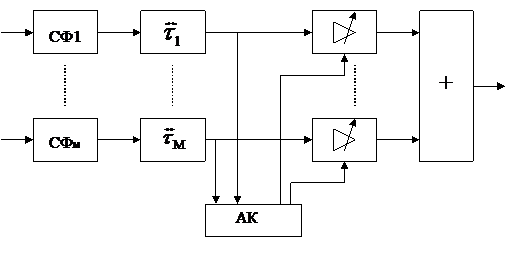
Рисунок 4.4. Адаптивный многоканальный приемник ШПС.

Каждый из М каналов содержит элементарный СФ_i для ЧВЭ сигнала (рис.4.3), линию задержки (ЛЗ), которая компенсирует время задержки τ_i ЧВЭ относительно окончания ШПС (t=T), когда пики АКФ ЧВЭ совпадают и осуществляется когерентное накопление ЧВЭ.

Анализатор каналов (АК) в момент t=T производит анализ отсчетов напряжений на выходах СФ_i и определяет с учетом оценок уровней помех и сигналов значения 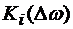, т.е. веса, с которыми напряжения на выходах СФ_i входят в общую сумму.

Помехоустойчивость такого приемника при действии помех, энергия которых каким-то образом сосредоточена в отдельных ЧВЭ базисного прямоугольника (рис.4.2), зависит от числа совпадений ЧВЭ сигнала и помехи, а также зависит от ОСП на выходе СФ_i (элементарного ОСП).

В [1] показано, что рассматриваемые ШПС рис.4.3 обладают одинаковыми характеристиками с точки зрения числа совпадений ЧВЭ сигнала и помехи различного вида, причем относительное число совпадений равно 1/М. Однако, ШПС ДСЧ-ЧМ и ДСЧ-ФМ позволяют иметь меньшее число каналов в адаптивном приемнике, если СФ_i являются СФ с ЧМ или ФМ ЧВЭ. Поэтому далее будем рассматривать адаптивный приемник для ДСЧ-ЧМ и ДСЧ-ФМ ШПС, а полученные результаты будут справедливы и для других ШПС, т. к. эти результаты зависят от относительного числа «пораженных» ЧВЭ.

Отметим, что метод, основанный на определении числа «пораженных» ЧВЭ и элементарных ОСП, применим для помех, не коррелированных с ШПС.

Будем полагать также, что при приеме ЧВЭ ШПС в отдельных каналах не коррелированы, а когерентное накопление ЧВЭ эквивалентно разнесенному приему ЧВЭ каналов с соответствующим сложением независимых по замираниям ветвей разнесения [14].

Линейное накопление (сложение) ЧВЭ.

Пусть поражены помехой мощностью 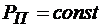т из М ЧВЭ, а в (М-т) каналах действует только АБГШ со СПМ N₀, для которых элементарное ОСШ на выходе элементарного СФ равно:

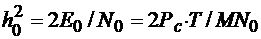(4.10)

Для этого случая выходное ОСП на выходе линейного (т.е. без учета знаменателя в (4.9)) накопителя ЧВЭ (т.е. фильтра, согласованного только при АБГШ) равно [1]:

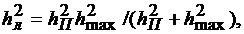(4.11)

где

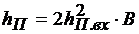- - ОСП на выходе СФ, когда шума нет и поражаются все М элементов; В=FТ=В₀M²; В₀=F_эТ_э; 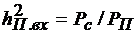- ОСП на входе СФ;

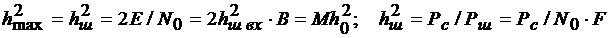- -ОСШ на выходе СФ при АБГШ, которое с учетом (4.10) равно .

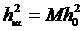На рис.4.5 представлена (прямая 1) относительная зависимость 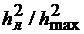от т/М, построенная в соответствии с (4.11).

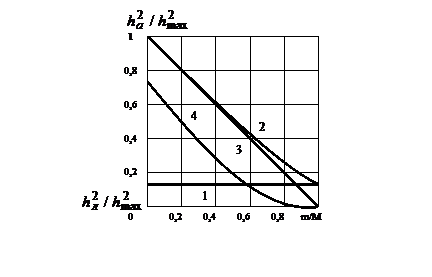
Рис.4.5. Графики относительного ОСП на выходе приемника ШПС

в зависимости от числа m пораженных помехой каналов: 1- СФ без БЗ

от помех (линейное сложение); 2,3 - СФ с БЗ от помех (адаптивный

приемник); 4 –нелинейный СФ с БЗ в виде идеального ограничителя.

Так как (4.11) не зависит от т, то прямая 1 параллельна оси абсцисс. При этом отношение 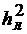на выходе СФ (4.11) всегда меньше наименьшего из отношени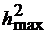й: или 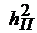, что еще раз подтверждает неэффективность линейного сложения при разнесенном приеме и сосредоточенных помехах с неравномерной СПМ.

Оптимальное накопление (сложение) ЧВЭ («обеляющий» СФ с блоком защиты (БЗ) от помех).

В адаптивном «обеляющем» СФ (4.9) напряжения с выходов элементных СФ суммируются в когерентном накопителе с весом по Бреннану [14]:

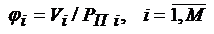, (4.12)

где 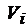- уровень огибающих сигнала в 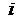-ом канале, а 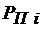- мощность помехи соответственно.

В этом случае ОСП на выходе адаптивного когерентного накопителя равно

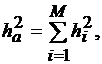(4.13)

где 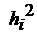- ОСП на выходе элементного СФ 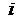- го канала.

Если положить, что в m каналах элементное ОСП (на выходе 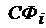) при действии помехи и шума равно 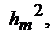а в остальных (М-т) элементах - 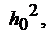то

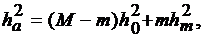
которое с учетом принятых обозначений может быть приведено к виду [1]:

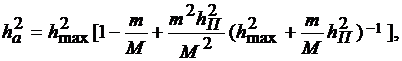(4.14)

Кривая 2 (рис.4.5) соответствует отношению 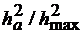и построена согласно (4.14).

При т<<М значение 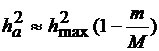и практически равно 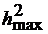(прямая 3), т.е. при т<<М влиянием ЧВЭ, пораженных мощной

помехой, в общем отношении сигнал/помеха можно пренебречь.

СФ с нелинейным БЗ от помех в виде идеального ограничителя.

Адаптивный приемник с нелинейным фильтром отличается от приемника рис.4.4 тем, что в каждом канале сначала стоит полосовой фильтр, затем идеальный ограничитель, после которого стоит узкополосный элементный СФ и линия задержки.

Отношение сигнал/помеха на выходе такого приемника (с БЗ в виде нелинейного СФ) равно:

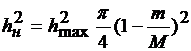. (4.15)

Зависимость 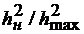от т/М представлена на рис.4.5 (кривая 4), которая меньше, чем в адаптивном приемнике (кривые 2,3). Это объясняется тем, что в нелинейном фильтре всегда остаются пораженные элементы, которые вносят в напряжение на выходе СФ помеху, равную по мощности ЧВЭ полезного сигнала, а при т/М >0,6 нелинейный фильтр уступает и СФ с линейным накоплением (т.е. СФ без БЗ).

Известно [1],что приемник ШПС, с рассмотренным выше нелинейным БЗ, является оптимальным фазовым обнаружителем, в котором ОСП на выходе при h²_вх<<1 надо уменьшать в π/4 раза (1дБ), а при h²_вх>>1 это отношение увеличивать в 2 раза (3дБ) согласно графику рис.4.6 изменения ОСП на выходе идеального ограничителя.

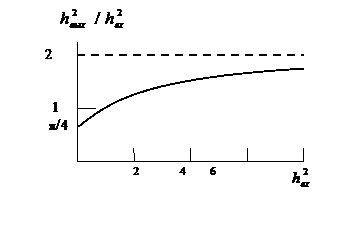
Рис.4.6. Изменение ОСП на выходе от ОСП

на входе идеального ограничителя.

Поэтому помехоустойчивость приемника ШПС с нелинейным БЗ можно оценить помехоустойчивостью оптимального приемника (например, ФМ сигналов) с указанным выше уменьшенным или увеличенным ОСШ, в зависимости от входного ОСП приемника.

Уместно отметить, что в радиоканалах, загруженных сосредоточенными по спектру мощными помехами, например, станционными помехами в КВ канале, адаптивный приемник ЧДС рис. 4.4 не обеспечивает требуемую надежность связи. В этом случае реализуют радиолинии ЧДС с адаптацией рабочей частоты (РЧ) и обратным каналом управления этой РЧ. По обратному каналу передается номер выбранной в качестве РЧ лучшей, например, по критерию ОСП частоты, из множества выделенных для связи частот. Вместе с тем выбор РЧ для ЧДС при заданном качестве связи является достаточно сложной задачей. Кроме того, например, при групповом использовании частот, актуальным является выбор в качестве РЧ максимального количества частот из множества выделенных для связи.

В статье [16] рассмотрены некоторые алгоритмы выбора РЧ для ЧДС с М=4, учитывающие структуру адаптивного приемника, и дана оценка вероятности выбора в качестве РЧ заданного количества частот из множества выделенных для связи.