Нелинейные последовательности

Для повышения помехозащищенности специальных перспективных систем связи применяют нелинейные ПСП, обладающие более высокой непредсказуемостью и объемом системы сигналов.

В качестве оценки непредсказуемости нелинейных ПСП принимают длину эквивалентного РСЛОС или эквивалентную степень∙k характеристического полинома (2.35) и называют её эквивалентной линейной степенью (ЭЛС) ПСП. Для М-последовательности ЭЛС равна∙k, а для нелинейных ПСП ЭЛС может достигать значения 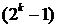, т.е. периода ПСП, что обеспечивает непредсказуемость нелинейных ПСП.

Алгоритм синтеза эквивалентного РСЛОС по известному принятому сегменту ПСП называют алгоритмом Берлекэлепа-Месси [7], ускоренный алгоритм реализации которого требует 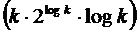операций.

Однако, в отличие от М – последовательностей сумма двух сдвинутых нелинейных последовательностей не является циклически сдвинутой относительно исходной нелинейной последовательности. Это свойство нелинейных последовательностей приводит к росту боковых пиков КФ по сравнению с М – последовательностями.

В настоящее время известны следующие нелинейные ПСП [5]:

1. Последовательности де Брейна, генерируемые РС с нелинейной обратной связью (рис.2.11 а).

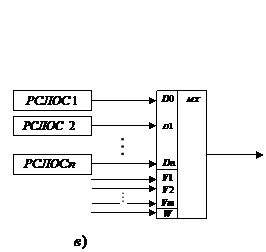
Рис.2.11. Схемы формирования нелинейных ПСП.

2. Последовательности, формируемые применением нелинейной внешней логики для комбинирования символов РСЛОС и имеющие период (длину) N = (2^k-1) (риc.2.11 б).

3. Составные нелинейные ПСП, формируемые чередованием символов с выходов двух и более РСЛОС по определенному правилу (рис.2.11 в).

а). Последовательности де Брейна имеют максимально возможный период N=2^k и большой ансамбль сигналов

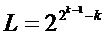(2.58)

и высокую непредсказуемость, определяемую ЭЛС:

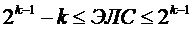, (2.59)

которая зависит от способа формирования ПСП.

При этом эти ПСП приближаются по статистическим свойствам к СП (нормальное распределение блоков в последовательности, сбалансированность «1» и «0» в периоде).

Наиболее простым является способ генерации последовательности де Брейна на основе РСЛОС формирования М-последовательности (рис.2.6). При этом в цепи обратной связи используется дополнительная нелинейная цепь в виде схемы совпадения «И», на входы которой поступают сигналы с инверсных выходов 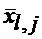l-ых триггеров РС, а выход подключен к входу триггера Т₁ (рис.2.12) через дополнительный сумматор.

T₁ T₂ T₃ T_k-1 T_k

x_0,j x_1,j x_2,j x_3,j x_k-1,j x_k,j

	X		X		X		X		X		X

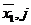
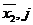
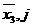
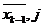
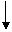C₁ C₂ C₃ C_k-2 C_k-1 С_k

Рис.2.12. Схема формирования нелинейной ПСП де Брейна.

Нелинейная ПСП содержит все возможные комбинации (полный код)

длительностью 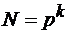, включая нулевую.

Прямой символ на входе l-го триггера на j+1 такте равен 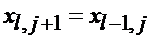и символ на входе первого триггера на j-м такте равен:

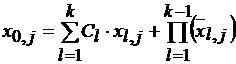, (2.60)

где .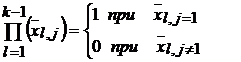

Используя очевидного равенство для выходов триггера 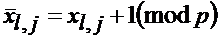можно из (2.60) получить аналогично (2.33) нелинейное рекуррентное уравнение формирования ПСП (для символа на входе Т₁ в j-м такте) в виде:

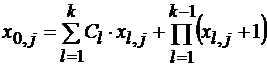. (2.61)

Хотя последовательность де Брейна, построенная данным способом, обладает ЭЛС=(2^k-1), многие авторы оспаривают эту цифру. Считают, что вся ПСП определяется также по 2k известным символам (не содержащим состояния из k нулей), т.к. она повторяет структуру М-последовательности. Общее число последовательностей ПСП для данного способа (сравни с (2.37)) равно:

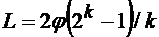(2.62)

Другие способы построения ПСП де Брейнаможно найти в [5].

Отметим, что нелинейные ПСП де Брейна целесообразно использовать в качестве синхронизирующих, например, в ШСС. Эти ПСП имеют хорошие периодические АКФ (ровное плато около главного пика R(0) и минимальное значение боковых пиков ).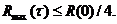

б). Последовательности, формируемые нелинейной внешней логикой. ЭЛС характеристического полинома ПСП является мерой сложности эквивалентного РС и определяется числом корней характеристического полинома. Увеличить их число можно внешним нелинейным комбинированием символов с выходов триггеров РСЛОС генератора М-последовательности.

К росту ЭЛС генерируемой нелинейной ПСП в наибольшей степени приводит операция умножения символов, выполняемая схемой «И», но

ухудшаются условие сбалансированности кода и КФ, а ЭЛС равно:

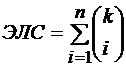, (2.63)

где 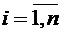- число операций умножения символов РСЛОС, производимых нелинейной внешней логикой; а k- число каскадов РСЛОС.

При n → k, ЭЛС→ к значению 2^k-1.

В [6] для формирования нелинейных ПСП с асимптотически оптимальными корреляционными свойствами предложена нелинейная функция комбинирования бент-функция (максимально нелинейная), имеющая равномерный спектр коэффициентов при разложении в дискретный ряд Уолша - Адамара. При этом функция комбинирования символов реализуется в след-ортогональном базисе, используя идентичное бент-функции след-ортогональное преобразование степенного базиса поля GF(2^k), формируемого РСЛОС. В результате выходные бент-последовательности могут быть синтезированы для четных 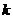и имеют период N=2^k-1, причем сбалансированы по числу «1» и «0» и имеют 3-х уровневые АКФ и ВКФ со значениями, не превышающими (2^k/2+1), что в 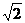раз меньше, чем у кодов Голда. Число нелинейных операций комбинирования определяет ЭЛС ПСП:

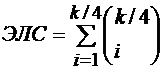. (2.64)

в). Составные нелинейные последовательности

Составными (комбинированными) называют последовательности, формируемые чередованием символов с выходов нескольких РСЛОС.

Простейший алгоритм формирования составной нелинейной ПСП –это перемножение символов с выходов двух РСЛОС, что соответствует перемножению элементов поля GF(2^k) первого РСЛОС на элементы поля GF(2^т) второго РСЛОС и получению элементов поля GF(2^kт).

При этом порядок ЭЛС = kт, а период составной нелинейной ПСП равен НОК ( N₁ =2^k -1, N₂ =2^m -1).

Однако, при этом нарушается условие сбалансированности кода (умножение ведет к росту числа «0») и, соответственно, ухудшаются корреляционные характеристики.

Для обеспечения сбалансированности кода составной ПСП известны разные способы «перемешивания» символов с выходов РСЛОС [6,8]. Например, Дженнингс предложил [5] алгоритм чередования символов с выходов РСЛОС, который формирует ансамбль составных ПСП, удовлетворяющих большинству вышеприведенных требований и реализуется схемой рис.2.13 на основе мультиплексора, управляемого регистром RG2.

RG1 и RG2: –два РСЛОС с n и m каскадами соответственно. Обозначим их через А и В соответственно.

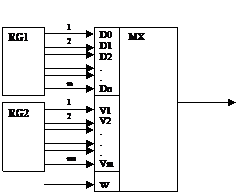
Рис.2.13. Схема формирования составной ПСП.

Алгоритм формирования нелинейной ПСП можно записать в следующем виде:

1.Выбирается целое k, 1≤ k ≤ m, такое что 2^k-1≤ п, причем если

2^m-1 ≤ п, то k = т.

2. Выбирается произвольно k каскадов задержки RG1 и, на каждый момент t_i, двоичное k состояние преобразуется в десятичное число:

,

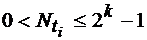причем если .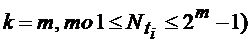

3. Выбирается отображение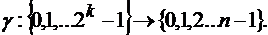

Порядок поступления символов RG1 на выход генератора ПСП

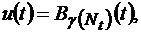
т.е. в качестве элемента чередования символов RG1 используется мультиплексор, управляемый RG2.

Период составной ПСП 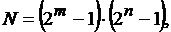при этом число единиц 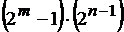и нулей 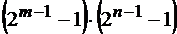в периоде, а ЭЛС при k = m равна

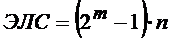. (2.65)

При этом среднеквадратическое значение уровня боковых пиков АКФ

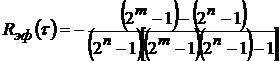. (2.66)

Если n >> m , то большинство боковых пиков АКФ

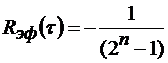(2.67)

Однако, отдельные боковые пики, расположенные на позициях,

кратных 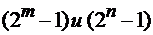могут превышать это значение.

Таким образом составные нелинейные ПСП обладают большой ЭЛС, хорошими характеристиками КФ и имеют более широкие возможности по генерации.

С другими алгоритмами генерации нелинейных ПСП, например, Касами – подобными нелинейными ПСП, студент может ознакомиться самостоятельно, используя литературу [6,7] и др. источники.

Псевдослучайные числовые последовательности

Следует отметить, что для защиты информации, например, в телекоммуникационных системах с кодовым разделением абонентов или компьютерных информационных сетях актуальными являются (в отличие от рассмотренных выше ШХС, получаемых оцифровкой уровней физического генерируемого случайного процесса) детерминированные вычислительные алгоритмы формирования ШХС в виде псевдослучайных числовых последовательностей.

Наиболее известными вычислительными алгоритмами являются [12] целочисленный конгруэнтный алгоритм Лемера и семейство алгоритмов Фибоначчи.

Алгоритм Лемера:

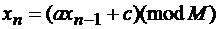(2.75)

где х₀ , а, с – заданные целые числа, (причем х₀ , а, с < M, а в качестве М взято некоторое большое число).

Алгоритмы Фибоначчи (алгоритмы с запаздыванием):

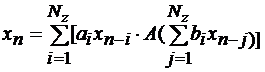(2.76)

где а_i, b_j равны нулю или 1; N_z - параметр запаздывания, 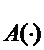- некоторый оператор, учитывающий фазовые соотношения между запаздывающими членами.

Случай 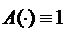соответствует обобщенному генератору Фибоначчи:

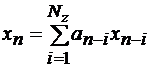, (2.77)

где параметр N_z - определяет число заданных (или вычисленных ранее) членов последовательности, которые надо хранить в памяти устройства, чтобы найти новый член ПСП на каждом следующим шаге алгоритма;

а_п-i - коэффициенты, которые обычно считают равными нулю или 1. Классический алгоритм Фибоначчи учитывает только два члена ряда: вычисленный на предыдущем шаге (п-1) и вычисленный на шаге (п- N_z).

Размерность фазового пространства (ФП) динамической системы определяется числом величин, которые надо задать, чтобы однозначно описать её состояние и иметь возможность найти состояние системы на следующем шаге вычисления. Очевидно, что размерность ФП динами-ческой системы, описываемой алгоритмом с запаздыванием, определяется параметром запаздывания N_z.

В силу ограниченности ФП алгоритма, заданного на конечном интер-вале [1, М] целых чисел, общее число всех состояний счетно и конечно. Поэтому, начиная с некоторого шага, результаты вычисления обязательно повторят ранее полученные значения, т.е. система выйдет на цикл, период которого зависит от начальных условий.

Для разработчика представляют интерес задачи исследования

зависимости этих циклов (периодов) и максимальных периодов ПСП,

определяющих помехозащищенность системы, от изменения интервала

[1, М] чисел, на котором задан алгоритм, и параметра запаздывания N_z , т.е. размерности ФП. Авторы [12] исследовали указанные выше задачи для алгоритма типа Фибоначчи формирования ПСП целых чисел {x_n} на заданном интервале [1, М] с параметром запаздывания N_z:

x_n= x_n-1 + x_n-Nz , (2.78)

где величина суммы x_n при вычислениях может быть меньше или равна 2М и выходит за верхнюю границу М области определения алгоритма. Поэтому этот алгоритм может быть дополнен оператором возвращения в указанный интервал [1, М], который реализует механизм перемешивания вычисленных чисел ПСП с определенным распределением вероятностей.

Авторами использован оператора возвращения - «сшивание» концов интервала, т.е. превышение разности (x_n–М) над величиной М прибавляется к величине нижней границы интервала, т.е. x_n= x_n – М.

Для вычисления значений ПСП, формируемой этим алгоритмом, необходимо задать параметры М , N_z и массив памяти (вектор запаз-дывания) 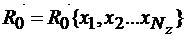, т.е. ряд начальных значений, состоящий из N_z целых чисел на интервале [1, М]. ФП такой системы имеет размерность 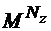и состоит из совокупности точек с координатами из интервала чисел [1, М], однозначно определяющих состояние системы.

Результаты исследования состояний динамической системы в ФП для данного алгоритма и более простого двумерного случая: N_z = 2 и М = 8 представлены на рис.2.16.

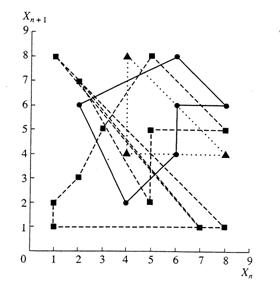
Рис.2.16. Последовательность состояний динамической системы в двумерном ФП для параметров алгоритма: М =8, N_z=2. Фазовые траектории циклов: с периодом Т(1)_8,2=3 (треугольники), Т(2)_8,2 = 6 (кружочки), Т(4)_8,2 = 12 (квадратики).

Эти результаты позволяют выявить следующие общие закономерности формируемых ПСП этим алгоритмом для случая больших размерностей N_z и значений М:

1. ФП алгоритма представляет набор циклов различного периода. Каждая точка состояния системы принадлежит только одному циклу, т.е. циклы не имеют общих точек.

2. Как правило, при заданных М и N_z, в ФП существует несколько различных циклов одинакового периода. Они отличаются совокупностью точек ФП. Число циклов с одинаковым периодом обозначим через ν: Т(ν)_М,Nz. Например, на рис.2.16 Т(2)_8,2 = 6 означает, что при М =8, N_z=2 в ФП существует два цикла с периодом равным 6.

3. При любых М и N_z точка, все координаты которой равны М, является изолированной, что следует из формулы (2.78) и операции возврата.

4. Точка с координатами (1,1,…1) при любых М и N_z всегда лежит на цикле с максимальным периодом. Точки (1,1,…1) и (М, М,…М) являются особенными во всем ФП.

5. Сумма точек состояний в ФП динамической системы по всем циклам всегда равна полному объему ФП: 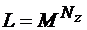. На рис.2.16 показаны три из 8 существующих фазовых траекторий (ФТ): Т(1)_8,2=3; Т(2)_8,2=6; Т(4)_8,2=12, а объем ФП равен 64, что совпадает с суммой точек по всем ФТ с учетом особой точки: (1+2+2×6+4×12=64).

Отметим, что ФТ при размерности ФП > 3 можно изучать только по их проекциям на соответствующие двумерные плоскости ФП рис.2.16.

Исследования также показали, что когда число М является не простым, а имеет сомножители, то ФТ ПСП воспроизводит ФТ сомножителей в большем масштабе и с тем же периодом. Кроме того, максимальный период ПСП растет при увеличении М, но не монотонно, т.к. не все простые числа М обеспечивают достижение максимального периода, т.е. простое число М не является для этого достаточным условием.

Следует отметить, что наличие в ФП большого числа циклов нежелательно, т.к. это приводит к уменьшению доли объёма ФП, который может быть занят циклами с максимальным периодом.