Особенности расчета надежности при постепенных отказах
Особенность расчетов при постепенных отказах состоит в учете информации о предшествующем состоянии объектов и возможности на базе этой информации строить экстраполяции на будущие времена. Поскольку надежность при постепенных отказах связана с изменением параметров элементов и системы в целом, часто для таких отказов употребляется термин параметрическая надежность. Параметрическая надежность, как указывалось выше, характеризует постепенный выход параметров (или одного, выбранного в качестве определяющего) из рабочей области 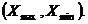 Устройство функционирует нормально, если его определяющие параметрынаходятся в определенных допустимых пределах
Устройство функционирует нормально, если его определяющие параметрынаходятся в определенных допустимых пределах 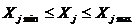 , т.е. если погрешности (отклонения) характеристик в реальных условиях эксплуатации не превосходят некоторой допустимой величины – допуска.
, т.е. если погрешности (отклонения) характеристик в реальных условиях эксплуатации не превосходят некоторой допустимой величины – допуска.
Значения показателей параметрической надежности существенно зависят от вида связей между элементами и вида характеристик изменения параметров, которые носят нестационарный, случайный характер. При этом полагают, что рабочая область изменения параметров устройства или системы не случайна и не меняется в течение работы системы.
Параметрической надежностью, в общем случае, называют вероятность Р того, что при работе в реальных условиях характеристики устройства не выходят за пределы поля допуска [3]:
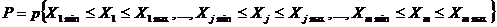 (16)
(16)
Задача анализа параметрической надежности устройства заключается в определении Р при известных законах распределения параметров хi или в расчете некоторых необходимых числовых характеристик вероятности Р при заданных числовых характеристиках функций распределения параметров.
Для фиксированного момента времени t вероятность нахождения системы в работоспособном состоянии, т.е. вероятность того, что определяющий параметр находится в заданных границах (Хmin, Хmax) определяется выражением:
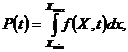 (17)
(17)
где f(Х,t) – плотность распределения значений параметра Х(t) в момент времени t.
Для вычисления параметрической надежности систем по данным измерений необходимо исследовать и экстраполировать изменения параметров элементов. Обычно исследуются лишь нестационарные монотонные составляющие процессов изменения параметров, связанные с регулированием, износом, старением.
В задачах прогнозирования технического состояния разрегулирования аппаратуры, износа механических конструкций используется веерное линейное изменение определяющих параметров:
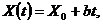 (18)
(18)
где X0 – фиксированное или случайное начальное значение параметра Х(t), b – случайная величина, распределенная по нормальному закону.
Для веерной модели Х(t) при рассчитанных параметрах α и β, чтобы найти время начала массовых отказов t = tH, необходимо решить уравнение [3]:
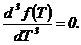 (19)
(19)
Это уравнение сводится к уравнению шестой степени. В результате его решения получается выражение, которое для практических целей можно аппроксимировать формулой:
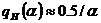 . (20)
. (20)
Наработка до начала массовых отказов определяется выражением:
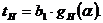 (4.21)
(4.21)
В настоящее время в связи с широким внедрением современных средств компьютерной математики наиболее перспективным аппаратом, позволяющим получить решение широкого класса задач надежности, является метод имитационного моделирования. В рамках этого метода представляется возможность исследования постепенных отказов путем вычисления частного значения определяющего параметра по частным реализациям параметров элементов, полученных с помощью генераторов случайных чисел. После многократного повторения этой процедуры строится гистограмма для определяющего параметра системы.
