Расчетно-графическая работа №1. Определение равнодействующей плоской системы сходящихся сил аналитическим способом

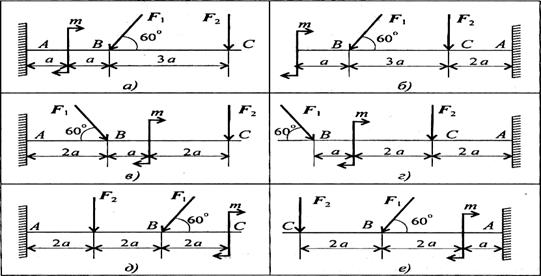
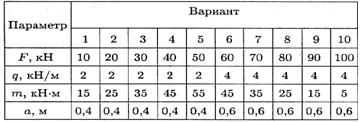
Задача 1.Определить реакции стержней, удерживающих грузы F₁ и F₂. Массой стержней пренебречь. Схему своего варианта см. на рисунке. Числовые данные своего варианта взять из таблицы

Практическое занятие №2. Плоская система произвольно расположенных сил

Знать теорему Пуансо о приведении силы к точке.

Уметь приводить произвольную плоскую систему сил к точ­ке, определяя величины главного вектора и главного момента сис­темы.

Знать три формы уравнений равновесия и уметь ими пользо­ваться при определении реакций в опорах балочных систем.

Основные формулы и предпосылки расчета

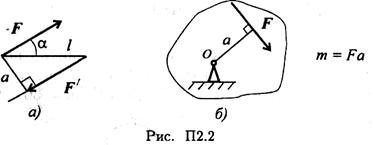
Виды опор балок и их реакции (рис. П2.1)

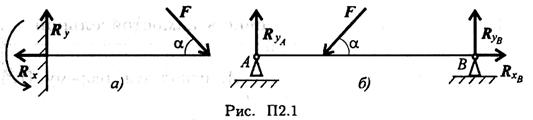
Моменты пары сил и силы относительно точки (рис. П2.2)

Главный вектор

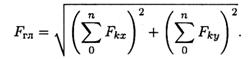
Главный момент

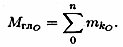
Условия равновесия

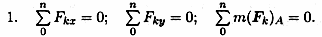
Проверка:

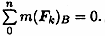
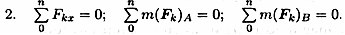
Проверка:

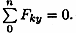
Расчетно-графическая работа №2. Определение реакций в опорах балочных систем под действием сосредоточенных сил и пар сил

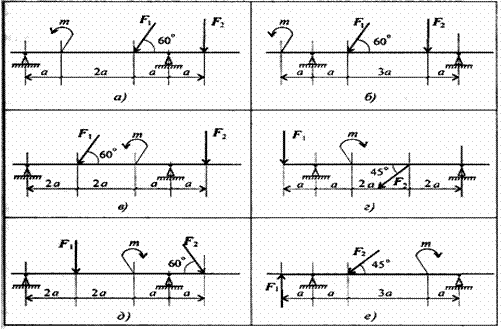
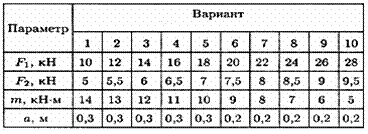
Задание 1. Определить величины реакций в опоре защемлен­ной балки. Провести проверку правильности решения.

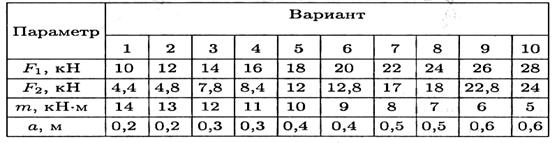
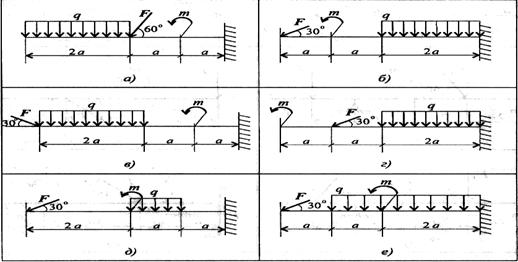
Задание 3. Определить величины реакций в шарнирных опорах балки. Провести проверку правильности решения.

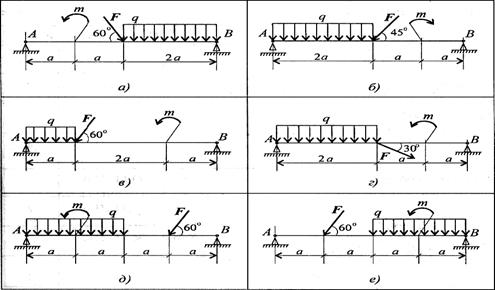
Практическое занятие 3. Центр тяжести.

Знать методы определения центра тяжести тела и плоских сечений, формулы для определения положения ЦТ плоских сечений.

Уметь определять положение центра тяжести сложных гео­метрических фигур, определять положение центра тяжести фи­гур, составленных из стандартных профилей.

Основные формулы и предпосылки расчета

Центры тяжести простейших сечений (рис. П3.1)

Геометрические характеристики стандартных прокатных про­филей в Приложении 2. Методы расчета:

1. метод симметрии;
2. метод разделения на простые части;
3. метод отрицательных площадей.

Координаты центров тяжести сложных и составных сечений:

где A_k— площади частей сечения; x_k, у_k — координаты ЦТ частей сечения; А — суммарная площадь сечения,

Пример1. Определить положение центра тяжести фигуры, представленной на рис. 8.4.

Решение

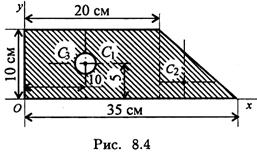Разбиваем фигуру на три части:

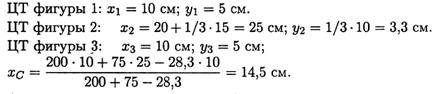
Аналогично определяется у_С = 4,5 см.

Пример 2. Определить координаты центра тяжести составного сечения. Сечение состоит из листа и прокатных профилей (рис. 8.5).

Примечание. Часто рамы сваривают из разных профилей, создавая необходимую конструкцию. Таким образом, уменьшается расход металла и образуется конструкция высокой прочности.

Для стандартных прокатных профилей собственные геометри­ческие характеристики известны. Они приводятся в соответствую­щих стандартах.

Решение

1. Обозначим фигуры номерами и выпишем из таблиц необхо­димые данные:

1 — швеллер № 10 (ГОСТ 8240-89); высотаh = 100 мм; ширина полкиb = 46 мм; площадь сечения А₁ = 10,9 см²;

2 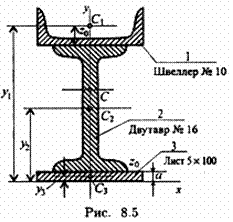— двутавр № 16 (ГОСТ 8239-89); высота 160 мм; ширина полки 81 мм; площадь сечения А₂ — 20,2 см²;

3 — лист 5x100; толщина 5 мм; ширина 100мм; площадь сечения A₃ = 0,5 • 10 = 5 см².

2. Координаты центров тяжести каждой фигуры можно опреде­лить по чертежу.

Составное сечение симметрично, поэтому центр тяжести нахо­дится на оси симметрии и координата х_С = 0.

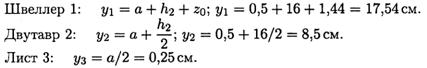
3. Определение центра тяжести составного сечения:

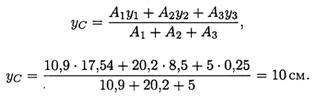
Пример 3. Определить координаты центра тяжести сечения, по­казанного на рис. 8, а. Сечение состоит из двух уголков 56x4 и швеллера № 18. Выполнить проверку правильности определения положения центра тяжести. Указать его положение на сечении.

Решение

1. Разобьем сечение на профили проката: два уголка 56 х 4 и швеллер № 18. Обозначим их 1, 2, 3 (см. рис. 8, а).

2. Укажем центры тяжести каждого профиля, используя табл. 1 и 4 прил. I, и обозначим их С₁, С₂, С₃.

3. Выберем систему координатных осей. Осьу совместим с осью симметрии, а ось х проведем через центры тяжести уголков.

4. Определим координаты центра тяжести всего сечения. Так как осьу совпадает с осью симметрии, то она проходит через центр тяжести сечения, поэтомух_с = 0. Координату у_с опреде­лим по формуле

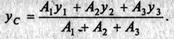
Пользуясь таблицами приложения, определим площади каждого профиля и координаты центров тяжести:

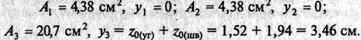
Координаты у₁ и у₂равны нулю, так как ось х проходит через центры тяжести уголков. Подставим полученные значения в формулу для определения у_с:

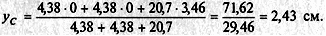
5. Укажем центр тяжести сечения на рис. 8, а и обозначим его буквой С.Покажем расстояниеу_С= 2,43 см от оси х до точ­ки С.

Поскольку уголки симметрично расположены, имеют одина­ковую площадь и координаты, то А₁ = А₂, у₁ = у₂. Поэтому фор­мула для определенияу_С может быть упрощена:

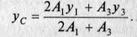
6. Выполним проверку.Для этого ось х проведем по нижнему краю полки уголка (рис. 8, б). Осьу оставим, как в первом ре­шении. Формулы для определениях_С иу_С не изменяются:

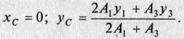
Площади профилей останутся такими же, а координаты центров тяжестей уголков и швеллера изменятся. Выпишем их:

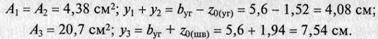
Находим координату центра тяжести:

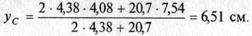
По найденным координатамх_с и у_снаносим на рисунок точ­ку С. Найденное двумя способами положение центра тяжести находится в одной и той же точке. Проверим это. Разница между координатами у_с, найденными при первом и втором решении, составляет: 6,51 - 2,43 = 4,08 см.

Это равно расстоянию между осями х при первом и втором решении: 5,6 - 1,52 = 4,08 см.

Ответ: у_с = 2,43 см, если ось х проходит через центры тяже­сти уголков, или у_с = 6,51 см, если ось х проходит по нижнему краю полки уголка.