Тема 5. «Решение систем линейных уравнений методом Крамера».
Число: 2085
Определение 1.Определитель называется главным, если составлен из коэффициентов при неизвестных. Алгоритм решения систем уравнений методом Крамера 1). Вычислить главный определитель ( 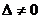 ) )  2) Найти определители 2) Найти определители 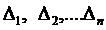 , где , где 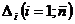 получается из главного определителя путём замены i-го столбца столбцом свободных членов системы. 3) Найти неизвестные по формулам: получается из главного определителя путём замены i-го столбца столбцом свободных членов системы. 3) Найти неизвестные по формулам: 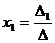 , , 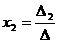 …., …., 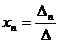 Пример 1. С помощью формул Крамера найти решение системы линейных уравнений Пример 1. С помощью формул Крамера найти решение системы линейных уравнений 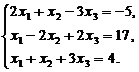 (1) Решение. Вычислим главный определитель системы (1) Решение. Вычислим главный определитель системы 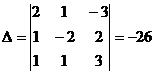 Так как Δ ≠ 0, то решение системы может быть найдено по формулам Крамера. Для этого найдем Так как Δ ≠ 0, то решение системы может быть найдено по формулам Крамера. Для этого найдем 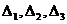 : : 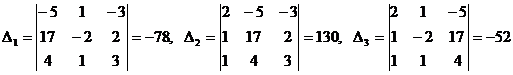 . Подставляя найденные значения определителей в формулы Крамера, получим искомое решение системы: . Подставляя найденные значения определителей в формулы Крамера, получим искомое решение системы: 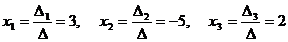 . Ответ: (3; -5; 2) . Ответ: (3; -5; 2) |
Тема 6. «Нахождение обратной матрицы»
 Определение 1.Матрица Определение 1.Матрица 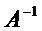 называется обратной матрице А, если выполняется условие: называется обратной матрице А, если выполняется условие: 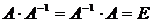 ( Е – единичная матрица) Определение 2. Квадратная матрица называется невырожденной, если её определитель не равен нулю ( Если ( Е – единичная матрица) Определение 2. Квадратная матрица называется невырожденной, если её определитель не равен нулю ( Если 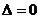 , то матрица вырожденная). , то матрица вырожденная).  Теорема: Если матрица невырожденная, то она имеет обратную матрицу, которая находится по формуле: Теорема: Если матрица невырожденная, то она имеет обратную матрицу, которая находится по формуле: 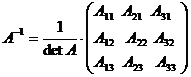 , где , где 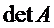 - определитель матрицы А, - определитель матрицы А, 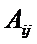 - алгебраические дополнения ( i- номер строки, j- номер столбца). Алгоритм решения: 1) Вычислить определитель матрицы - алгебраические дополнения ( i- номер строки, j- номер столбца). Алгоритм решения: 1) Вычислить определитель матрицы 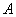 . 2) Найти алгебраические дополнения 3) Составить матрицу алгебраических дополнений к элементам матрицы 4) Транспонировать матрицу алгебраических дополнений. 5) Каждый элемент матрицы разделить на . 2) Найти алгебраические дополнения 3) Составить матрицу алгебраических дополнений к элементам матрицы 4) Транспонировать матрицу алгебраических дополнений. 5) Каждый элемент матрицы разделить на 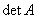 . Полученная матрица и будет обратной к исходной. 6) Проверка. . Полученная матрица и будет обратной к исходной. 6) Проверка. 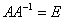 . Пример 1. Найдите обратную матрицу . Пример 1. Найдите обратную матрицу 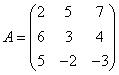 и выполните проверку: Решение:1) Найдём определитель матрицы А: и выполните проверку: Решение:1) Найдём определитель матрицы А:  2) Вычислим алгебраические дополнения: 2) Вычислим алгебраические дополнения: 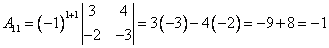 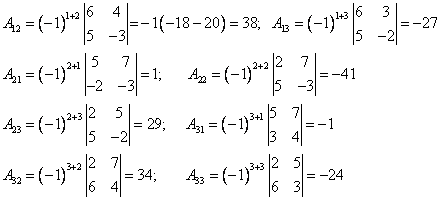 3) Составим матрицу алгебраических дополнений 3) Составим матрицу алгебраических дополнений 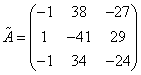 4) Транспонируем матрицу алгебраических дополнений. 4) Транспонируем матрицу алгебраических дополнений. 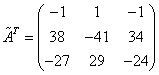 5) Каждый элемент матрицы разделим на 5) Каждый элемент матрицы разделим на 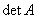 . Полученная матрица и будет обратной к исходной. . Полученная матрица и будет обратной к исходной. 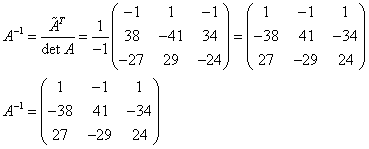 6) Проверка. 6) Проверка. 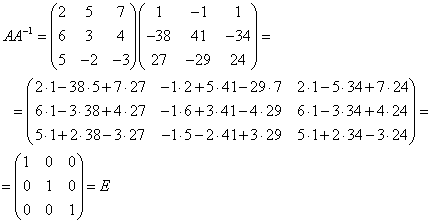 |
Тема 7. «Решение систем в матричной форме».
Алгоритмрешения систем в матричной форме: 1) Записать систему уравнений в матричном виде : АХ=В, где А-матрица коэффициентов перед неизвестными, Х – матрица-столбец неизвестных, В- матрица-столбец свободных членов 2) Найти обратную матрицу 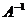 . .  3) Найти неизвестные по формуле: 3) Найти неизвестные по формуле: 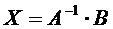 Пример 1.Решите систему уравнений Пример 1.Решите систему уравнений 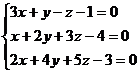 в матричной форме. Решение: Запишем систему иначе: в матричной форме. Решение: Запишем систему иначе: 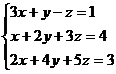 , где , где 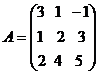 , , 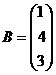 Найдем Найдем 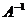 , для этого вычислим определитель: , для этого вычислим определитель:  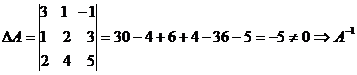 существует. существует. 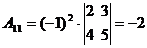 , , 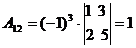 , , 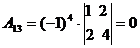 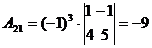 , , 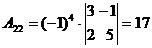 , , 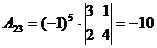 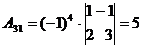 , , 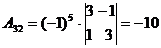 , , 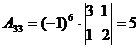 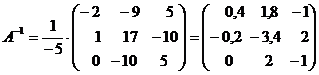 . . 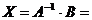 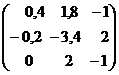 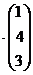 = = 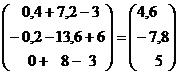 Проверка: Проверка: 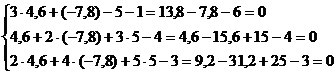 Ответ: (4,6; -7,8; 5). Ответ: (4,6; -7,8; 5). |
ОБРАЗЕЦ выполнения контрольной работы « Линейная алгебра».
Решить систему уравнений 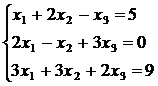
а) методом Гаусса, б) методом Крамера, в) в матричной форме.
А) Метод Гаусса: 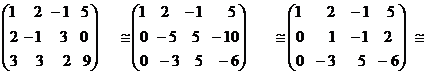
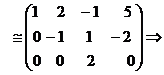
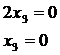
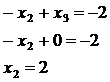
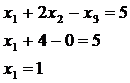
Ответ: (1; 2; 0)
б) Метод Крамера: Вычислим главный определитель( из коэффициентов при х)
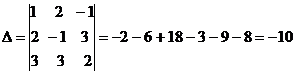
Заменяем в главном определителе первый, (второй, третий) столбик столбцом свободных коэффициентов, получим: 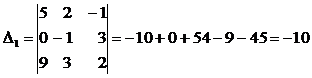
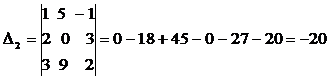 .
. 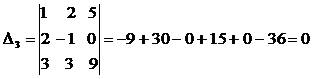 .
. 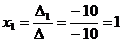 ,
, 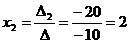 ,
, 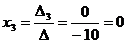 .
.
Ответ: (1; 2; 0).
в) В матричной форме: 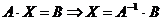 , где
, где 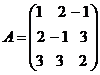 ,
, 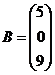
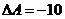 .
. 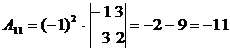 ,
, 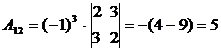
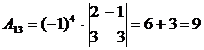 ,
, 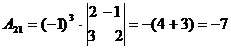 ,
, 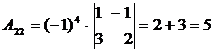
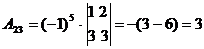 ,
, 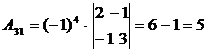 ,
, 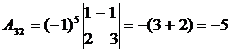
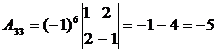 .
. 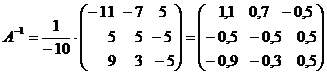
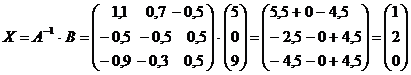 . Ответ: (1; 2; 0)
. Ответ: (1; 2; 0)
РАЗДЕЛ 7. «Основы аналитической геометрии».
