О вычислении констант равновесия

Константы равновесия 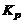могут быть определены или расчетом по формуле (1.3.21), или опытным путем – по результатам замеров парциальных давлений газов, находящихся в состоянии химического равновесия (см. (1.3.20)).

В ряде случаев удобно константы равновесия некоторых реакций вычислять по константам равновесия других реакций. Так, например, для реакций диссоциации углекислого газа:

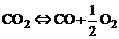, (1.4.1)

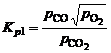(1.4.2)

и диссоциации паров воды:

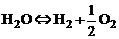, (1.4.3)

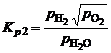, (1.4.4)

протекающих одновременно в смеси, будет наблюдаться их взаимное влияние. Совместное протекание этих реакций легче исследовать, если составить суммарную реакцию

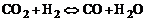, (1.4.5)

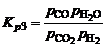. (1.4.6)

Константа равновесия суммарной реакции, называемой реакцией водяного пара, равна:

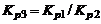. (1.4.7)

Особенностью этой реакции является то, что она проходит без изменения числа молей (объема). Следовательно, состав продуктов сгорания, если они образуются в соответствии с этой реакцией, не зависит от давления.

Уравнение реакции водяного пара используется при проведении расчетов равновесных состояний.

Константа равновесия 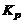гетерогенных систем.Формулы (1.3.20) и (1.3.21) для констант равновесия 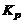были введены для гомогенных химических систем, состоящих из газов.

Рассмотрим теперь условия химического равновесия гетерогенных систем, состоящих из газов, твердых веществ и жидкостей. Примером реакции, протекающей в такой системе, является реакция сжигания графита Св атмосфере кислорода :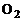

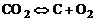. (1.4.8)

На основе современных представлений о механизме протекания таких реакций предполагается, что они проходят следующим образом.

Над твердыми и жидкими веществами гетерогенных систем в результате испарения и сублимации находятся насыщенные пары этих веществ. Эти пары имеют парциальные давления, зависящие только от температуры, и находятся в равновесном состоянии с веществами, из которых они образовались. Убыль пара в газообразной фазе, вступившего в химическую реакцию, будет пополняться дополнительным испарением жидкости или дополнительной сублимацией твердых тел. В результате этого парциальные давления насыщенных паров жидких и твердых тел будут, несмотря на реакцию, оставаться постоянными при постоянной температуре смеси. Так как в данном случае реакция протекает между газообразными веществами, то формулы (1.3.20) и (1.3.21) остаются справедливыми и для гетерогенных веществ.

В соответствии с изложенным реакцию (1.4.8) можно представить в виде

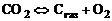. (1.4.9)

при этом константа равновесия будет равна:

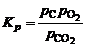, (1.4.10)

где давление 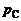при постоянной температуре также будет оставаться постоянным.

Константа равновесия 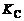. Введем понятие объемно-моль-ной концентрации. Под объемно-мольной концентрацией i-го газа 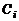понимается число молей i-го газа в единице объема. Тогда

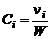. (1.4.11)

Концентрации 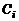отдельных газов, образующих смесь, будут пропорциональны парциальным давлениям этих газов. Это утверждение следует из (1.2.7), (1.2.8), (1.1.7), (1.2.27). Так как 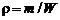, то уравнение состояния для i-й газовой компоненты имеет вид

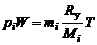. (1.4.12)

Учитывая соотношение (1.4.11) и равенство 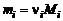, получим

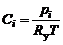. (1.4.13)

Формула (1.4.13) показывает, что объемно-мольная концентрация газа пропорциональна его парциальному давлению.

Константа равновесия 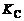, устанавливающая связь объемно-мольных концентраций компонентов, участвующих в химической реакции, может быть выражена через константу равновесия 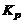. Согласно формуле (1.4.13),

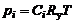. (1.4.14)

Подставляя значения парциальных давлений, связанных с концентрациями 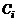соотношением (1.4.14), в (1.3.20), получим

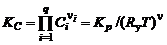, (1.4.15)

где 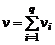– суммарное количество молей газа в смеси.

Диссоциация. Влияние давления на степень диссоциации. Распад химического соединения на более простые вещества, которыми в частном случае могут быть химические элементы, называется диссоциацией.

Исследуем влияние давления на степень диссоциации на примере двухатомного газа. Пусть это будет кислород. Реакция диссоциации кислорода записывается в виде

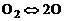. (1.4.16)

Обозначим через 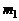массу атомарного кислорода О,а через 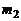массу молекулярного кислорода 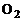и примем, что суммарная масса равна единице:

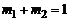. (1.4.17)

Степень диссоциации bопределяется как отношение

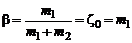. (1.4.18)

Далее воспользуемся соотношением

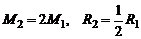. (1.4.19)

Тогда давление смеси будет равно:

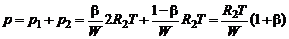. (1.4.20)

В соответствии с законом действующих масс,

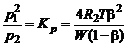. (1.4.21)

Подставляя в последнее соотношение давление смеси
(см. (1.4.20)), получим

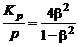. (1.4.22)

Формула (1.4.22) показывает, что с ростом давления степень диссоциации b уменьшается. В табл. 1.1 приведены значения b для реакции диссоциации кислорода при различных давлениях смеси, которые это иллюстрируют.

Т а б л и ц а 1.1

T=3000 K	T=3500 K
р, ата	b	р, ата	b
	0.060		0.251
	0.019		0.082
	0.006		0.026

В общем случае справедливы утверждения:

· в реакциях, происходящих с увеличением числа молей, при возрастании давления степень диссоциации уменьшается;

· в реакциях, происходящих без изменения числа молей, степень диссоциации не зависит от давления.

1.5. Основные сведения, связанные с описанием химически
и термодинамически неравновесных систем

Если внешние условия меняются достаточно быстро, то в системе не успевает установиться химическое равновесие. В этом случае скорости прямой и обратной реакций не равны и их нужно рассматривать совместно.

Например, для реакции диссоциации молекулярного кислорода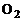

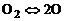(1.5.1)

в неравновесной системе при определении состава смеси следует учитывать скорости как прямой:

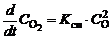, (1.5.2)

так и обратной реакций:

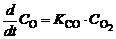, (1.5.3)

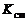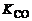где коэффициенты пропорциональности и , зависящие от температуры смеси, называются соответственно константами скоростей прямой и обратной реакций.

Уравнения для скоростей химических реакций называются уравнениями кинетики.

С течением времени скорости прямой и обратной реакций уравниваются и при переходе к состоянию равновесия выполняется условие

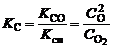. (1.5.4)

Отличительная особенность расчета химически неравновесных процессов состоит в том, что скорость образования отдельных компонентов зависит от стадий химических превращений, в которых участвуют эти компоненты. Это означает, что, определяя текущий состав смеси, следует учитывать все химические реакции, которые в ней могут проходить. Наиболее полная информация по составу в каждой точке турбулентной струи, температурам, скоростям и прочим газодинамическим параметрам выдается при непосредственном расчете турбулентной струи с учетом уравнений кинетики. Методы совместного решения стационарных двумерных уравнений пограничного слоя с уравнениями кинетики разработаны достаточно хорошо. Однако практическая реализация расчета химически неравновесных турбулентных струй ограничена, главным образом, отсутствием надежных данных по скоростям химических реакций. Например, приведем результаты расчета скоростей реакции горения СО(это основное химическое соединение в составе продуктов сгорания большинства топлив, догорающее в атмосфере) при Т=2100 K, 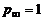ата, в предварительно подготовленной смеси СО с воздухом (содержание СОпо объему – 40%) по различным методикам:

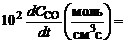5.7; 4.1; 0.001; 0.26; 8.9; 1.7.

Экзотермические и эндотермические реакции. Химические реакции обычно происходят с выделением или поглощением тепла.

Реакции, сопровождающиеся выделением тепла, называются экзотермическими. Примеры экзотермических реакций:

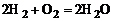, (1.5.5)

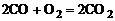. (1.5.6)

Реакции, сопровождающиеся поглощением тепла, называются эндотермическими. Примером эндотермической реакции является реакция диссоциации :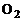

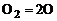, (1.5.7)

а также реакции, обратные приведенным в соотношениях (1.5.5), (1.5.6).

Влияние температуры на скорость реакции. Запишем в общем виде выражение для скорости прямой реакции :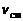

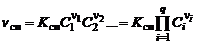, (1.5.8)

где 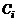– объемно-мольная концентрация, 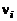– число молей i-го газа, вступающего в реакцию.

Все рассуждения и выводы, приведенные далее, будут справедливы и для обратной реакции. Поэтому ограничимся анализом лишь прямой реакции.

В соотношение (1.5.8) входит константа скорости прямой реакции 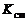. Расчеты и опытные данные показывают, что значение 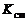, а, следовательно, и скорость реакции при увеличении температуры растут очень быстро.

Установим зависимость между значениями 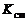и T на базе молекулярно-кинетической теории.

Основным условием для прохождения реакции является столкновение молекул газа, участвующих в ней. По этому скорость реакции будет тем больше, чем чаще сталкиваются молекулы, а следовательно, чем больше будут концентрации реагирующих веществ. Однако далеко не каждое столкновение молекул заканчивается их соединением и образованием новых компонентов. Это связано с тем, что энергия сталкивающихся молекул должна быть достаточной для разрушения старых химических связей и образования новых.

Тот минимум энергии, который необходим для обеспечения химического взаимодействия сталкивающихся молекул, называется энергией активации. Обозначим ее буквой А.

При увеличении температуры увеличиваются скорость хаотического теплового движения молекул и их кинетическая энергия, что влечет за собой увеличение числа столкновений активных молекул и, следовательно, скорости химической реакции.

Согласно кинетической теории газа число столкновений, энергия которых превышает энергию активации, будет равно:

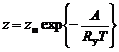, (1.5.9)

где z –число столкновений, энергия которых превышает А;
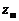– полное число столкновений. В соответствии с этим зависимость константы скорости реакции 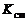от температуры будет иметь вид

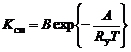, (1.5.10)

где В – константа скорости, соответствующая полному числу столкновений.

Вследствие сильной зависимости скорости реакции от температуры многие из них (например, соединение 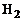и 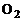) при низких температурах протекают столь медленно, что состав смеси остается неизменным или, как это принято говорить, «замороженным». При высоких температурах эти же реакции, наоборот, осуществляются со столь большими скоростями, практически бесконечно большими, что смесь мгновенно переходит в равновесное состояние.

Если реакция между компонентами, составляющими смесь, экзотермическая, то с увеличением температуры и, соответственно, скорости увеличивается количество тепла, выделяющегося в реакции. Это в свою очередь приведет к дальнейшему росту температуры. Процесс становится лавинообразным. Смесь воспламеняется и сгорает.

Температура, при которой количество выделяющейся при реакции теплоты начинает превышать тепловые потери, что приводит к быстрому увеличению температуры, называется температурой воспламенения.

Смесь некоторых газов способна самовоспламеняться на воздухе при обыкновенной температуре.

Проведенный анализ позволяет предположить, что турбулентные струи, в которых возможно протекание экзотермических реакций при смешении с окружающим воздухом, будут либо «замороженными», либо равновесными.

Помимо химической возможна и термодинамическая неравновесность. Например, в плазме электроны, имеющие значительно меньшую массу по сравнению с ионами, быстрее реагируют на изменение внешних условий. Поэтому температура электронов при термодинамической неравновесности может существенно отличаться от температуры ионов.

1.6. Определение равновесного состава и термодинамических характеристик смеси газов при заданных давлении
и температуре

Определение состава и термодинамических характеристик равновесной смеси при заданных условной формуле смеси, давлении р и температуре T проводится при следующих основных допущениях:

· смесь реагирующих газов является равновесной;

· статическое давление смеси равняется, по закону Дальтона, сумме парциальных давлений газообразных компонентов;

· уравнение состояния для идеального газа справедливо как для отдельных газообразных компонентов, так и для смеси в целом;

· константы равновесия реакций зависят только от температуры;

· объем, занимаемый твердой фазой, пренебрежимо мал по сравнению с объемом, занимаемым газообразными продуктами;

· температуры твердой и газовой фаз равны. Парциальное давление газовой фазы равно давлению насыщенного пара для данного конденсированного химического соединения.

В соответствии с законом, установленным в 1840 г. русским академиком Г.Г. Гессом, тепловой эффект реакции не зависит от пути реакции при сохранении постоянными начальных и конечных условий. Это позволяет цепочку химических реакций, приводящих к образованию конечных компонентов, выбирать произвольно, исходя из удобства разработки алгоритма расчета.

В большинстве существующих программ термодинамических расчетов используется система реакций диссоциации конечных компонентов на атомы.

Тогда полная система уравнений для определения равновесного состава запишется в следующем виде.

Уравнение диссоциации всех ожидаемых молекулярных компонентов 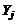на атомы :

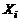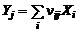, (1.6.1)

где 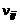– число атомов i-го химического элемента в компоненте j.

Закон действующих масс для неконденсированных веществ:

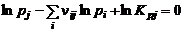, (1.6.2)

где 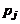и 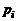– парциальные давления молекулярных и атомарных компонентов, а 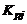– зависящая от температуры константа равновесия j-й реакции.

Закон действующих масс для газовой фазы конденсированных веществ:

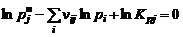, (1.6.3)

где 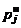– давление насыщенного пара для данного конденсированного химического соединения. При фиксированной температуре величины 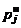известны.

Уравнения сохранения вещества, представляющие собой условия постоянства количества молей i-го химического элемента в процессе реакции:

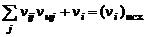, (1.6.4)

где 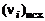– число молей i-го химического элемента в исходных продуктах, а 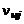и 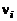– числа молей молекулярных и атомарных компонентов. По закону Авогадро моли различных идеальных газов при одинаковых условиях занимают одинаковый объем. Это позволяет связать 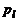и 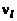соотношениями вида (см. (1.2.10) и (1.2.30)):

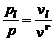, (1.6.5)

где 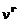– общее число молей газа, 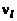– число молей l-го компонента газовой смеси, 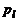– парциальное давление l-го компонента.

Закон Дальтона для газообразных компонентов:

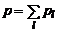. (1.6.6)

Общее количество молей конденсированного вещества 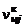складывается из числа молей в газовой 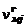и твердой 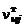фазах:

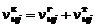. (1.6.7)

Аналогично для конденсированных элементов

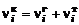. (1.6.8)

Число молей i-го химического элемента в исходных продуктах выражается через условную формулу смеси 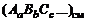и массу т в кг :

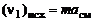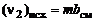, и т.д. (1.6.9)

Если обозначить через 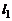– число газообразных веществ, 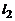– число газообразных элементов, 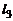– число конденсированных веществ, 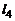– число конденсированных элементов, то можно написать 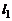уравнений (1.6.2), 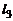– (1.6.3), 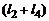– (1.6.4), 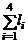– (1.6.5), 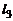– (1.6.7), 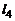– (1.6.8). В результате будем иметь замкнутую систему (1.6.2) – (1.6.9) для определения т, парциальных давлений газообразных продуктов и молярного состава смеси. Массовые доли выражаются через молярный состав (см. (1.2.11)):

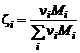. (1.6.10)

Если в смеси имеют место процессы ионизации, то система (1.6.2) – (1.6.9) дополняется уравнениями, выражающими закон действующих масс применительно к ионизации, которые формально могут быть записаны в форме (1.6.2), и условием сохранения заряда системы.

Система (1.6.2) – (1.6.9) решается численно методом последовательных приближений.

Рассмотренный выше порядок нахождения равновесного состава обладает универсальностью, так как введение нового химического соединения добавляет к системе (1.6.1) лишь одну реакцию диссоциации этого соединения на атомы. Однако для конкретных исходных веществ могут быть построены более простые и наглядные, но, естественно, менее универсальные схемы расчета равновесного состава.

В уравнениях, описывающих процесс развития турбулентной струи, применяются такие термодинамические величины: 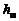– теплосодержание (энтальпия), R – газовая постоянная, 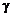– показатель адиабаты. Эти параметры определяются по соотношениям (1.2.40) – (1.2.46).