Построение эпюр Q и М при изгибе.

Изгиб вызывается действием сил, направленных перпендикулярно оси бруса, или пар сил, лежащих в плоскости симметрии поперечного сечения.

Брус, работающий на изгиб, называется балкой. На балку действуют внешние силы и реакции опор.

Под действием внешних сил в балке возникают: поперечная сила Q и изгибающий момент М.

Поперечная сила в сечении равна алгебраической сумме проекции на ось, перпендикулярную оси балки, всех внешних сил, расположенных по одну сторону от сечения.

Поперечная сила положительна, если она вращает отсечённую часть балки относительно сечения по часовой стрелке.

Изгибающий момент в сечении равен алгебраической сумме моментов всех внешних сил, расположенных по одну сторону от сечения, относительно центра тяжести сечения.

Изгибающий момент положителен, если он растягивает нижние волокна.

Поперечная сила и изгибающий момент изменяются по длине балки. Графики изменения поперечной силы и изгибающего момента по длине балки, называются эпюрами.

Положительные значения эпюры Q откладываются вверх от базисной линии, а положительные значения эпюры М откладываются ниже базисной линии, т.е. эпюра М строится со стороны растянутого при изгибе волокна.

Основные правила при построении эпюр.

1. На ненагруженных участках (участок ВС, рис.25) эпюра Q постоянна, представляет собой прямую, параллельную оси балки, а эпюра М – наклонную прямую.

2. На участках с равномерно распределённой нагрузкой эпюра Q – наклонная прямая, а эпюра М – квадратная парабола, обращённая выпуклостью в сторону действия нагрузки (участок АВ, рис.25).

3. В сечении балки Z = 2 м, где поперечная сила Q при непрерывном изменении проходит через нулевое значение, меняя знак, на эпюре М будет вершинка параболы (экстремальное значение) (сечение Z, рис.26).

4. В сечении под сосредоточенной силой F эпюра Q имеет скачок, равный приложенной силе, а эпюра М – излом, острие которого обращено в сторону действия силы (сечение Д, рис.27).

5. В сечении, где приложен сосредоточенный момент m (сечение С, рис.27) эпюра М имеет скачок, равный значению этого момента. Эпюра Q проходит через указанное сечение без изменения.

Усвоив основные правила, переходим к построению эпюр Q и М.

Решение балок с защемлённым концом ведём без предварительного определения усилий в защемлении, начиная со свободного конца.

Пример 5.1.

Построить эпюры Q и М для балки, изображённой на рис.25а.

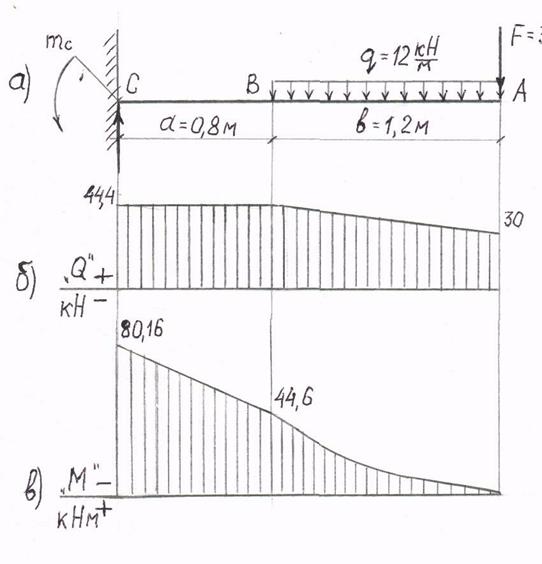рис. 25

Решение:

1) Строим эпюру Q.

Идём со свободного конца. Имеем два участка: АВ – участок с равномерно распределённой нагрузкой, ВС – ненагруженный участок.

На участке с равномерно распределённой нагрузкой эпюра Q – наклонная прямая, поэтому необходимо определить значения Q в начале участка и в конце участка АВ.

Q_A^лев = +F = +30 кН

Q_A^пр = F + q ^. b = 30 + 12 ^. 1,2 = 44,4 кН

На ненагруженном участке ВС эпюра Q постоянна. Значит, достаточно определить одно значение Q в любом сечении на участке ВС.

Q_ВС = F + q ^. b = 30 + 12 ^. 1,2 = 44,4 Кн

Проводим нулевую (базовую) линию под изображением балки и от неё в принятом масштабе откладываем найденные значения поперечных сил с учётом знаков с соответствующих точках (рис.25б).

2) Строим эпюру М по характерным точкам. Характерные точки для данной балки - граничные точки участков.

М_А = 0 (сила F проходит через точку А, момента не даёт)

М_В = -F ^. b – q ^. b 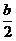^. = -30 ^. 1,2 – 12 ^. 1,2 ^. 0,6 = -44,6 кНм

М_С = -F ^. (a + b) – q ^. b ^. (a + 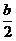) = -30 ^. 2 – 12 ^. 1,2 ^. 1,4 = -80,16 кНм

На участке АВ эпюра М очерчивается параболой, на ненагруженном участке ВС эпюра М идёт по наклонной линии (рис.25в). Эпюра М откладывается выше базисной линии (растянуты верхние волокна).

3) Определение усилий в защемлении.

Положительная эпюра Q свидетельствует о том, что реактивная сила V_C = Q_C = 44,4 кН направлена вверх.

Реактивный момент m_с направлен против хода часовой стрелки согласно характеру деформирования балки.

4) Опасным является сечение С, где действует максимальный по абсолютной величине изгибающий момент - М_МАХ = 80,16 кНм.

Пример 5.2.

Построить эпюры Q и М для балки, изображённой на рис.26а.

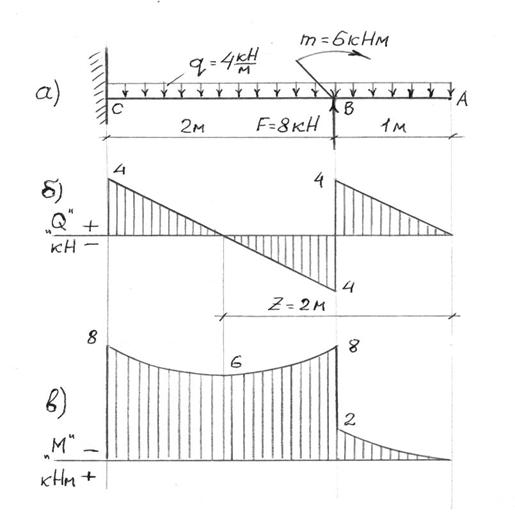
рис.26

Решение:

1) Строим эпюру Q.

Идём со свободного конца. Имеем два загруженных участка АВ и ВС. На каждом из участков надо определить два значения поперечной силы Q – в начале участка и в конце.

Перемещаясь от правого свободного конца балки, находим:

Q_A =0

Q_B^пр = q ^. 1 = 4 ^. 1 = 4 кН

Q_B^лев = q ^. 1 – F = 4 ^. 1 – 8 = -4 кН

Q_C = q ^. 3 – F = 4 ^. 3 – 8 = 4 Кн

От базовой линии в принятом масштабе откладываем найденные значения поперечных сил с учётом знаков (рис.26б).

Как видно из эпюры Q, в сечении Z поперечная сила Q при непрерывном изменении проходит через нулевое значение, меняя знак. Определим значение абсциссы Z, при котором Q = 0.

QZ = 0   QZ = -F + q . Z

Отсюда: -F + q ^. Z = 0

q ^. Z = F

Z = 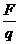= = 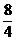2 м

2) Строим эпюру М по характерным точкам (см. пример 5.1.).

М_А = 0

Там, где приложен сосредоточенный момент m, ордината эпюры М должна скачком меняться в соответствии со значением этого момента. Поэтому надо брать сечения слева и справа от этого момента m.

M_B^пр = -q ^. 1 ^.0,5 = -4 ^. 1 ^. 0,5 = -2 кНм

М_В^лев = -q ^. 1 ^. 0,5 – m = -4 ^. 1 ^. 0,5 – 6 = -8 кНм

М_С = -q ^. 3 ^. 1,5 + F ^. 2 – m = -4 ^. 3 ^. 1,5 + 8 ^. 2 – 6 = 8 кНм

Необходимо определить момент в сечении с абсциссой Z = 2 м.

М_Z = -q ^. 2 ^. 1 + F ^. 1 – m = -4 ^. 2 ^. 1 + 8 ^.1 – 6 = -6 кНм (вершинка параболы).

Растянуты верхние волокна – эпюра М откладывается выше базисной линии (рис. 26в).