Пояснительная записка по выполнению контрольных работ
По технической механике студенты выполняют одну контрольную работу.
Контрольная работа включает в себя выполнение пяти задач по теоретической механике и сопротивлению материалов.
К каждой задаче дается 10 схем и таблицы (с тем же номером, что и задача).
Студент во всех задачах, кроме задачи № 3, выбирает номер схемы по последней цифре шифра, а номер строки в таблице по предпоследней цифре шифра. Например, если шифр оканчивается числом 09, то берут 9 схему и данные по строке 0 из таблиц.
Вариант задачи № 3 определяется по двум последним цифрам шифра. Каждому варианту задачи № 3 соответствуют указанная в таблице схема и размеры сечения (см. табл. 3).
Каждая контрольная работа выполняется в отдельной ученической тетради в клетку. На обложке тетради разборчиво пишется наименование учебного заведения, специальность, наименование учебного предмета, номер контрольной работы, номер варианта, фамилия, имя и отчество студента, его шифр и учебная группа.
При выполнении контрольных работ необходимо соблюдать следующие требования:
1. Контрольные работы выполнять строго в соответствии с вариантом студента. В противном случае они не зачитываются и возвращаются для переделки.
2. Решение каждой задачи обязательно начинать на развороте тетради (на четной странице, начиная со второй, иначе работу трудно проверять). Сверху указывается номер задачи, далее делается чертеж и записывается, что в задаче дано и что требуется определить.
3. Чертеж выполняется с учетом условий решаемого варианта задачи: на нем все углы, размеры, силы и их расположение должны соответствовать этим условиям. Кроме того, чертеж должен быть аккуратным и наглядным.
4. Решение задач необходимо сопровождать краткими пояснениями и подробно записывать весь ход расчетов. Записи должны быть четкие, разборчивые.
5. Для всех исходных и вычисленных физических величин должна указываться размерность.
6. На каждой странице оставляют поля шириной 3-4 см. для замечаний рецензента. В конце тетради оставляют несколько чистых страниц для рецензии.
Выполненную контрольную работу необходимо своевременно (согласно учебному графику) выслать в техникум.
После получения зачтенной работы студент должен внимательно изучить рецензию и все замечания преподавателя, обратить внимание на допущенные ошибки, доработать материал.
Незачтенная работа или выполняется заново, или переделывается частично по указанию преподавателя.
Для допуска к экзамену студенту необходимо выполнить все контрольные работы, сделать все необходимые исправления, указанные преподавателем в рецензиях и защитить упомянутые работы, т.е. в процессе опроса по ним показать хорошую осведомленность и самостоятельность выполнения.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
Рекомендуется прочитать общие методические указания, прежде чем приступить к выполнению контрольной работы.
К задаче 1
К решению задачи следует приступать после изучения тем "Основные понятия и аксиомы статики" и "Плоская система сходящихся сил", уяснения приведенных ниже методических указаний и разбора примеров.
В предлагаемой задаче рассматривается тело (узел), находящееся под действием системы сходящихся сил.
Порядок решения задач на систему сходящихся сил следующий:
1. Выбираем узел, который будем рассматривать в равновесии.
2. Рисуем расчетную схему узла, т.е. наносим на него все действующие силы.
3. Записываем систему уравнений равновесия и решаем ее.
При аналитическом методе решения применяемая система двух уравнений равновесие имеет вид:
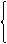 |
SFx = 0
SFy = 0
(Алгебраическая сумма проекций всех сил системы на каждую из координатных осей равна нулю).
Напомним, что проекция силы на ось равна произведению модуля силы на косинус ее острого угла с осью.
Fх = F . Cos α
Проекция положительна, если ее направление совпадает с направлением оси (направление проекции от "а" к "в"), рис.1.
 F1
F1
α F2x= –F2 . Cos α
в а
а в Х
F1x=F1 . Cos α α
F2
рис.1
Пример 1.1
Сила F = 10 кН действует, как показано на рис.2. Найти ее проекции на оси х и у.
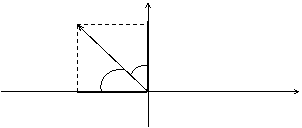 y
y
c
F
300 Fy
600
в Fx о х
рис.2
Решение:
Fx = –F . Cos 600 = –10 . 0,5= –5 кН;
Fу = F . Cos 300 = 10 . 0,87= 8,7 кН.
Запомни!
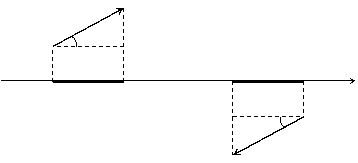
1. Если сила лежит на оси или параллельна оси, то ее проекция равна модулю силы, взятому с соответствующим знаком (рис.3).
2. Проекция силы на перпендикулярную к ней ось равна 0 (рис.4).
F2  F1 в а а в х F1x= –F1 F2x= F2 рис.3 F1 в а а в х F1x= –F1 F2x= F2 рис.3 |  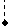  F х Fx = 0 рис.4 F х Fx = 0 рис.4 |
Контрольные вопросы
| Найти проекции силы F на оси, если F = 100 кН (рис5) | ||||||
а) y 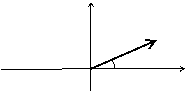 F 150 x F 150 x | Fx = ? (97 кН) Fy = ? (26 кН) cos 150 = 0,97 cos 750 = 0,26 | |||||
б)  y y
  x x F | Fx = ? (71 кН) Fy = ? (–71 кН) cos 450 = 0,71 | |||||
 в) y в) y
800 F | cos 800 = 0,17 cos 100 = 0,98 Fx = ? (–17 кН) Fy = ? (98 кН) | |||||
г)    
F x | cos 50 = 0,99 cos 850 = 0,08 Fx = ? (–99 кН) Fy = ? (+8 кН) | |||||
   д) y F x д) y F x | Fx = ? (100 кН) Fy = ? (0) | |||||
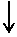 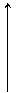  е) y F x е) y F x | Fy = ? (–100 кН) Fx = ? (0) |
рис.5
В задаче ферма опирается на две опоры. Реакция шарнирно-подвижной опоры всегда направлена перпендикулярно опорной плоскости (рис.6).
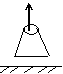 |
V
рис.6
Реакция шарнирно-неподвижной опоры идет по двум направлениям (рис.7).
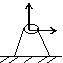 |
V (Вертикальная реакция V,
H горизонтальная H).
рис.7
Внимание:Если нагрузка на балку только вертикальная, то горизонтальная реакция
шарнирно-неподвижной опоры H = 0.
Задача 1.
Определить усилия в стержнях фермы (рис.8) методом вырезания узлов аналитически.
Решение:
Удаляем опоры А и В и заменяем их действие на ферму реакциями (рис.8-б). Так как внешние силы действуют вертикально, то и опорные реакции будут направлены вертикально (НА=0).
Так как нагрузки симметричны относительно опор, то опорные реакции будут равны
VA=VB= 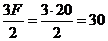 кН.
кН.
Обозначаем узлы фермы буквами, а стержни цифрами (рис.8-б).
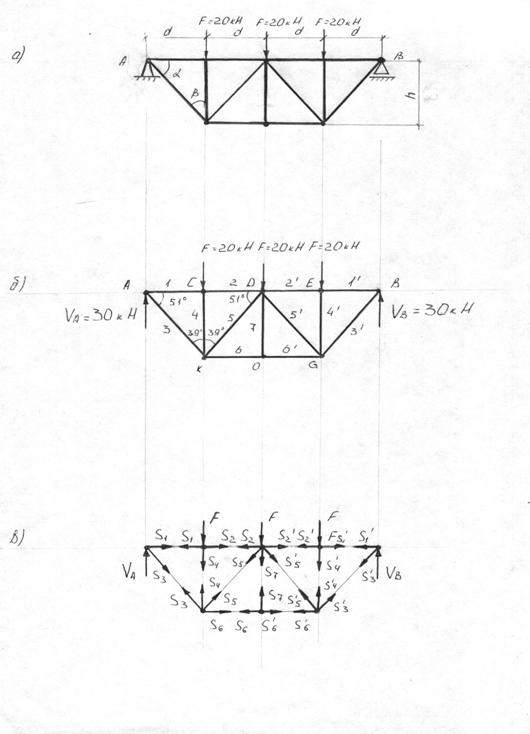 рис.8
рис.8
Каждый узел рассматриваем в равновесии. На узел действует плоская система сходящихся сил. Записываем уравнение равновесия для каждого узла и определяем усилия в стержнях. Вырезание начинаем с того узла, к которому подходят не более двух стержней с неизвестными усилиями. Предполагаем, что все стержни растянуты (растянутые стержни стремятся сжаться, т.е. реакции будут направлены от узлов к центрам стержней). Если в результате вычислений получим реакцию со знаком минус, то это будет указывать на то, что наше предположение неверно, т.е. данный стержень сжат.
Расчетные схемы узлов показаны на рис.8-в. Из схемы фермы (рис.8-а)
tg α = 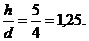
Отсюда, α = 510, cos α = 0,63,
b = 900– α = 390; cos b = 0,78.
Вырезание начинаем с узла А.
Расчетная схема узла А (рис.9)
 y
y
S1
510 х
VA=30 кН 390
S3
рис.9
Условия равновесия
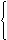 |
 SFx = 0 S1+S3 . cos 510 = 0
SFx = 0 S1+S3 . cos 510 = 0
SFy = 0 VA–S3 . cos 390 = 0
S3 = 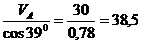 кН
кН
S1 = –S3 . cos 510 = –38,5 . 0,63 = –24 кН (стержень сжат)
Расчетная схема узла С (рис.10).
y
F=20 кН
S1= -24 кН x


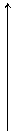
 S2
S2
S4
рис.10
 SFx = 0 S2–S1 = 0
SFx = 0 S2–S1 = 0
SFy = 0 –F–S4 = 0
S2–S1= –24 кН (стержень сжат)
S4= –F= –20 кН (стержень сжат)
Расчетная схема узла К (рис.11)
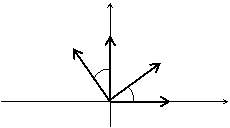 y
y
S4= –20 кН
390
S3=38,5 кН S5
510
S6 x
рис.11
 SFx = 0 S6+S5 . cos 510 –S3 . cos 510= 0
SFx = 0 S6+S5 . cos 510 –S3 . cos 510= 0
SFy = 0 S4+S3 . cos 390 +S5 . cos 390= 0
S5 = 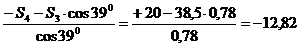 кН (сжат)
кН (сжат)
S6 = –S5 . cos 510 + S3 . cos 510 = +12,82 . 0,63+38,5 . 0,63 = 32 кН
Узел 0. Расчетная схема (рис.12)
 y
y


 S7
S7
x
S6 
рис.12
 SFx = 0
SFx = 0  –S6= 0
–S6= 0
 SFy = 0 S7= 0 стержень 7 при заданном нагружении фермы не работает.
SFy = 0 S7= 0 стержень 7 при заданном нагружении фермы не работает.
 –S6 = 32 кН
–S6 = 32 кН
Усилия в стержнях 1¢, 2¢, 3¢, 4¢ и 5¢ из условий симметрии соответственно равны усилием стержней 1, 2, 3, 4 и 5.
Для контроля правильности вычислений проверим равновесие узла Д (см. рис.8-в)
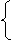
 SFx = 0
SFx = 0 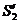 –S2+
–S2+ 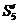 . cos 510–
. cos 510– 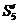 . cos 510 = 0
. cos 510 = 0
SFy = 0 – 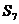 –
– 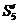 . cos 390 –
. cos 390 – 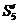 . cos 390 –F = 0
. cos 390 –F = 0
 |
–24– (–24)–12,82 . 0,63 – (–12,82) . 0,63 = 0; 0=0;
–(–12,82) . 0,78– (–12,82) . 0,78–20 = 0; +20–20=0; 0=0.
Составляем таблицу усилий:
| Элементы фермы | Номера стержней | Усилия, кН | |
| "+" растягивающие | "–" сжимающие | ||
| Верхний пояс | 1, 1¢ | –24 | |
| 2, 2¢ | –24 | ||
| Нижний пояс | 6, 6¢ | +32 | |
| Стойки | 4, 4¢ | –20 | |
| Раскосы | 3, 3¢ | 38,5 | |
| 5, 5¢ | –12,82 |
Таблица 1
К задаче 2
К решению задачи следует приступать после изучения тем "Пара сил" и "Плоская система произвольно расположенных сил", усвоения приведенных ниже методических указаний и разбора примеров.
Перед выполнением задачи № 2 студенты должны усвоить следующий материал:
1. Момент силы относительно точки.
2. Условия равновесия произвольной плоской системы сил.
3. Решение аналогичных задач.



 x
x