Раздел 5. Основы теории вероятностей и математической статистики.
В результате изучения раздела студент должен:
знать:
¾ основные понятия комбинаторики;
¾ классическое определение вероятности;
¾ определение случайной величины;
¾ математические характеристики случайной величины: математическое ожидание и дисперсию;
уметь:
¾ решать задачи на нахождение вероятности события;
¾ решать задачи на нахождение математического ожидания и дисперсии случайной величины.
Основные понятия комбинаторики
В разделе математики, который называется комбинаторикой, решаются некоторые задачи, связанные с рассмотрением множеств и составлением различных комбинаций из элементов этих множеств. Например, если взять 10 различных цифр 0, 1, 2, …, 9 и составлять из них комбинации, то будем получать различные числа, например, 345, 534, 1036, 5671, 45 и т.п.
Мы видим, что некоторые из таких комбинаций отличаются только порядком цифр (345 и 534), другие – входящими в них цифрами (1036, 5671), третьи различаются и числом цифр (345 и 45).
Таким образом, полученные комбинации удовлетворяют различным условиям. В зависимости от правил составления можно выделить три типа комбинаций: размещения, перестановки и сочетания. Однако предварительно познакомимся с понятием факториала.
Произведение всех натуральных чисел от 1 до n включительно называют n – факториалом.
1. 
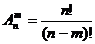Размещения. Размещениями из n элементов по m в каждом называются такие соединения, которые отличаются друг от друга либо самими элементами, либо порядком их расположения.
(1.1),
Пример. Сколько двузначных чисел можно составить из пяти цифр 1, 2, 3, 4, 5 при условии, что ни одна из них не повторяется?
Решение. Так как двузначные числа отличаются друг от друга или самими цифрами, или их порядком, то искомое количество равно числу размещений из пяти элементов по два:
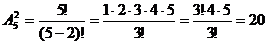
Ответ: 20.
Задание.Сколькими способами из восьми кандидатов можно выбрать три лица на три должности?
Решение. __________________________________________________________________________________________________________________________________________________________
Ответ: 336.
2. Перестановки. Перестановками из n элементов называются такие соединения из всех n элементов, которые отличаются друг от друга порядком расположения элементов.
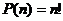(1.2)
Пример.Пусть даны три буквы А, В, С. Сколько можно составить комбинаций из этих букв?
Решение. Число перестановок из трех элементов можно вычислить по формуле: 3! =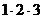 
= 6.
Ответ: 6.
Задание.Сколькими способами можно рассадить 7 человек по 7 местам?
Решение. __________________________________________________________________________________________________________________________________________________________
Ответ: 5040.
3. 
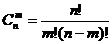Сочетания. Сочетаниями из n элементов по m в каждом называются такие соединения, которые отличаются друг от друга хотя бы одним элементом.
(1.3)
Пример.Сколькими способами можно выбрать трех дежурных, если в классе 30 учащихся?
Решение. Так как из 30 учащихся нужно выбрать 3, то можно составить комбинации, отличающиеся друг от друга хотя бы одним элементом, т.е. сочетания из 30 по 3:
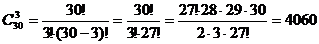
Ответ: 4060.
Задание.Сколькими способами из 15 рабочих можно создать бригады по 5 человек в каждой?
Решение.
______________________________________________________________________________________________________________________________________________________Ответ: 3003.
Вопросы для самоконтроля
1. Перечислите основные задачи комбинаторики.
2. Что называется перестановками?
3. Запишите формулу для перестановок из n элементов.
4. Что называется размещениями?
5. Запишите формулу числа размещений из n элементов по m.
6. Что называется сочетаниями?
7. Запишите формулу для числа сочетаний из n элементов по m.
Контрольное задание
- Из 6 открыток надо выбрать 3. Сколькими способами это можно сделать?
_____________________________________________________________________________
- Сколько существует вариантов распределения трех призовых мест, если в розыгрыше участвуют 7 команд?
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________
- Сколькими способами можно составить список из 20 учеников?
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________