IV. Функции нескольких переменных
1. Что называют функцией двух переменных, ее областью определения? Дайте геометрическое толкование этих понятий.
2. Дайте определение функции 3-х переменных и ее области определения.
3. Что называют пределом функции двух переменных в точке? Дайте определение функции, непрерывной в точке и в области.
4. Как определяются частные производные? Сформулируйте правило нахождения частных производных. Каков геометрический смысл частных производных функции двух переменных?
5. Какая функция  называется дифференцируемой в точке Мо(хо, уо)? Что называют полным дифференциалом функции в точке? В чем состоит правило применения полного дифференциала для вычисления приближенных значений функции?
называется дифференцируемой в точке Мо(хо, уо)? Что называют полным дифференциалом функции в точке? В чем состоит правило применения полного дифференциала для вычисления приближенных значений функции?
6. Выведите уравнение касательной плоскости и нормали к поверхности.
7. Выведите формулы для нахождения  и
и  сложной функции
сложной функции  , где
, где  .
.
8. Напишите формулу вычисления полной производной  сложной функции
сложной функции  ,
,  .
.
9. Выведите формулу дифференцирования неявной функции  , заданной уравнением
, заданной уравнением  .
.
10. Дайте определение частных производных высших порядков. Сформулируйте теорему о равенстве смешанных частных производных функции двух переменных.
11. Что называют производной функции  в данной точке М0 по направлению вектора? Выведите формулу ее вычисления.
в данной точке М0 по направлению вектора? Выведите формулу ее вычисления.
12. Что называют градиентом скалярного поля  в данной точке? Как выражается производная по направлению через градиент и единичный вектор?
в данной точке? Как выражается производная по направлению через градиент и единичный вектор?
13. Дайте определение локального максимума (минимума) функции двух переменных. Выведите необходимое условие и сформулируйте достаточное условие экстремума функции двух переменных.
14. Сформулируйте правило нахождения наибольшего и наименьшего значений функции двух переменных в замкнутой области.
15. Что называют условным экстремумом функции  ? Как найти условный экстремум, если переменные связаны одним условием?
? Как найти условный экстремум, если переменные связаны одним условием?
16. Напишите уравнение касательной и нормальной плоскости к кривой.
17. Как вычислить кривизну кривой в данной точке?
Задания для контрольной работы .
Задание 1. Найти предел функции, не пользуясь правилом Лопиталя.
1.1. а) 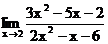 б)
б) 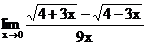
в) 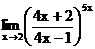 г)
г) 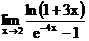
1.2. а) 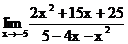 б)
б) 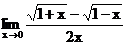
в) 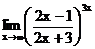 г)
г) 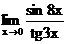
1.3. а) 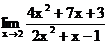 б)
б) 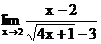
в) 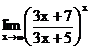 г)
г) 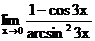
1.4. а) 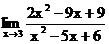 б)
б) 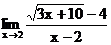
в) 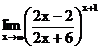 г)
г) 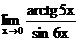
1.5. а) 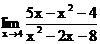 б)
б) 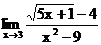
в) 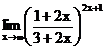 г)
г) 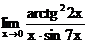
1.6. а) 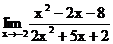 б)
б) 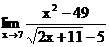
в) 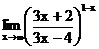 г)
г) 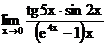
1.7. а) 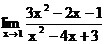 б)
б) 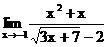
в) 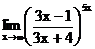 г)
г) 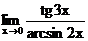
1.8. а) 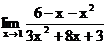 б)
б) 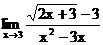
в) 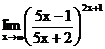 г)
г) 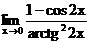
1.9. а) 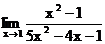 б)
б) 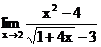
в) 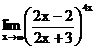 г)
г) 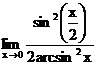
1.10. а) 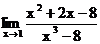 б)
б) 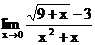
в) 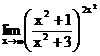 г)
г) 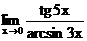
1.11. а) 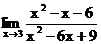 б)
б) 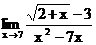
в) 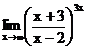 г)
г) 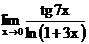
1.12. а) 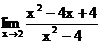 б)
б) 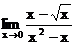
в) 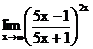 г)
г) 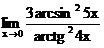
1.13. а) 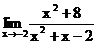 б)
б) 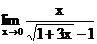
в) 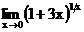 г)
г) 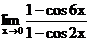
1.14. а) 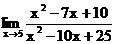 б)
б) 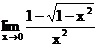
в) 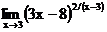 г)
г) 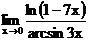
1.15. а) 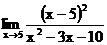 б)
б) 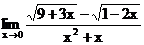
в) 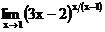 г)
г) 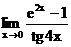
1.16. а) 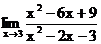 б)
б) 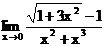
в) 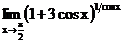 г)
г) 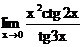
1.17. а) 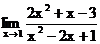 б)
б) 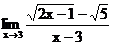
в) 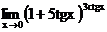 г)
г) 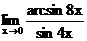
1.18. а) 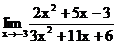 б)
б) 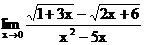
в) 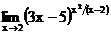 г)
г) 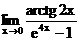
1.19. а) 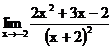 б)
б) 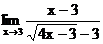
в) 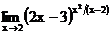 г)
г) 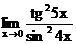
1.20. а) 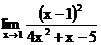 б)
б) 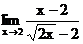
в) 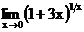 г)
г) 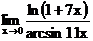
1.21 а) 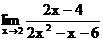 б)
б) 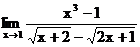
в) 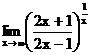 г)
г) 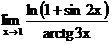
1.22 а) 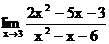 б)
б) 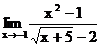
в) 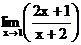 г)
г) 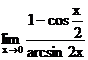
1.23 а) 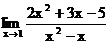 б)
б) 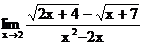
в) 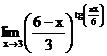 г)
г) 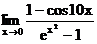
1.24 а) 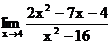 б)
б) 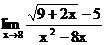
в) 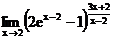 г)
г) 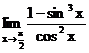 ,0
,0
Задание 2. Найти производные указанных функций.
2.1. а) 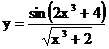 б)
б) 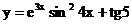 в)
в) 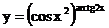
2.2. а) 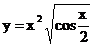 б)
б) 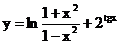 в)
в) 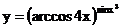
2.3. а) 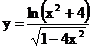 б)
б) 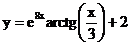 в)
в) 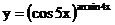
2.4. а) 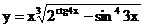 б)
б) 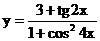 в)
в) 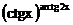
2.5. а) 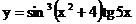 б)
б) 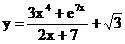 в)
в) 
2.6. а) 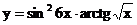 б)
б) 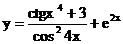 в)
в) 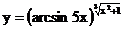
2.7. а) 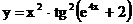 б)
б) 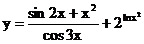 в)
в) 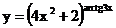
2.8. а) 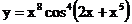 б)
б) 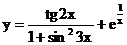 в)
в) 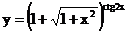
2.9. а) 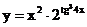 б)
б) 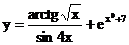 в)
в) 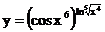
2.10. а) 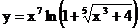 б)
б) 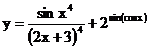 в)
в) 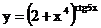
2.11. а) 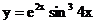 б)
б) 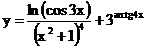 в)
в) 
2.12. а) 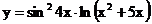 б)
б) 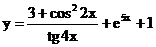 в)
в) 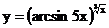
2.13. а) 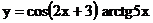 б)
б) 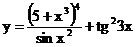 в)
в) 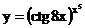
2.14. а) 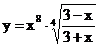 б)
б) 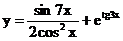 в)
в) 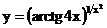
2.15 а) 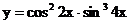 б)
б) 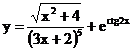 в)
в) 
2.16. а)  б)
б)  в)
в) 
2.17. а)  б)
б)  в)
в) 
2.18. а)  б)
б)  в)
в) 
2.19. а)  б)
б)  в)
в) 
2.20. а)  б)
б)  в)
в) 
2.21 а)  б)
б)  в)
в) 
2.22 а)  б)
б)  в)
в) 
2.23 а)  б)
б)  в)
в) 
2.24 а)  б)
б)  в)
в) 
Задание 3. Найти  и
и  .
.
3.1. а)  б)
б) 
3.2. а)  б)
б) 
3.3. а)  б)
б) 
3.4. а)  б)
б) 
3.5. а)  б)
б) 
3.6. а)  б)
б) 
3.7. а)  б)
б) 
3.8. а)  б)
б) 
3.9. а)  б)
б) 
3.10. а)  б)
б) 
3.11. а)  б)
б) 
3.12. а)  б)
б) 
3.13. а)  б)
б) 
3.14. а)  б)
б) 
3.15. а)  б)
б) 
3.16. а)  б)
б) 
3.17. а)  б)
б) 
3.18. а)  б)
б) 
3.19. а)  б)
б) 
3.20. а)  б)
б) 
3.21 а)  б)
б) 
3.22 а)  б)
б) 
3.23 а)  б)
б) 
3.24 а)  б)
б) 
Задание 4. Дана функция  Показать, что она является решением дифференциального уравнения.
Показать, что она является решением дифференциального уравнения.
| 4.1 |  ; ; |  |
| 4.2 |  |  |
| 4.3 |  |  |
| 4.4 |  ; ; |  |
| 4.5 |  ; ; |  |
| 4.6 |  |  |
| 4.7 |  |  |
| 4.8 |  |  |
| 4.9 |  |  |
| 4.10 |  |  |
| 4.11 |  |  |
| 4.12 |  |  |
| 4.13 |  |  |
| 4.14 |  |  |
| 4.15 |  |  |
| 4.16 |  ; ; |  |
| 4.17 |  ; ; |  |
| 4.18 |  ; ; |  |
| 4.19 |  |  |
| 4.20 |  |  |
| 4.21 |  ; ; |  |
| 4.22 |  ; ; |  |
| 4.23 |  ; ; |  |
| 4.24 |  |  |
Задание 5. Найти производные указанного порядка функции, заданной неявно 
| 5.1 |  |  |
| 5.2 |  |  |
| 5.3 |  |  |
| 5.4 |  ; ; |  |
| 5.5 |  |  |
| 5.6 |  ; ; |  |
| 5.7 |  |  |
| 5.8 |  |  |
| 5.9 |  |  |
| 5.10 |  |  |
| 5.11 |  ; ; |  |
| 5.12 |  ; ; |  |
| 5.13 |  ; ; |  |
| 5.14 |  ; ; |  |
| 5.15 |  ; ; |  |
| 5.16 |  ; ; |  |
| 5.17 |  ; ; |  |
| 5.18 |  ; ; |  |
| 5.19 |  ; ; |  |
| 5.20 |  ; ; |  |
| 5.21 |  |  |
| 5.22 |  |  |
| 5.23 |  |  |
| 5.24 |  |  |
ЛИТЕРАТУРА:
1. Зимина О.В. Линейная алгебра и аналитическая геометрия: Учебное пособие для студентов вузов. – М.: Издательство МЭИ, 2000.
2. Шипачев В.С. Высшая математика: Учебник для вузов. – 5-е издание. – М.: Высшая школа, 2002.
* ) – укажите свойства определяемого понятия
