Задачи экономического анализа, решаемые на основе регрессионных эконометрических моделей

7.1. Измерение тесноты связи между результативным и факторными признаками 135

7.2. Анализ влияния отдельных факторных признаков на результативный признак 145

7.3. ПРАКТИЧЕСКИЙ БЛОК 148

7.4. САМОСТОЯТЕЛЬНАЯ РАБОТА СТУДЕНТОВ 166

7.1. Измерение тесноты связи между результативным и факторными признаками.

7.1.1. Линейная корреляция.

1. Простая линейная корреляция при несгруппированных данных.

Если между двумя явлениями х и у существует линейное стохастическое соотношение – линейная регрессия, то степень интенсивности связи можно измерить с помощью коэффициента корреляции r_xy. Корреляция в широком смысле слова означает связь, соотношение между объективно существующими явлениями и процессами. Соотношение между регрессией и корреляцией можно представить в виде следующей схемы, предложенной Браве и Пирсоном.

Пусть заданы значения переменных х и у, между которыми существует линейное соотношение.

у, х – средние значения переменных или их математические ожидания;

n – число проведенных наблюдений;

σ_х– стандартное отклонение х;

σ_у – стандартное отклонение у.

Представим уравнение

в эквивалентном виде

В этой системе величина

показывает, на сколько величин σ_у изменится в среднем у, когда х увеличится на одно σ_х.

Величина r является показателем тесноты связи и называется выборочным коэффициентом корреляции или простым линейным коэффициентом корреляции или парным коэффициентом или просто коэффициентом корреляции.

Отметим другие модификации формулы для r.

В данной формуле σ_х и σ_у – выборочные средние квадратические отклонения для переменных х и у, а σ_ху– выборочный корреляционный момент или выборочная ковариация.

Определение. Ковариацией случайных величин х и у называется математическое ожидание произведения отклонений этих величин от своих математических ожиданий, т.е.

Ковариация двух случайных величин характеризует как степень связи случайных величин, так и их рассеяние вокруг точки (х, у). Ковариация – величина размерная, что затрудняет ее использование для оценки степени зависимости случайных величин. Коэффициент корреляции лишен этих недостатков.

Для практических расчетов наиболее удобна следующая формула

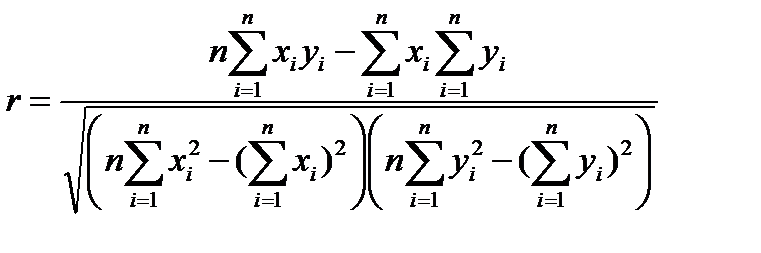
По ней коэффициент корреляции находится непосредственно из данных наблюдений и на его значении не скажутся округления данных, связанные с расчетом средних и отклонений от них.

Коэффициент корреляции обладает следующими свойствами:

– Принимает значения на отрезке от –1 до 1, т.е. -1≤r≤ 1. Чем ближе | r_ух | к 1, тем теснее связь.

– При r_ух = ±1 корреляционная связь представляет собой линейную функциональную зависимость. При этом все наблюдаемые значения располагаются на прямой линии. При r = 1 между отклонениями х_i – х и у_i – усуществует прямая связь, а при r= -1 обратная.

– r = 0 показывает на отсутствие линейной связи между переменными, а не на отсутствие связи вообще. При этом линия регрессии параллельна оси «Ох».

– При вычислении коэффициента корреляции для линейной регрессии безразлично, какая переменная является зависимой, а какая объясняющей, т.е. r_ух = r_ху.

Коэффициент корреляции не изменится, если переменные подвергнуть преобразованию или изменить их единицы измерения.

2. Простая линейная корреляция при сгруппированных данных.

Отклонения х_j – х взвешиваем по частотам g_ij-го интервала значений объясняющей переменной х, отклонения у_k – у – по частотам h_kk-го интервала зависимой переменной у, а произведение отклонений (х_j – х)(у_к – у) – по условным частотам p_kj.

Поэтому

Коэффициент корреляции, вычисленный по несгруппированному материалу более точен, чем коэффициент корреляции вычисленный по сгруппированным данным, так как свободен от погрешности вносимой группировкой данных.

3. Связь между коэффициентами корреляции, регрессии и детерминации.

Коэффициент а₁ простой линейной регрессии y = а₀ + а₁x переменной у на х определяется отношением

Коэффициент корреляции определяется следующим соотношением:

Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции, называемый коэффициентом детерминации. Коэффициент детерминации для простой линейной регрессии (парной детерминации) определяется следующим соотношением:

Это отношение показывает, какая часть общего рассеяния значений у обусловлена изменчивостью переменной х. Это соотношение можно преобразовать:

Если коэффициент детерминации равен 1, то все эмпирические данные лежат на корреляционной прямой, а если он равен 0, то ни о какой численной линейной зависимости переменной у от х в статистическом понимании не может быть и речи. Коэффициент детерминации – безразмерная величина, не реагирующая на преобразования переменных.

С коэффициентом детерминации связано понятие меры неопределенности регрессии:

Рассмотрим теперь сопряженную регрессию:

Тогда

и поэтому

4. Линейная множественная корреляция. Частная корреляция.

Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком, или, иначе, оценивает тесноту совместного влияния факторов на результат. Независимо от формы связи показатель множественной корреляции может быть найден по формуле как индекс множественной корреляции

где σ_у²– общая дисперсия результативного признака,

Значение индекса множественной корреляции лежит в пределах от 0 до 1 и должно быть больше или равно максимальному парному индексу корреляции:

= 1, 2, …m

При линейной зависимости признаков формула индекса корреляции может быть представлена и через стандартизированные коэффициенты регрессии следующим образом:

r_ухi – парные коэффициенты корреляции результата с каждым фактором.

Формула индекса множественной корреляции для линейной регрессии получила название линейного коэффициента множественной корреляции, или, совокупного коэффициента корреляции.

При линейной зависимости возможно так же определение совокупного коэффициента корреляции через матрицу парных коэффициентов корреляции

Эта формула позволяет определять совокупный коэффициент корреляции, не обращаясь при этом к уравнению множественной регрессии, а используя лишь парные коэффициенты корреляции.

Частные коэффициенты (или индексы) корреляции, измеряющие влияние науфактора х_iпри неизменном уровне других факторов, можно определить по формуле

или по рекуррентной формуле

Частные коэффициенты корреляции изменяются в пределах от –1 до 1. Качество построенной модели в целом оценивает коэффициент (индекс) детерминации. Он рассчитывается как квадрат индекса множественной корреляции: R²_yx1…xm.

5. Влияние неучтенных факторов на коэффициент корреляции.

На коэффициент корреляции при экономических расчетах могут оказывать влияние следующие факторы:

- географический фактор: природно-климатические и физико-географические условия;

- фактор времени: следует учитывать, за какой период по экономическим данным вычисляется коэффициент корреляции – за месяц, квартал, год;

- однородность группировки социально-экономических явлений по комплексу признаков. Исследователь должен располагать теоретически обоснованным критерием определения статистической однородности.

7.1.2. Нелинейная корреляция.

1. Нелинейная корреляция для парного уравнения регрессии.

Уравнение нелинейной регрессии, как и в линейной зависимости, дополняется показателем корреляции, а именно индексом корреляции:

где Так как

то индекс корреляции можно выразить как

Величина данного показателя находится в границах: 0≤R≤1, чем ближе к единице, тем теснее связь рассматриваемых признаков, тем более надежно найденное уравнение регрессии.

Если нелинейное относительно объясняемой переменной уравнение регрессии при линеаризации принимает форму линейного уравнения парной регрессии, то для оценки тесноты связи может быть использован линейный коэффициент корреляции, величина которого в этом случае совпадает с индексом корреляции R_ху= r_уz, где z – преобразованная величина признака-фактора, например, z = 1/x или z = lnx.

Обратимся для примера к равносторонней гиперболе y = b + a/x. Заменив 1/x на z, имеем линейное уравнение y = b + az, для которого может быть определен линейный коэффициент корреляции: r=a×s_z/s_y . Возводя данное выражение в квадрат, получим:

Преобразовывая далее, придем к следующему выражению для

следовательно,

Но так как

и , то

Таким образом, приходим к формуле индекса корреляции

Заменив далее zна 1/х, получим , соответственно . Аналогично для других функций подобного вида, в которых образования в линейный вид не затрагивают зависимую переменную, и требование МНК выполнимо.

Иначе обстоит дело, когда преобразования уравнения в линейную форму связаны с зависимой переменной. В этом случае линейный коэффициент корреляции по преобразованным значениям признаков дает лишь приближенную оценку тесноты связи и численно не совпадает с индексом корреляции.

Например, при степенной функции после перехода к логарифмически линейному уравнению может быть найден линейный коэффициент корреляции не для фактических значений х и у, а для их логарифмов, то есть . Соответственно квадрат его значения будет характеризовать отношение факторной суммы квадратов отклонений к общей, но не для у, а для его логарифмов:

Между тем при расчете индекса корреляции используются суммы квадратов отклонений признака у, а не их логарифмов. С этой целью определяются теоретические значения результативного признака, то есть у, как антилогарифм рассчитанной по уравнению величины lny и остаточная сумма квадратов как . Индекс корреляции определяется по формуле

В знаменателе расчета участвует сумма квадратов отклонений фактических значений уот их средней величины, а в расчете участвует . Соответственно различаются числители рассматриваемых показателей:

– в индексе корреляции и – в коэффициенте корреляции.

Необходимо также помнить, что если при линейной зависимости признаков сопряженные регрессии имеют один и тот же коэффициент корреляции, то есть , то при криволинейной зависимости они не равны, то есть .

Так как в расчете индекса корреляции используется соотношение факторной и общей суммы квадратов отклонений, то R² имеет тот же смысл, что и коэффициент детерминации. В специальных исследованиях величину R² для нелинейных связей называют индексом детерминации.

Оценка существенности индекса корреляции проводится, так же как и оценка надежности коэффициента корреляции. Индекс детерминации используется для проверки существенности в целом уравнения линейной регрессии по F –критерию Фишера:

,

где n– число наблюдений, m – число параметров при переменной х. Величина m характеризует число степеней свободы для факторной суммы квадратов, а (n-m-1) – число степеней свободы для остаточной суммы квадратов.

Индекс детерминации можно сравнивать с коэффициентом детерминации для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем величина коэффициента детерминации меньше индекса детерминации . Близость иx означает, что нет необходимости усложнять форму уравнения регрессии и можно использовать линейную функцию. Если , то предположение о линейной форме связи считается оправданным. В противном случае проводится оценка существенности различия и , вычисленных по одним и тем же исходным данным через t-критерий Стьюдента:

, где – ошибка разности между и .

Если t_ф >t_т, то различия между рассматриваемыми показателями корреляции существенны и замена нелинейной регрессии уравнением линейной функции невозможна. Если t< 2, то различия несущественны и, следовательно, возможно применение линейной регрессии.

2. Нелинейная корреляция для множественного уравнения регрессии.

Для криволинейной зависимости, нелинейной по переменным, индекс множественной корреляции равен совокупному коэффициенту корреляции.

Например, пусть для фирмы модель прибыли у имеет вид

у = a₀ + а₁x₁ + а₂x₂ + а₃lnx₃+ а₄lnx_{4 ,}

где х₁ – удельные расходы на рекламу;

х₂ – капитал фирмы;

х₃ – доля продукции фирмы в общем объеме продаж данной группы товаров по региону;

х₄ – процент увеличения объема продаж фирмы по сравнению с предыдущим годом.

Тогда независимо от того, что фактор х₁ задан линейно, а х₂, х₃, х₄ – в логарифмах, оценка тесноты связи может быть произведена с помощью линейного коэффициента множественной корреляции.

Иначе обстоит дело с криволинейной регрессией, нелинейной по оцениваемым параметрам. Предположим, что рассматривается производственная функция Кобба-Дугласа:

, где P– объем продукции, L – затраты труда, К – величина капитала, b₁+b₂=1.

Логарифмируя ее, получим линейное уравнение в логарифмах

LnP = lna + b₁lnL + b₂lnK

Индекс детерминации для нелинейных по оцениваемым параметрам функции принять называть «квазиR²» определения по функциям, использующим логарифмические преобразования (степенная, экспонента), необходимо найти сначала теоретические значения lny, затем трансформировать их через антилогарифмы, то есть найти теоретические значения результативного признака и далее определять индекс детерминации как «квазиR²» по формуле

Величина индекса множественной корреляции, определенная как «квазиR²» не будет совпадать с совокупным коэффициентом корреляции.

Для того чтобы не допустить возможного преувеличения тесноты связи, используется скорректированный индекс (коэффициент) множественной корреляции. Он содержит поправку на число степеней свободы и рассчитывается по формуле

, где n – число наблюдений, m – число факторов.

Чем больше величина m, тем сильнее различия между .

Для линейной зависимость признаков скорректированный коэффициент корреляции определяется по той же формуле, что и индекс множественной корреляции. Отличие заключается лишь в том, что в линейной зависимости под m понимается число факторов, включенных в анализ, а в криволинейной зависимости это число параметров при х. Например, если y=f(x₁,x₂), то для линейной зависимости m = 2, а для регрессии вида

у = a₀ + а₁x₁²+а₁₂x₁ + а₂x₂ +а₂₂x₂²

число параметров при х равно 4, то есть m = 4.