Числовые характеристики выборочного распределения

Рассмотрим выборку 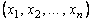как генеральную совокупность 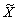дискретного типа со значениями 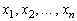, которые 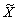принимает с равными вероятностями , .

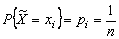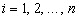По определению начальные моменты 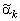и центральные моменты 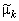такой генеральной совокупности равны, соответственно,

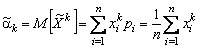
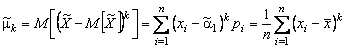, где .

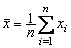Эти числовые характеристики называются выборочными характеристиками.

Выборочную характеристику

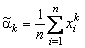(4.2.6)

называют выборочным начальным моментом 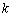-го порядка. В частности, момент

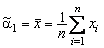(4.2.7)

называется выборочным средним.

Выборочная характеристика

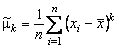(4.2.8)

называется выборочным центральным моментом 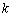-го порядка. В частности, при 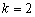получаем выборочную дисперсию

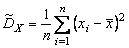. (4.2.10)

Замечание

При большом объёме выборки ( 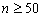) перечисленные характеристики обычно находят по группированным данным (и 4.2.2). Так, если 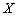- генеральная совокупность дискретного типа, то вместо формул (4.2.6) - (4.2.10) для подсчёта выборочных моментов 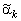и 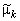используют равенства

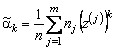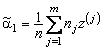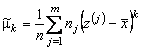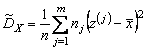, , , , см. табл. 4.2.1.

Если же генеральная совокупность 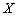относится к непрерывному типу, то соответствующие равенства выглядят так:

, , , ,

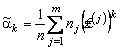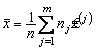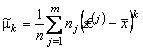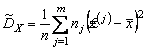где 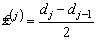- середины промежутков разбиения, см табл. 4.2.2

Аналогично вводятся выборочные характеристики многомерных генеральных совокупностей (случайных векторов). Например, пусть 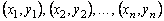- выборка объёма 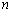из двумерной генеральной совокупности 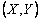. Выборочную характеристику

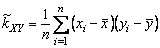(4.2.11)

называют выборочной ковариацией, а характеристику

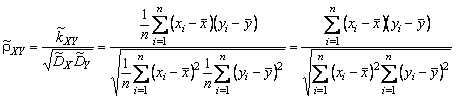(4.2.12)

- выборочным коэффициентом корреляции.

Рассмотрим формулы, упрощающие вычисление выборочных характеристик (4.2.10) – (4.2.12).

Пример 4.2.2.

Покажем, что

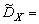
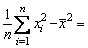
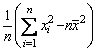. (4.2.13)

◄ .

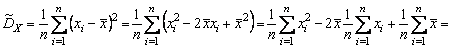
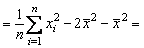
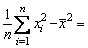
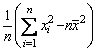Заметим, что равенство 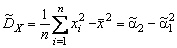для выборочных моментов является аналогом соответствующей формулы для теоретических (обычных) моментов: .►

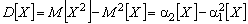Упражнения

4.2.3. Покажите, что

.

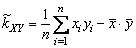4.2.4. Убедитесь в том, что выборочные характеристик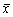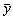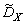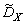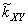и , , , , и 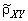двумерной генеральной совокупности 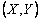можно вычислять по выборке 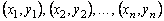в следующей последовательности:

а) подсчитать суммы 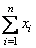, , 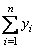, 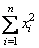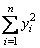и ;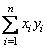

б) затем вычислить

,

,

;

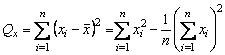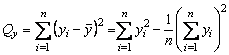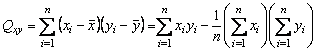в) окончательно найти

, ;

, , , .

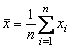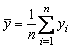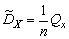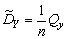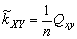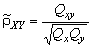Список рекомендуемой литературы

1. Баврин, И. И. Высшая математика: учебник по естественно–научным направлениям и специальностям / И. И. Баврин. – Москва: Академия, 2016. – 611 с.

2. Выгодский, М. Я. Справочник по высшей математике / М. Я. Выгодский. – Москва: АСТ: Астрель, 2017. – 703 с.

3. Высшая математика / А. И. Астровский, Е. В. Воронкова, О. П. Степанович: учебно-методический комплекс. – Минск: Издательство МИУ, 2015. – 383 с.

4. Высшая математика: учебник / К. В. Балдин, В. Н. Башлыков, А. В. Рукосуев. – Москва: Флинта: МПСИ, 2016. – 359 с.

5. Высшая математика для экономистов: курс лекций / П. С. Геворкян [и др.]. – Москва: Эконом, 2015. – 351 с.

6. Высшая математика: курс лекций: для студентов экономических специальностей / Г. М. Булдык. – Минск: ФУАинформ, 2016. – 541 с.

7. Краткий курс высшей математики: учебник / К. В. Балдин [и др.]. – Москва: Дашков и Кº, 2017. – 510 с.

8. Кундышева, Е. С. Математика: учебник / Е. С. Кундышева. – Москва: Дашков и Кº, 2016. – 561 с.

9. Малыхин, В. И. Высшая математика: учебное пособие / В. И. Малыхин. – Москва: Инфра-М, 2016. – 363 с.