Определение первообразной и неопределенного интеграла
Функция F(x) называется первообразной функции f(x), если
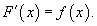
Множество всех первообразных некоторой функции f(x) называется неопределенным интегралом функцииf(x) и обозначается как
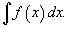
Таким образом, если F - некоторая частная первообразная, то справедливо выражение
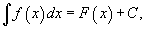
где С - произвольная постоянная.
Свойства неопределенного интеграла
В приведенных ниже формулах f и g - функции переменной x, F - первообразная функции f,
а, k, C - постоянные величины.
· 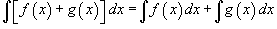
· 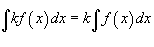
· 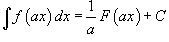
· 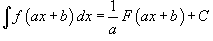
Таблица интегралов
В формулах ниже предполагается, что a, p (p ≠ 1), C - действительные постоянные, b - основание показательной функции (b ≠ 1, b > 0).
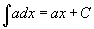 | 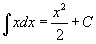 |
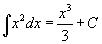 | 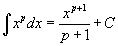 |
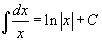 | 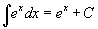 |
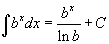 | 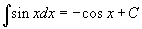 |
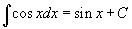 | 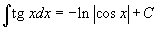 |
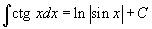 | 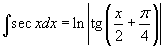 |
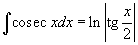 | 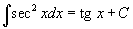 |
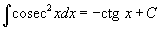 | 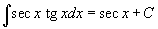 |
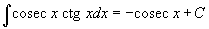 | 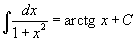 |
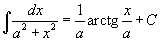 | 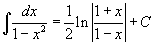 |
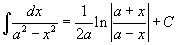 | 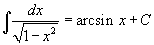 |
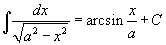 | 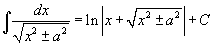 |
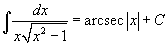 | 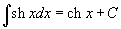 |
Определенный интеграл.
Формула Ньютона – Лейбница.
Пусть функция f (x) непрерывна на замкнутом интервале [a, b]. Определенный интеграл от функции f (x) в пределах от a до b вводится как предел суммы бесконечно большого числа слагаемых, каждое из которых стремится к нулю: 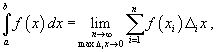 где где 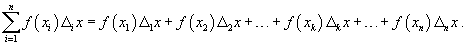 Свойства определенного интеграла Ниже предполагается, что f (x) и g (x) - непрерывные функции на замкнутом интервале [a, b]. 1. Свойства определенного интеграла Ниже предполагается, что f (x) и g (x) - непрерывные функции на замкнутом интервале [a, b]. 1. 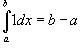 2. 2. 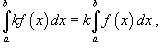 где k - константа; 3. где k - константа; 3. 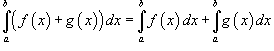 4. 4. 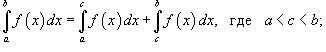 |
Дифференциальные уравнения (д.у.)
О: Дифференциальным уравнением называется уравнение, содержащее производные искомой функции
или ее дифференциалы.
0: Порядком дифференциального уравнения называется наивысший порядок дифференциала или
производной от искомой функции в составе данного уравнения.
Дифференциальные уравнения 1-го порядка
О: Д,у.вида f(x)dx=g(y)dyназывается д.у. с разделенными переменными.
О: Д.у.вида f(x)F(y)dx+g(x)G(y)dy=0,называется д.у. с разделяющимися переменными, где f(x), F(y),
g(x), б(у) — заданные функции
О: Решение, содержащее производную постоянную С, называется общим решением д.у.
Алгоритм решения дифференциального уравнения:
1) Представить у' 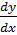 как отношение дифференциалов;
как отношение дифференциалов;
2) Если необходимо, разделить слагаемые таким образом, чтобы дифференциалы dy и dx были в разно частях уравнения.
3) Необходимо преобразовать дифференциальное уравнение таким образом, чтобы все переменные, зависящие от х были в одной части уравнения, а переменные, зависящие от у были в другой части уравнения. Т.е. привести к виду f(x)dx=g(y)dy.
4) Вычислить интеграл от обеих частей уравнения. Получим общее решение.
5) Если заданы начальные условия, то подставив их в общее решение, найдем постоянную С. Зная С, подставим его в общее решение, получим частное решение.
Теория вероятности
0: Испытанием называется всякое действие, явление, наблюдение с несколькими различными
исходами, реализуемое при данном комплексе условий.
0: Результат испытания называется событием.
Виды событий:
| Достоверными | называют события, которые обязательно произойдут при данных условиях. |
| Невозможными | называют события, которые не могут произойти при данных условиях. |
| Равновозможными | называют события, возможности наступления которых одинаковы, |
| Несовместными | называют события, если никакие два из них не могут произойти в данном опыте вместе. |
| Совместными | называют события, если они могут произойти в данном опыте вместе. |
| Противоположными | называют события А и А, такие, что если не происходит одно А, то другое А обязательно произойдет. |
| Независимыми | называют события, если возможность наступления одного из них не влияет на возможность наступления другого. |
| Зависимыми | называют события, если возможность наступления одного из них влияет на возможность наступления другого. |
Пример 1: Подбрасывание монеты — это испытание, а выпадение орла или решки — событие. При
подбрасывание монеты, события, заключающиеся в выпадение орла или решки будут
равновозможными и будут несовместными, т.к. не может одновременно выпасть орел и решка.
Пример 2: Бросая игральную кость, рассмотрим два события: А — выпадение чисел 1, 2, 3,
В — выпадение четного числа очков. События А и В совместны, т.к. у них есть общее значение-
выпадение числа 2.
Операции над событиями:
1) Суммой событий А и В называется событие, состоящее в наступлении хотя бы одного из них. А+В
2) Произведением двух событий А и В называется событие, состоящее в том, что каждое из них
произойдет. А В.
Классическое определение вероятности:
0: Вероятность события А равна отношению числа ш исходов испытаний, благоприятствующих наступлению события А, к общему числу п всех равновозможных несовместных исходов.
Р(А)=и
Свойства вероятности
1) А — любое событие, О < Р(А) « 1;
2) А — достоверное событие, Р(А)=1;
3) А — невозможное событие, Р(А)=0.
Пример 3: При бросании игральной кости возможно 6равновозможных исходов — выпадение чисел 1,;
3, 4, 5, 6. Пусть событие А — выпадение четного числа очков А=(2, 4, 6). Всего 6 исходов,
3 1 интересующих нас исходов 3 варианта. Вероятность выпадения четного числа очков P(A) = — =—
6 2
Теоремы сложения и умножения вероятностей:
Теорема 1: Если А и В несовместные события, то сумма вероятностей этих событий Р(А+В)=Р(А)+Р(В' Пример: При бросании игральной кости, событие А — впадение числа 1, событие В — выпадение четного числа очков. А=(1), В=~2, 4, 6), P(A)=1/6, Р(В)=3/6=1/2.
А+В=~1, 2, 4, 6), P(A+B)=1/6+ 3/6 = 4/6=2/3.
Теорема 2: Если А и В совместные события, то сумма вероятностей этих событий Р(А+В)=Р(А)+Р(В)Р(А В).
Пример: При бросании игральной кости, событие А — впадение числа 2, событие В — выпадение четного числа очков. А=(2), В=(2, 4, 6), А В=(2), P(AB)=1/6.
Теорема 3: Если А и В несовместные события, то одновременное появление этих событий равно Р(А В)=Р(А) Р(В).
Теорема 4: Вероятность противоположного события Р(А)= 1-Р(А).
Для решения задач на вычисление вероятности вам необходимо посчитать сколько всего возможно вариантов исхода данного события и сколько вариантов удовлетворяет данному событию.
Математическая статистика
Математическая статистика – это наука, изучающая случайные явления посредством обработки и анализа результатов наблюдений и измерений.
Первая задача математической статистики – указать способы получения, группировки и обработки статистических данных, собранных в результате наблюдений, специально поставленных опытов или произведённых измерений.
Вторая задача математической статистики – разработка методов анализа статистических сведений в зависимости от целей исследования. Например, целью исследования может быть:
- оценка неизвестной вероятности события;
- оценка параметров распределения случайной величины;
- оценка неизвестной функции распределения случайной величины;
- проверка гипотез о параметрах распределения или о виде неизвестного распределения;
- оценка зависимости случайной величины от одной или нескольких случайных величин и т.д.
Случайную величину 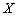 будем называть генеральной совокупностью
будем называть генеральной совокупностью 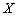 .
.
Исходным материалом для изучения свойств генеральной совокупности 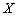 являются статистические данные, т.е. значения
являются статистические данные, т.е. значения 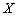 , полученные в результате повторения случайного опыта (измерения случайной величины
, полученные в результате повторения случайного опыта (измерения случайной величины 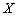 ). Предполагается, что опыт может быть повторён сколько угодно раз в неизменных условиях. Это означает, что распределение случайной величины
). Предполагается, что опыт может быть повторён сколько угодно раз в неизменных условиях. Это означает, что распределение случайной величины 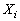 ,
, 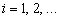 , заданной на множестве исходов
, заданной на множестве исходов 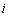 -го опыта, не зависит от
-го опыта, не зависит от 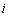 и совпадает с распределением генеральной совокупности
и совпадает с распределением генеральной совокупности 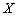 .
.
Набор 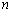 независимых в совокупности случайных величин
независимых в совокупности случайных величин 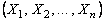 , где
, где 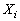 соответствует
соответствует 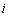 -му опыту, называют случайной выборкой из генеральной совокупности
-му опыту, называют случайной выборкой из генеральной совокупности 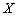 . Число
. Число 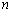 называетсяобъёмом выборки.
называетсяобъёмом выборки.
Совокупность чисел 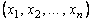 , полученных в результате
, полученных в результате 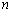 -кратного повторения опыта по измерению генеральной совокупности
-кратного повторения опыта по измерению генеральной совокупности 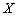 , называется реализацией случайной выборки или простовыборкой объёма
, называется реализацией случайной выборки или простовыборкой объёма 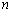 .
.
В основе большинства результатов математической статистики лежит выборочный метод, состоящий в том, что свойства генеральной совокупности 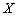 устанавливаются путём изучения тех же свойств на случайной выборке.
устанавливаются путём изучения тех же свойств на случайной выборке.
Предварительная обработка выборки
Прежде, чем перейти к детальному анализу статистических данных, обычно проводят их предварительную обработку. Иногда её результаты уже сами по себе дают ответы на многие вопросы, но в большинстве случаев они являются исходным материалом для дальнейшего анализа.
Вариационный ряд
Простейшее преобразование статистических данных является их упорядочивание по величине.
Выборка 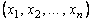 объёма
объёма 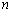 из генеральной совокупности
из генеральной совокупности 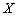 , упорядоченная в порядке неубывания элементов, т.е.
, упорядоченная в порядке неубывания элементов, т.е. 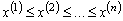 , называется вариационным рядом:
, называется вариационным рядом:
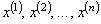 .
.
Разность между максимальным и минимальным элементами выборки 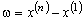 называют размахом выборки.
называют размахом выборки.
Статистический ряд
Пусть выборка 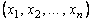 содержит
содержит 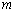 различных чисел
различных чисел 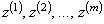 , где
, где 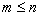 и
и 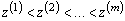 , причём число
, причём число 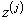 встречается в выборке
встречается в выборке 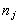 раз,
раз, 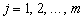 . Так бывает либо тогда, когда генеральная совокупность
. Так бывает либо тогда, когда генеральная совокупность 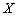 - дискретная случайная величина, либо когда
- дискретная случайная величина, либо когда 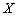 - непрерывна, но её значения при измерении округляют.
- непрерывна, но её значения при измерении округляют.
Число 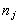 называют частотой элемента выборки
называют частотой элемента выборки 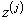 , а отношение
, а отношение 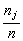 - относительной частотой этого элемента.
- относительной частотой этого элемента.
Статистическим рядом для данной выборки 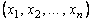 называют таблицу, которая в первой строке содержит значения выборки
называют таблицу, которая в первой строке содержит значения выборки 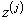 (напомним:
(напомним: 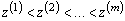 ), во второй строке – частоты
), во второй строке – частоты 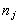 , а в третьей строке – относительные частоты
, а в третьей строке – относительные частоты 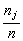 этих значений:
этих значений:
Таблица 4.2.1
Значения 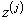 | 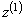 | 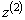 | … | 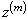 |
Частоты 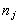 | 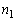 | 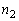 | … | 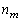 |
Относительные частоты 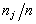 | 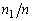 | 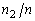 | … | 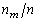 |
Статистические данные, представленные в виде статистического ряда, называют группированными.
Другой способ группировки, который используют обычно при больших объёмах выборки ( 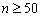 ) состоит в следующем. Отрезок
) состоит в следующем. Отрезок 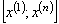 , содержащий выборку
, содержащий выборку 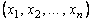 , разбивают на
, разбивают на 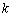 промежутков
промежутков 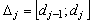 , как правило, одинаковой длины
, как правило, одинаковой длины 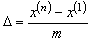 . Далее, подсчитывают частоты
. Далее, подсчитывают частоты 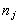 попадания выборочных значений
попадания выборочных значений 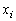 в промежутки
в промежутки 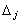 и относительные частоты
и относительные частоты 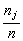 . Получающийся в результате этого статистический ряд
. Получающийся в результате этого статистический ряд
Таблица 4.2.2
Промежутки 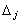 | 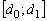 | 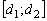 | … | 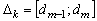 |
Частоты 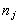 | 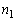 | 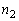 | … | 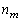 |
Относительные частоты 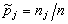 | 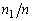 | 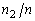 | … | 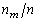 |
называют интервальным статистическим рядом.
Замечания
1. Может оказаться, что часть значений выборки 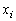 совпадают с некоторыми границами
совпадают с некоторыми границами 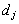 между соседними промежутками
между соседними промежутками 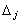 и
и 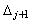 . Тогда при подсчёте частот
. Тогда при подсчёте частот 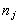 и
и 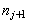 такие значения
такие значения 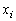 учитывают одним из следующих способов:
учитывают одним из следующих способов:
а) считают, что 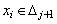 , т.е. каждое выборочное значение
, т.е. каждое выборочное значение 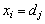 увеличивает частоту
увеличивает частоту 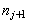 на единицу и не влияет на частоту
на единицу и не влияет на частоту 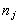 ;
;
б) каждое значение выборки 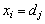 «делится между промежутками
«делится между промежутками 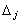 и
и 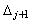 поровну», т.е. и
поровну», т.е. и 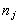 , и
, и 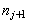 увеличиваются за счёт этого значения на
увеличиваются за счёт этого значения на 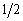 . При таком подсчёте частоты
. При таком подсчёте частоты 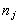 могут оказаться полуцелыми, например,
могут оказаться полуцелыми, например, 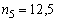 .
.
2. Число 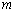 промежутков, на которые разбивают отрезок
промежутков, на которые разбивают отрезок 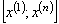 , выбирают в зависимости от объёма выборки
, выбирают в зависимости от объёма выборки 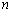 . Существуют различные критерии выбора
. Существуют различные критерии выбора 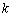 , например, ориентировочную оценку числа промежутков можно получить из соотношения
, например, ориентировочную оценку числа промежутков можно получить из соотношения 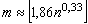 , где
, где  - целая часть
- целая часть 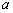 .
.
3. В некоторых источниках в качестве статистического ряда рассматривается таблица, содержащая либо только частоты 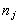 , либо только относительные частоты
, либо только относительные частоты 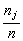 .
.
