Изображение комплексных чисел. Модуль и аргумент комплексного числа

Рассмотрим на плоскости декартову прямоугольную систему координат 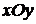. Каждому комплексному числу 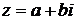можно сопоставить точку с координатами 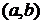, и наоборот, каждой точке с координатами 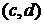можно сопоставить комплексное число 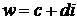. Таким образом, между точками плоскости и множеством комплексных чисел устанавливается взаимно однозначное соответствие. Поэтому комплексные числа можно изображать как точки плоскости. Плоскость, на которой изображают комплексные числа, обычно называют комплексной плоскостью.

Пример.Изобразим на комплексной плоскости числа :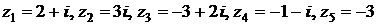

Рис. 9. Изображение комплексных чисел точками плоскости

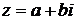Однако чаще комплексные числа изображают в виде вектора с началом в точке , а именно, комплексное число изображается радиус-вектором точки с координатами . В этом случае изображение комплексных чисел из предыдущего примера будет таким:

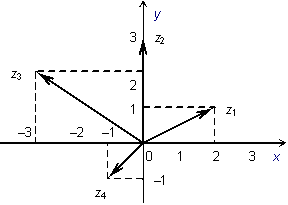
Рис. 10. Изображение комплексных чисел векторами

Отметим, что изображением суммы двух комплексных чисел является вектор, равный сумме векторов, изображающих числа и . Иными словами, при сложении комплексных чисел складываются и векторы, их изображающие (рис. 11).

Рис. 11. Изображение суммы комплексных чисел

Пусть комплексное число 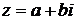изображается радиус-вектором. Тогда длина этого вектора называется модулем числа 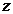и обозначается 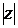. Из рисунка 12 очевидно, что .

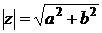Рис. 12.Модуль и аргумент

Угол, образованный радиус-вектором числа 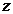с осью 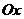, называется аргументом числа 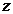и обозначается 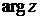. Аргумент числа определяется не однозначно, а с точностью до числа, кратного 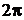. Однако, обычно аргумент указывают в диапазоне от 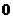до 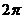или в диапазоне от 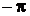до 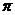. Кроме того у числа 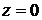аргумент не определен.

На рис. 9 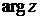равен углу 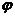. Из того же рисунка очевидно, что .

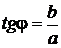С помощью этого соотношения можно находить аргумент комплексного числа:

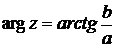или ,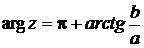

причем первая формула действует, если изображение числа 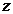находится в первой или четвертой четверти, а вторая, если - во второй или третьей. Если 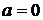, то комплексное число изображается вектором на оси 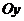и его аргумент равен или .

Тригонометрическая форма комплексного числа

Пусть 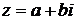. Положим 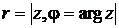. Из рисунка 9 очевидно, что .

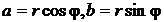Тогда 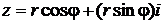. Это выражение запишем в виде

.

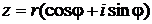Последняя запись называется тригонометрической формой комплексного числа. В отличие от нее запись числа в виде 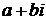называют иногда алгебраической формой комплексного числа.

Пример.Запишите в тригонометрической форме числа .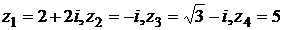

Решение. Находим модуль, аргумент, а затем выписываем тригонометрическую форму:

.

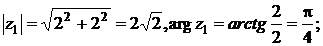
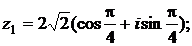
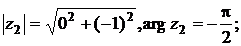
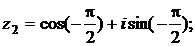
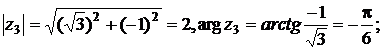
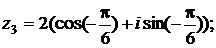
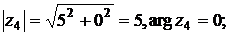
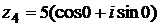Для возведения комплексного числа 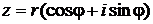в степень 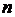, где - натуральное число применяется формула Муавра

.

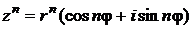Пример.Вычислите 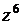, если .

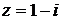Решение. Находим тригонометрическую форму числа :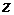

, .

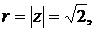
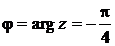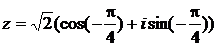По формуле Муавра

.

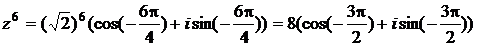Переходим к алгебраической форме, вычисляя косинус и синус: .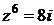

Ответ. 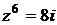.