Определители второго и третьего порядков

Определители определены только для квадратных матриц.

Определителем второго порядка называется число, которое вычисляется по формуле: .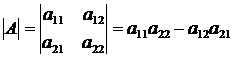

Пример. Вычислить определитель матрицы .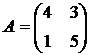

Решение. .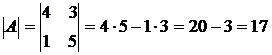

Ответ: .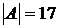

Определителем третьего порядка называется число, которое вычисляется по формуле:

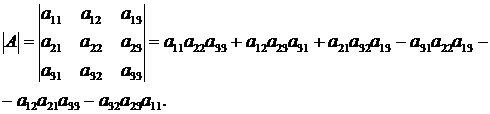
Запомнить эту формулу помогает схема, которая называется «правилом треугольника»:

Эти 3 слагаемых берутся Эти 3 слагаемых берутся

со знаком «+» со знаком «–»

Пример. Вычислить определитель третьего порядка

.

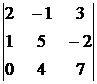Решение. Используя приведенные выше схемы, получим

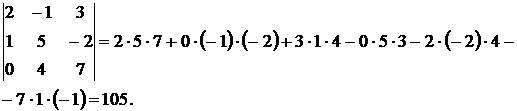
Ответ: 105.

Минором 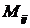элемента 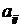определителя 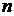-го порядка называется определитель 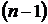-го порядка, который получается в результате вычеркивания в определителе n-го порядка строки и столбца, содержащих элемент .

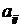Алгебраическим дополнением 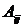элемента 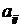называется его минор, умноженный на :

.

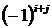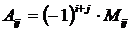Пример. Дан определитель .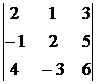

Вычислить минор и алгебраическое дополнение элемента .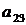

Решение. Вычислим минор элемента :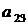

.

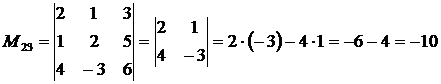Теперь вычислим алгебраическое дополнение элемента :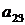

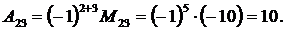
Ответ: ,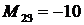

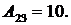
Любой определитель равен сумме произведений элементов произвольной строки (столбца) на их алгебраические дополнения. Этот способ вычисления определителя называется вычислением определителя с помощью разложения по строке (столбцу).

Пример. Вычислить определитель .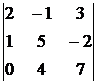

Решение. Вычислим этот определитель с помощью разложения по первой строке.

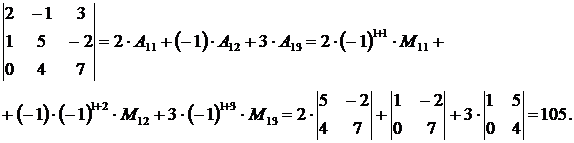
Такой же ответ получится, если определитель вычислять разложением по любой другой строке или столбцу.

Ответ: 105.

Обратная матрица

Матрица 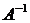называется обратной по отношению к квадратной матрице 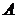, если выполняется равенство:

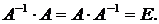(1)

Матрица 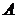имеет единственную обратную матрицу 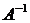тогда и только тогда когда ее определитель отличен от нуля.

Алгоритм вычисления обратной матрицы:

1. Вычислить определитель матрицы 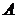. Если определитель этой матрицы равен нулю, то 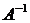не существует. Если же определитель этой матрицы не равен нулю, то 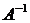существует.

2. Вычислить транспонированную матрицу .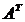

3. Вычислить алгебраические дополнения матрицы .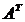

4. Вычислить обратную матрицу по формуле:

.

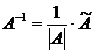5. Проверить правильность вычислений по формуле (1). Выполнение данного пункта не является обязательным.

Пример.Вычислить обратную матрицу 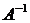, если

.

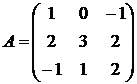Решение.

1. Вычислим определитель данной матрицы.

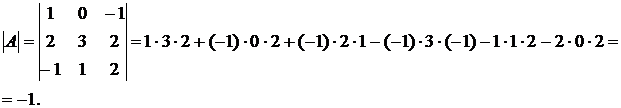
2. Вычислим транспонированную матрицу :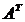

.

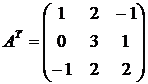3. Вычислим алгебраические дополнения матрицы :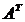

; ; ;

; ; ;

; ; .

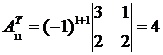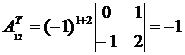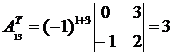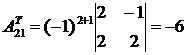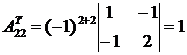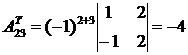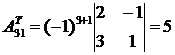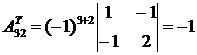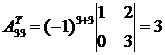4. Вычислим обратную матрицу:

.

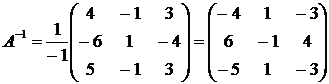Система линейных алгебраических уравнений (СЛАУ)

Основные понятия

Рассмотрим систему из m линейных уравнений с n переменными:

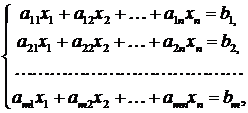(2)

где 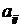– коэффициенты при переменных, 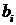– свободные члены уравнений.

Совокупность чисел 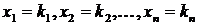называется решением системы (2), если при их подстановке каждое уравнение системы обращается в верное равенство.

Система, не имеющая решений, называется несовместной. Система, имеющая решения называется совместной.

Совместная система, имеющая единственное решение называется определенной. Совместная система, имеющая более одного решения называется неопределенной.

Выпишем коэффициенты при переменных в системе (2) в виде матрицы:

.

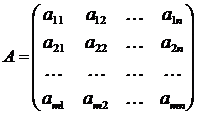Матрица 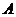называется матрицей системы.

Выписав из системы все переменные, получим матрицу-столбец переменных:

.

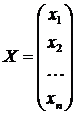Выписав все свободные члены, получим матрицу-столбец свободных членов:

.

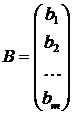Матрица

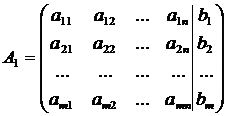
называется расширенной матрицей системы.

Метод Гаусса

Рассмотрим решение системы (2) методом Гаусса (методом последовательного исключения переменных). Метод Гаусса состоит из прямого и обратного хода.

Прямой ход. Выпишем расширенную матрицу системы (2) и приведем матрицу к ступенчатому виду, то есть к виду, для которого выполняются условия:

1) все ненулевые строки (имеющие, по крайней мере, один ненулевой элемент) располагаются над всеми чисто нулевыми строками;

2) ведущий элемент, то есть первый ненулевой элемент строки при отсчёте слева направо каждой ненулевой строки располагается строго правее ведущего элемента в строке, расположенной выше данной.

.

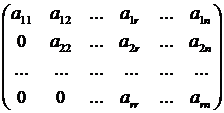Каждую прямоугольную матрицу с помощью элементарных преобразований можно привести к ступенчатому виду. Элементарные преобразования матрицы – это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, заданной с помощью этой матрицы.

К элементарным преобразованиям матрицы относится:

1) умножение любой строки на числовой коэффициент ;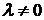

2) прибавление к какой-либо строке другой строки, умноженной на числовой коэффициент;

3) перестановка местами любых двух строк.

Обратный ход. Вернемся от расширенной матрицы ступенчатого вида к системе уравнений, которая соответствует этой матрице. Затем начиная с последних по номеру переменных, последовательно найдем все переменные.

Пример. Решить систему линейных уравнений:

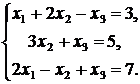
Решение. Решим эту систему уравнений методом Гаусса.

Выпишем расширенную матрицу и с помощью элементарных преобразований приведем ее к ступенчатому виду: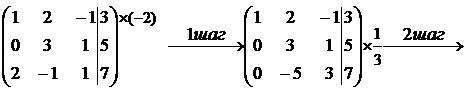

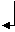
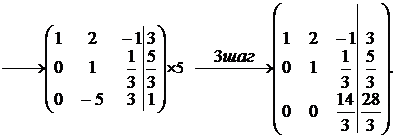
Прокомментируем каждый шаг алгоритма:

1-й шаг: умножаем первую строку на (-2) и прибавляем к третьей строке. В результате получим в первом столбце все нули, кроме верхнего элемента.

2-й шаг: умножим вторую строку на .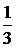

3-й шаг: умножим вторую строку на 5 и прибавим к третьей строке.

В результате мы получим расширенную матрицу ступенчатого вида.

Далее от полученной расширенной матрицы вернемся к соответствующей ей системе уравнений:

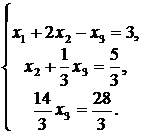
Отсюда, из третьего уравнения найдем 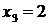. Подставляя полученное значение во второе уравнение, найдем 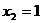. Подставляя вместо 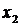и 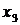полученные значения, из первого уравнения найдем .

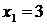Ответ: .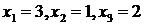

Формулы Крамера

Рассмотрим систему (2), в которой число уравнений равно числу переменных, то есть 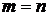. В этом случае матрица системы будет квадратной, а ее определитель называется определителем системы.

Если определитель матрицы системы 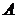не равен нулю 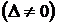, то система имеет единственное решение, которое определяется по формулам:

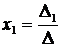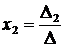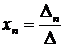, , …, , (3)

где 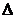− определитель матрицы системы,

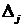− определитель, получаемый из определителя 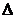заменой 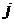- го столбца столбцом свободных членов.

Формулы (3) называются формулами Крамера.

Пример. Решить систему линейных уравнений:

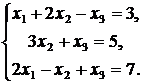
Решение. Решим систему линейных уравнений с помощью формул Крамера.

Составим определитель матрицы системы уравнений. Для этого выпишем коэффициенты при переменных 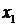, 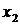и 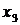в определитель и вычислим его по «правилу треугольника»:

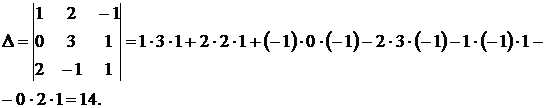
Заменив первый столбец определителя 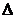столбцом свободных членов, получим определитель:

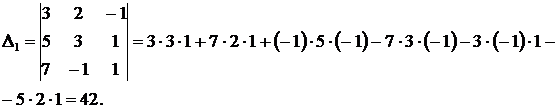
Заменив второй столбец определителя 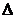столбцом свободных членов, получим определитель:

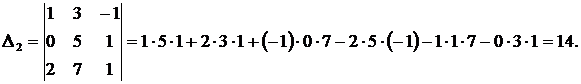Заменив третий столбец определителя 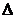столбцом свободных членов, получим определитель:

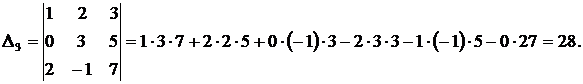
По формулам Крамера находим:

,

,

.

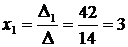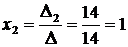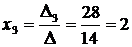Ответ: , , .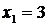

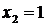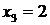Векторы и операции над ними

Вектором называется направленный отрезок, который можно перемещать параллельно самому себе. Векторы могут обозначается несколькими способами. Например, 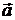либоa, или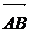, где точка 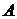означает начало вектора, а точка 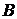– конец вектора.

Длиной вектора 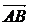называется число, равное длине отрезка 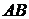, изображающего вектор. Длина вектора обозначается .

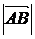Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными.

Вектор, длина которого равна нулю, называется нуль-вектором. Нуль-вектор обозначается .

Произведением вектора 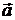на число 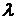называется вектор 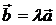, имеющий длину 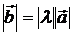, направление которого совпадает с направлением вектора 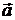, если 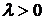, и противоположно ему, если .

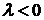Противоположным вектором называется вектор .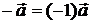

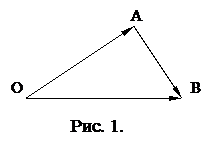Определим понятие суммы двух векторов. Пусть 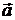и 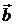– два произвольных вектора. Возьмем произвольную точку 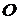и построим вектор 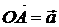. От точки 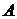отложим вектор 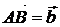. Вектор 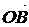, соединяющий начало первого вектора с концом второго, называется суммой векторов 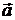и 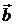: 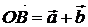. (см. рис. 1) Это правило сложения векторов называется правилом треугольника.

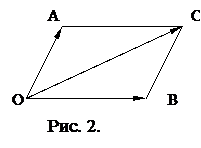
Также сумму двух векторов можно построить по правилу параллелограмма. Для этого берут произвольную точку 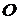и откладывают от нее два вектора 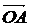и . Далее на этих векторах достраивают параллелограмм 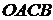. Диагональ 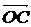является суммой векторов 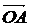и . (см. рис. 2)

Разностью двух векторов 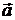и 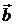называется вектор 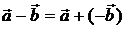. (см. рис. 3)

Введем понятие координат вектора. Для этого совместим начало вектора 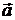с началом координат. Тогда координатами вектора 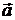называются координаты его конечной точки.

Пусть точка 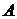имеет координаты 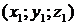, а точка 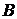– 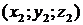. Тогда координаты вектора .

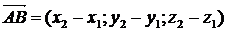Суммой векторов 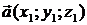и 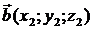является вектор .

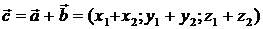Разностью векторов 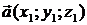и 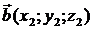является вектор .

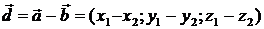Произведением вектора 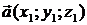на число 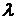называется вектор .

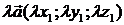Длина вектор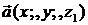а равна .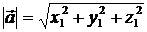

Скалярным произведением векторов 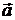и 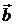называется число, равное произведению длин этих векторов на косинус угла между ними: 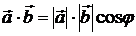, где 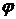– угол между векторам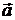и и .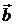

Если вектора 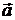и 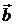заданы с помощью координат, то скалярное произведение векторов равно: .

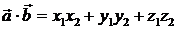Заметим, что скалярный квадрат вектора равен квадрату его длины: .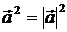

Угол между векторам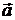и и 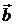вычисляется по формуле:

.

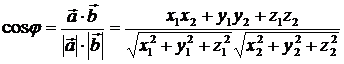Пример. Даны два вектора 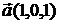и 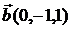. Найти угол между этими векторами.

Решение. Вычислим косинус угла между этими векторами: 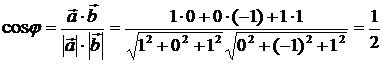. Следовательно, .

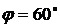Ответ: .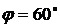

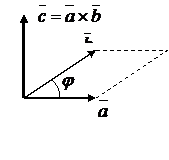Рис. 4.

Векторное произведение 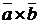(другое обозначение 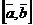) двух векторов 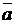и 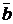есть третий вектор 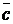, модуль которого 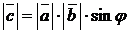(т. е. равен площади параллелограмма, построенного на векторах 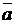и 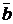), а направление перпендикулярно к обоим векторам 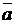и 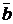(т. е. плоскости упомянутого параллелограмма) и совпадает с направлением поступательного движения правого винта при его повороте от 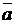к 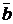на угол, меньший 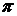. Из этого определения векторного произведения следует, что векторы 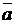, 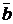и 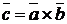образуют правую систему.

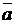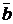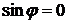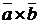Если векторы и коллинеарны ( ), то =0.

Свойства векторного произведения:

; ; ;

; .

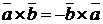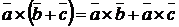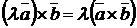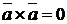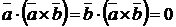Базисные единичные векторы декартовой прямоугольной системы координат удовлетворяют следующим соотношениям:

; ; ; .

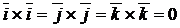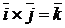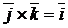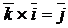Если векторы 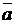и 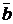заданы своими декартовыми координатами: 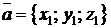, , 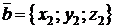то их векторное произведение

.

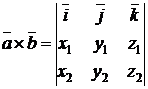Смешанным произведением векторовназывается произведение 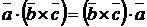, результатом которого является скаляр (число). Для компланарных векторов их смешанное произведение 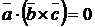. Если векторы 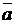, 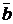и 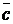образуют правую тройку, то 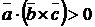, если – левую, то .

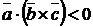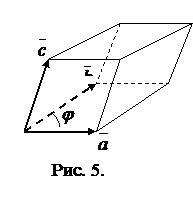Смешанное произведение 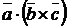равно объему параллелепипеда 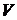, построенного на векторах 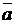, 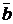и 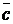, взятому со знаком «+», если векторы 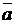, 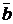и 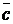образуют правую тройку, и со знаком «–», если – левую:

.

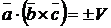Если векторы 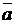, 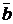и 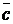заданы своими декартовыми координатами: 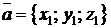, , 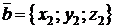, 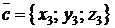то их смешанное произведение

.

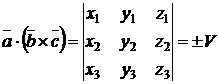Пример. Даны координаты вершин треугольника: 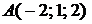, , 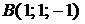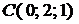. Найти площадь .

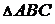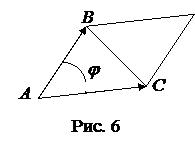Решение. Направим из вершины 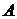треугольника векторы в вершины 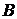и 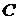(рис. 6). Учитывая, что площадь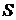 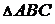равна половине площади параллелограмма, построенного на этих векторах, площадь которого, в свою очередь, можно выразить через векторное произведение, будем иметь 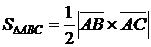. Находим координаты векторов: 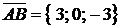, 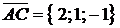. Находим векторное произведение = .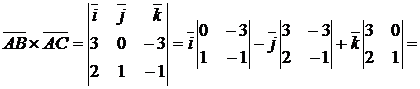

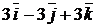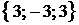Таким образом, 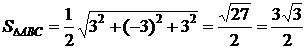(кв. ед.).

Пример. Найти объем параллелепипеда, построенного на векторах , , .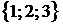

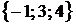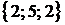Решение. Вычисляем смешанное произведение данных векторов: =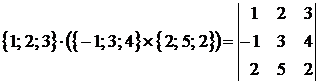

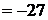. Объем параллелепипеда .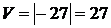