Начисление непрерывных процентов.

Пусть к началу года в нашем распоряжении имеется сумма Q₀ рублей. Как добиться к концу года максимального роста этой суммы? Один из способов – воспользоваться услугами банка.

Предположим, что банк дает 100% годовых; это означает, что за год хранения вклад возрастет на 100%. За любой меньший срок вклад возрастает пропорционально этому сроку (например, за один месяц прирост составит 100/12 процентов).

Итак, после года хранения, вклад станет 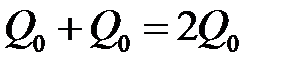, т.е. удвоится. Можно, однако, добиться большего эффекта, если по истечении полугода закрыть счет и тут же открыть его снова на очередные полгода. В этом случае к концу первого полугода вклад станет равным 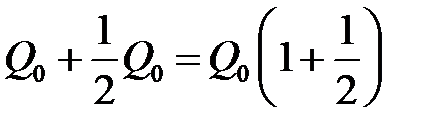, а к концу года будет равным .

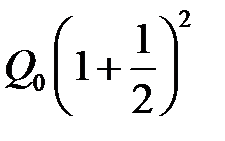Если операцию по закрытию и открытию счета производить чаще, то получим еще больший эффект: например, если эту операцию проводить в конце каждого месяца, то к концу года будем иметь 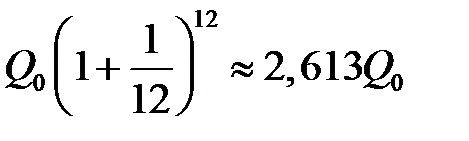, а если закрывать и открывать счет каждый день, то конечная сумма составит

.

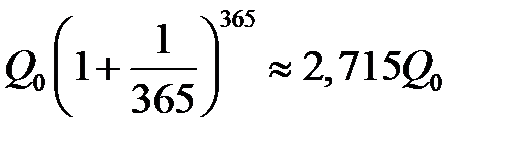Если представить, что операция закрытия-открытия производится непрерывно, то в итоге к концу года вклад составит

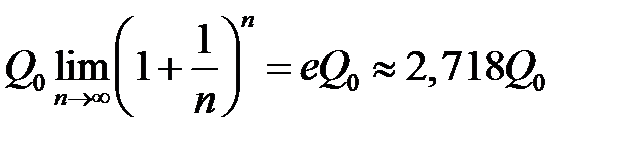руб.

Таким образом, при номинальной ставке 100% простые проценты дают двукратное повышение суммы вклада, а непрерывные увеличивают его в 2,718 раза.

Аналогично рассуждения можно провести для случая, когда номинальная ставка будет p% ( р/100). Тогда конечная ставка вклада будет равна

.

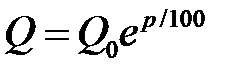Если вклад хранится не один год, а любое количество t лет, то получим формулу

,

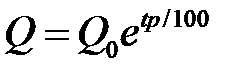Она называется формулой непрерывных процентов.

Пример 1. Определите какую сумму может получить вкладчик 500 тыс руб. через три года , если процентная ставка составляет 10% годовых при простом и непрерывном начислении процентов.

Прежде чем перейти к дифференциальному исчислению функции одной переменной, рассмотрим еще одну её характеристику, являющейся фундаментальной для последующего изучения.

3.5.Непрерывность функции.

Всякий раз, оценивая неизбежные с течением времени изменения в окружающем нас мире, мы пытаемся проанализировать происходящие процессы, чтобы выделить их наиболее существенные черты. Один из первых на этом пути встает вопрос: как происходят характерные для этого явления изменения – непрерывно или дискретно, т.е. скачкообразно. Чтобы унифицировать качественные и количественные оценки происходящего, следует абстрагироваться от конкретного содержания и изучить проблему в терминах функциональной зависимости. Это позволяет сделать теория пределов, которую мы рассматривали на прошлой лекции.

Непрерывность функции интуитивно связано с тем, что ее графиком является сплошная, нигде не прерывающаяся кривая. Мы вычерчиваем график такой функции, не отрывая ручки от бумаги.

В реальности при непрерывности имеет место следующее обстоятельство: если параметры, характеризующие ситуацию, немного изменить, то не много изменится и ситуация. Здесь важно не то, что ситуация изменится, а то, что она изменится «немного».

Сформулируем понятие непрерывности на языке приращений.

Пусть некоторое явление описывается функцией 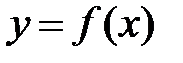и точка a принадлежит области определения функции. Разность 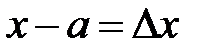называется приращением аргумента в точке a, разность 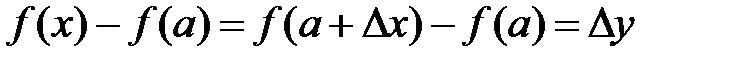– приращением функции в точке a.

Определение 1Функция 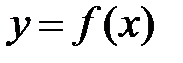непрерывна в точкеa, если она определена в этой точке и бесконечно малому приращению аргумента 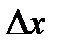соответствует бесконечно малое приращение функции :

.

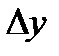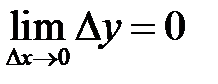Например, функция 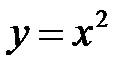непрерывна в точке 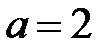и во всех точках её существования. Её график представляет собой сплошную линию (рис.5)

рис. 5.

Очевидно, что чем меньше приращение аргумента x, тем меньше приращение функции y.

Поскольку непрерывность функции играет важную роль, дадим более полное её определение на языке пределов.

Определение 2.Функция 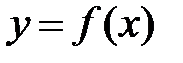называется непрерывной в точке а, если:

1) она определена в точке а, и некоторой ее окрестности;

2) односторонние пределы существуют и равны между собой:

;

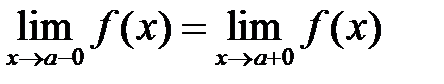3) предел функции при х®а равен значению функции в этой точке, т.е :

.

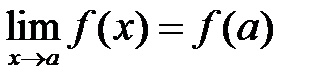Если хотя бы одно из этих условий нарушается, то говорят, что функция претерпевает разрыв. На рис. 6 – 8 показаны функции, имеющие разрыв.

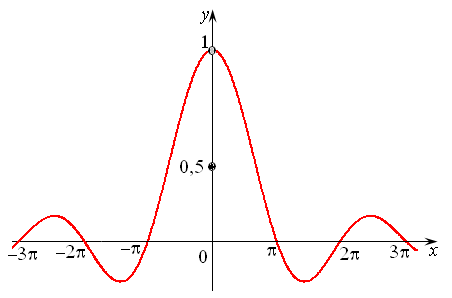
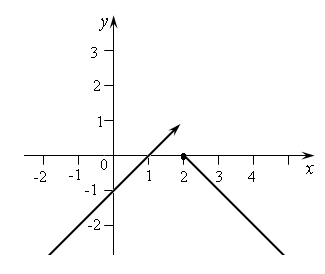
рис.6 рис.7

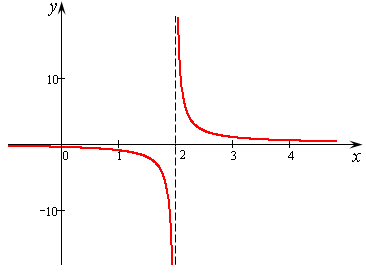
рис.8

В первом случае непрерывность нарушена в т. с координатами (0,1) – пустая или «выколотая» точка, что говорит о том, что функция в ней не определена. Доопределив эту функцию, т.е. положив дополнительно 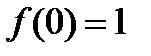, мы устраним этот разрыв. Поэтому такие точки называются точками устранимого разрыва.

Во втором случае (рис.7.) в т. х = 2 – функция претерпевает так называемый скачкообразный разрыв». Нарушено второе требование непрерывности: односторонние пределы существуют, но не равны между собой.

В третьем случае (рис.8.) в т. х = 2 функция претерпевает бесконечный разрыв. Оба односторонних предела не существуют. Точки ветвей их графиков уходят в .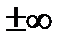

Пример 1. Построить график и определить характер

точек разрыва:

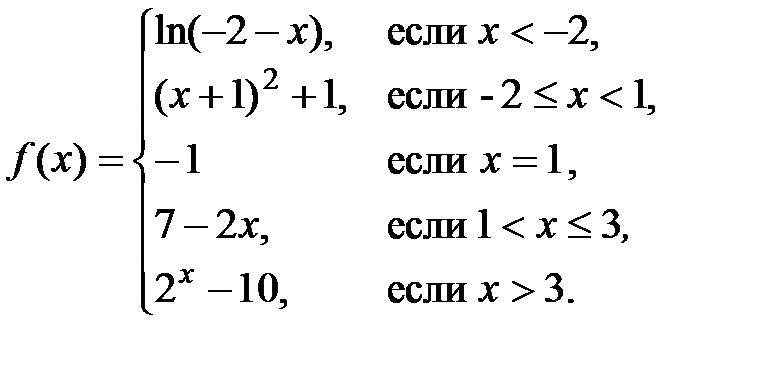
Решение. Построим график f(x) , предварительно протабулировав каждую функцию на ее интервале задания (рис 9).

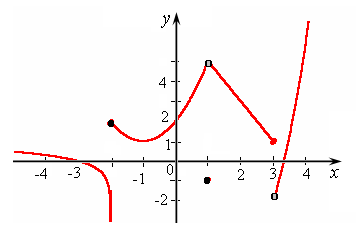
рис.9

Из рисунка видно, что исходная функция имеет три точки разрыва: 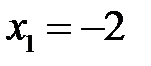, x₂ = 1, x₃ = 3. Рассмотрим их по порядку.

1. Пусть .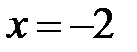

а) Функция определена в этой точке: .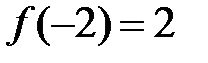

б) Найдем односторонние пределы, учитывая соответствующий вид функции: , .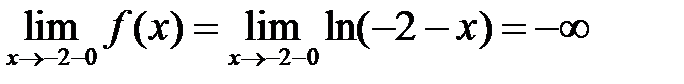

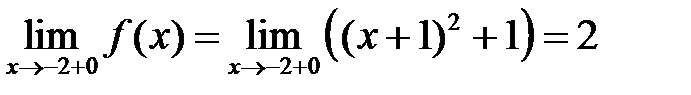Поэтому в точке 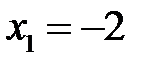разрыв 2-го рода.

2. Пусть .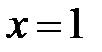

а) Функция определена в этой точке: f(1)=–1.

б) , ,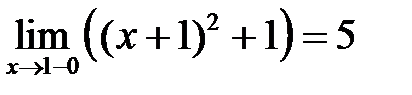

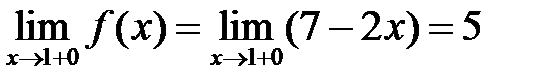т.е. в точке x₂ = 1 имеется устранимый разрыв. Переопределив значение функции в этой точке: f(1) = 5, разрыв устраняется и функция в этой точке становится непрерывной.

3. Пусть .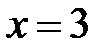

а) Функция определена в этой точке: f(3) = 1.

б) 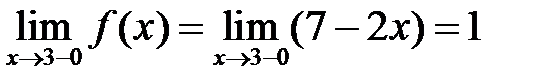, 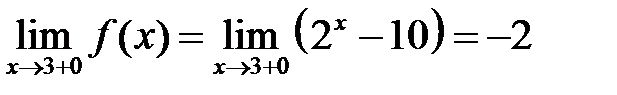Следовательно, в точке x₁ = 3 имеется разрыв 1-го рода. Функция в этой точке испытывает скачок, равный y = –2–1 = –3.