Интегральное и дифференциальное исчисление.
Многочисленные наблюдения и исследования показывают, что в окружающем нас мире величины (например, цена какого-либо товара и величина спроса на этот товар, прибыль фирмы и объем производства этой фирмы, инфляция и безработица и т.п.) существуют не изолированно друг от друга, а, напротив, они связаны между собой определенным образом. Понятие функции или функциональной зависимости – одно из основных математических понятий, при помощи которых моделируются взаимосвязи между различными величинами, количественные и качественные отношения между различными экономическими показателями и характеристиками. Этими и многими другими вопросами занимается математический анализ.
Из школьного курса математики известно, что функцией называется закон, по которому значениям одной переменной «х» из множества М ( х) ставятся в соответствие значения другой переменной «у» из множества I( у). Функция может быть задана аналитически с помощью одного или нескольких выражений, графически или таблично.
Если функция задана аналитически,то под областью ее определения М(х) (или областью существования) понимаются те действительные числа , при которых аналитическое выражение f(x) не теряет числового смысла и принимает только действительные значения. Поэтому из полного числового множества 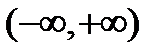 исключаются точки, где:
исключаются точки, где:
1.знаменитель дроби равен нулю;
2. подкоренное выражение для радикалов четных степеней отрицательно (меньше нуля);
3. выражение, стоящее под знаком логарифма, меньше либо равно нулю.
Например
1) Функция 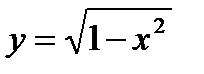 имеет областью определения отрезок
имеет областью определения отрезок 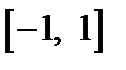 , где подкоренное выражение неотрицательно.
, где подкоренное выражение неотрицательно.
2) Функция 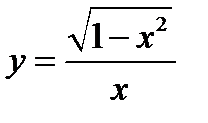 определена на двух полуинтервалах [–1, 0) и (0, 1].
определена на двух полуинтервалах [–1, 0) и (0, 1].
3) Функция 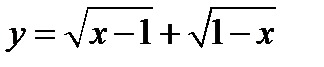 определена только при х = 1. Первое слагаемое определено на полуинтервале [1,
определена только при х = 1. Первое слагаемое определено на полуинтервале [1, 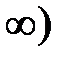 , а второе также на полуинтервале на
, а второе также на полуинтервале на 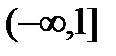 . Их объединение и дает точку х = 1.
. Их объединение и дает точку х = 1.
4) Функция 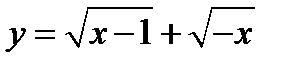 не определена ни при каком х, так как
не определена ни при каком х, так как 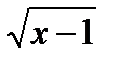 существует при
существует при 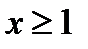 , а
, а 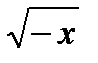 – если
– если 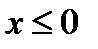
Если областью изменения функции y = f ( x ) являются все значения (– 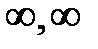 ), то ее называют неограниченной. Если
), то ее называют неограниченной. Если 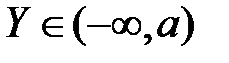 , то ее называют ограниченной сверху,
, то ее называют ограниченной сверху, 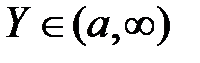 , то она ограничена снизу и если
, то она ограничена снизу и если 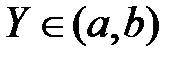 то ее называют просто ограниченной (рис.1).
то ее называют просто ограниченной (рис.1).
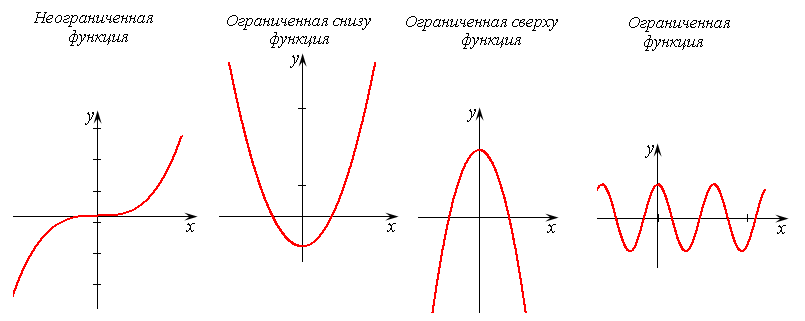
рис. 1
Напомним, что функции могут быть четными, нечетными и общего вида.
Функция называется четной, если для нее выполняется равенство: 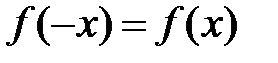 , и нечетной, если
, и нечетной, если 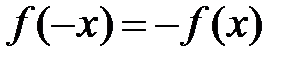 . Четная функция симметрична относительно оси ОY, нечетная – относительно начала координат.
. Четная функция симметрична относительно оси ОY, нечетная – относительно начала координат.
Примером четной функции является степенная функция вида 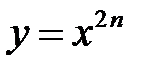 , т.е. с четным показателем степени, а нечетная – с нечетным показателем степени –
, т.е. с четным показателем степени, а нечетная – с нечетным показателем степени – 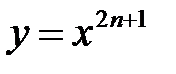 .
.
Кроме того, функции могут быть периодическими и непериодическими. Функция называется периодической, если существует такое положительное число Т, что для всех x из области определения выполняется равенство 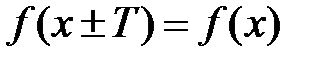 К периодическим, в основном, относятся тригонометрические функции.
К периодическим, в основном, относятся тригонометрические функции.
Из школьного курса известно, что функции 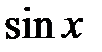 ,
, 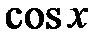 имеют минимальный период, равный 2
имеют минимальный период, равный 2 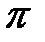 , а
, а 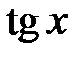 ,
, 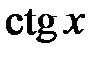 – период
– период 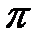 .
.
Задачи для повторения:.
1.Областью определения функции 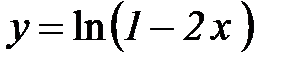 , является множество …
, является множество …
1) 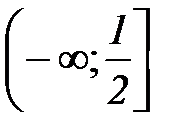 2)
2) 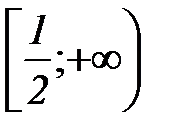 3)
3) 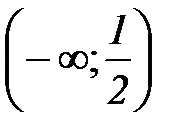 4)
4) 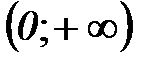
2.Область определения функции 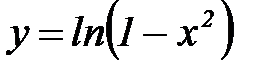 запишется в виде…
запишется в виде…
1) 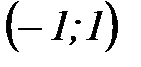 2)
2) 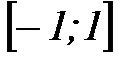 3)
3) 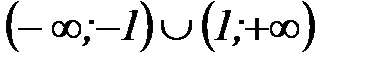 4) 15
4) 15
3.Область определения функции 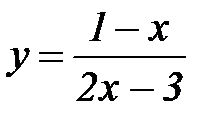 запишется в виде…
запишется в виде…
1) 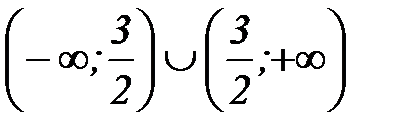 2)
2) 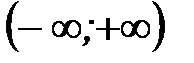 3)
3) 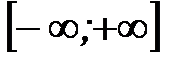 4)
4) 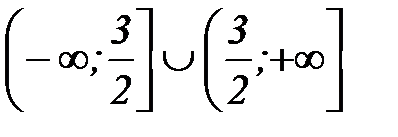
4.Наименьшее значение 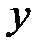 из области значения функции
из области значения функции 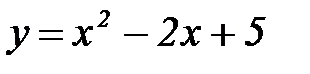 равно …
равно …
1) 6 2) 3 3) 4 4) 5
5. Область определения функции 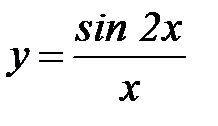 запишется в виде…
запишется в виде…
1) 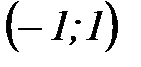 2)
2) 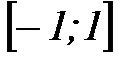 3)
3) 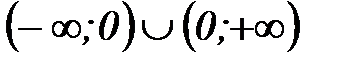 4)
4) 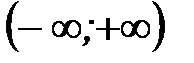
Ответы. 1) 1, 2) 3, 3) 1 4) 2 5) 3
Предел функции
4.1. Основные понятия и определения.
Одним из основополагающих понятий математического анализа является понятие предела функции f(x) при стремлении аргумента « x» к некоторой точке а или к бесконечности.
Выражение 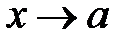 означает, что переменная х неограниченно приближается к точке а, но никогда ее не достигает, т.е. разность
означает, что переменная х неограниченно приближается к точке а, но никогда ее не достигает, т.е. разность 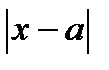 по модулю будет сколь угодно малой величиной и стремиться к нулю. В этом случае пишут
по модулю будет сколь угодно малой величиной и стремиться к нулю. В этом случае пишут 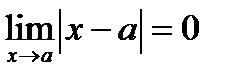
Выражение 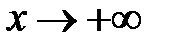 означает, что переменная х становится как угодно большой величиной, неограниченно удаленной от начала координат. В этом случае пишут
означает, что переменная х становится как угодно большой величиной, неограниченно удаленной от начала координат. В этом случае пишут 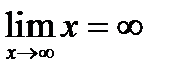 . Начнем тему «Теория пределов» с понятий бесконечно малых и бесконечно больших функций.
. Начнем тему «Теория пределов» с понятий бесконечно малых и бесконечно больших функций.
