Определение необходимого числа измерений при преобладании случайной погрешности.

При подготовке эксперимента часто возникает задача: определить, сколько потребуется выполнить измерений n, чтобы с заданной надежностью γ погрешность результата не превышала установленного предельного значения δ.

Предельная доверительная погрешность δ для заданной надежности при большом количестве измерений (n≥30) вычисляют по формуле

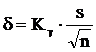
Отсюда следует, что, когда число измерений велико (n≥30),их приблизительное значение можно определить по формуле 5.23.

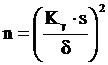. (5.23)

Предельная доверительная погрешность δ для заданной надежности при малом количестве измерений (n<30) вычисляют по формуле

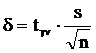
Отсюда следует, что, когда число измерений мало (n<30),их приблизительное значение можно определить по формуле 5.24.

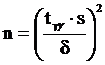. (5.24)

5.1.9 Правила определения необходимого числа измерений для получения заданной точности результата.

1. По результатам предыдущих измерений, проведенных примерно в тех же условиях, определяют значение стандартного отклонения s. Если это невозможно, то проводят небольшое выборочное наблюдение специально для оценки s.

2. Задают значение надежности γ и требуемую предельную погрешность δ.

3. По таблице для интеграла вероятности находят значение коэффициента К_γ из условия

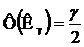
При γ = 0,95 К_γ =0,1808; γ = 0,959 К_γ =0,1879; γ = 0,999 К_γ =0,1915.

4. Вычисляют необходимое число измерений

.

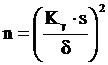5. Если окажется, что найденное число n<30, то полученное значение уточняют. Для чего по таблице находят значение коэффициента Стьюдента t_γ,ν для заданной надежности γ и числа степеней свободы ν=(n-1) и проверяют, выполняется ли равенство

.

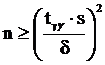Если условие в п.5 не выполнено, то увеличивают n до тех пор, пока оно не начнет выполняться, определяя каждый раз заново значение t_γ,ν. Получившееся при такой процедуре n и есть искомое число измерений.

5.2 Представление численных результатов измерений

Получаемое в результате измерения число никогда не является точным значением измеряемой величины, оно всегда содержит ошибку.

В качестве оценки чаще всего используют наиболее вероятное значение, а для представления результата обычно используют полную или сокращенную форму записи.

1. Полная форма записи (Рекомендуется как основная в ГОСТ 8.011-72. ГСИ. Представление результатов измерений) Полная форма записи изображена на рисунке 5.3.

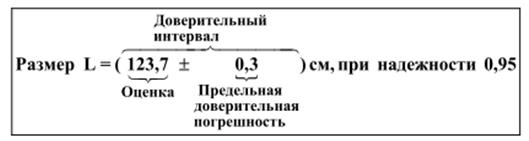
Рисунок 5.3 - Полная форма записи измерений

или в виде двойного неравенства (рисунок 5.4).

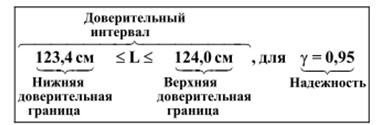
Рисунок 5.4 - Полная форма записи измерений в виде двойного неравенства

Как понимать такую запись: Истинное значение измеряемой величины находится в указанном доверительном интервале с вероятностью не менее 0,95.

Сокращенная форма записи

Табличная форма записи

Размер L = 123,7 см, (5.25)

Или сокращенная форма записи без указания надежности:

Размер L = 123,7 ± 0,3 см, (5.26)

Встретив такую форму записи, вы должны решить какой надежности соответствует указанная погрешность (± 0,3):

А) Автор считает свой результат практически достоверным (погрешность равна трем стандартными ошибкам (±3σ)), что соответствует надежности γ=0,9973.

Б) Автор использовал наиболее вероятную ошибку, что соответствует надежности γ=0,5. В таком случае погрешность равна стандартной ошибке, умноженной на 0,6750.

В) Автор указал погрешность в одну стандартную ошибку, что соответствует надежностиγ=0,6750.

Г) Автор не знаком с теорией ошибок измерений.