Сложение и вычитание векторов

Линейными операциями над векторами называется сложение, вычитание векторов и умножение вектора на число.

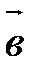Результатом сложения векторов является их сумма. Сумма векторов и обозначается .

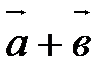Существует два правила сложения двух векторов: правило треугольника и правило параллелограмма.

Правило треугольника

Чтобы сложить векторы и 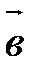, надо взять произвольную точку и от нее отложить последовательно сначала вектор , затем вектор 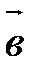. Вектор, начало которого совпадает с началом вектора (т.е. первого вектора), а конец – с концом вектора 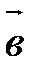(т.е. второго вектора), есть искомая сумма. На рис. 4 .

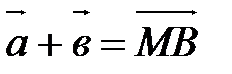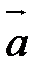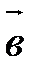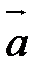М

В

Рис. 4

По правилу треугольника можно складывать любые векторы.

Коротко правило треугольника можно записать так:

для любых трех точек А,В и С .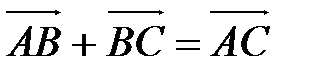

Правило параллелограмма

Чтобы сложить векторы и 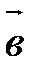, надо привести их к общему началу, т.е. взять произвольную точку А, построить такие точки В и С, что 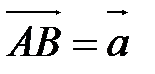и 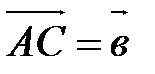, и достроить полученную фигуру до параллелограмма 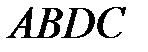. Вектор 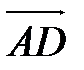- искомая сумма (рис. 5).

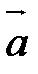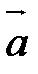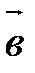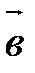А

С

В

D

Рис. 5

По правилу параллелограмма можно складывать тольконеколлинеарные векторы.

Свойства сложения векторов:

1⁰. .

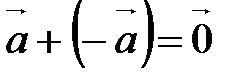
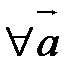2⁰. .

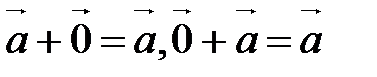
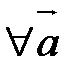3⁰. .

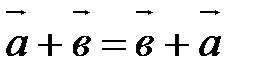
4⁰. .

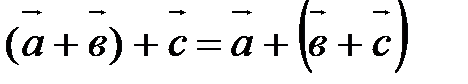
Суммой трех векторов 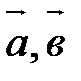и 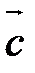называется вектор 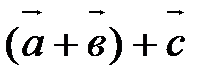. Учитывая свойство 4⁰, скобки можно опустить и обозначать сумму в виде .

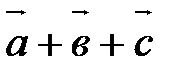Суммой nвекторов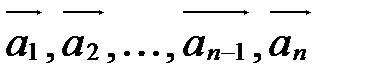называется вектор 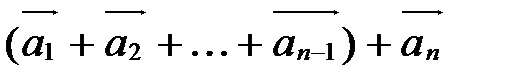и обозначается так: .

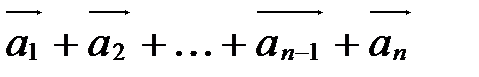При построении суммы n векторов пользуются правилом многоугольника.

Правило многоугольника

Чтобы найти сумму nвекторов, надо взять произвольную точку и отложить от нее последовательно эти векторы. Вектор, начало которого совпадает с началом первого вектора, а конец – с концом последнего (n-го вектора), есть искомая сумма.

Разностью векторов и 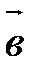называется такой вектор 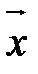, что 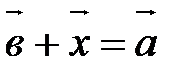. Разность – это результат вычитания векторов. Разность векторов и 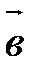обозначается так: .

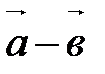Правило построения разности двух векторов

Чтобы построить разность векторов и 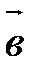, надо привести их к общему началу. Тогда вектор, начало которого совпадает с концом второго вектора (т.е. вектора 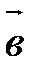), а конец – с концом первого (т.е. ), есть искомая разность .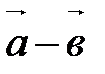

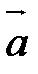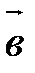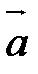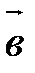Р

М

Рис. 6

На рис. 6 .

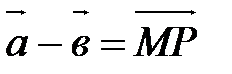По правилу треугольника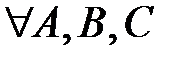

,

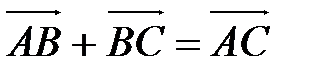откуда получаем краткую запись правила нахождения разности векторов:

.

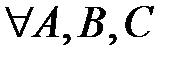
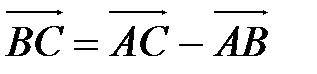Умножение вектора на число

Рассмотрим еще одну линейную операцию над векторами – умножение вектора на число. Результатом этой операции является произведение вектора на число.

Произведением вектора на действительное число a называется вектор 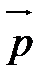, обозначаемый через 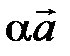и удовлетворяющий двум условиям:

1) его длина ;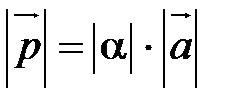

2) если a 0, то 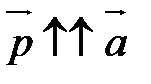; если 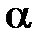<0, то .

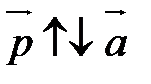Алгоритм построения произведения вектора числоa таков.

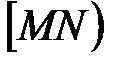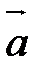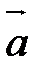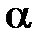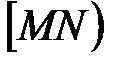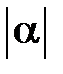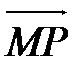Берем произвольную точку М. Проводим луч ,сонаправленный с вектором , если a 0, и противоположно направленный с вектором , если <0. На луче от начала М откладываем отрезок MP, длина которого в раз больше длины вектора .Вектор - искомый вектор .

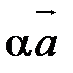Продемонстрируем этот алгоритм на конкретном примере. Построим вектор 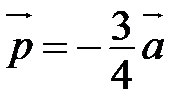, если - данный вектор.

Возьмем произвольную точку А. Так как 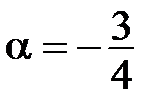<0, то проводим луч 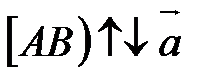(рис. 7). На луче 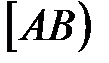строим такую точку С, что 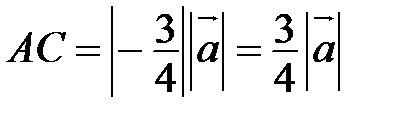. Тогда 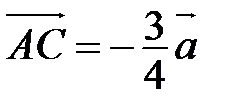- искомый вектор.

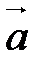А

С

В

Рис. 7