Расчет САР напряжения генератора постоянного тока (задача 3).

В системе автоматического регулирования напряжения генератора (рис.4) используются элементы, параметры которых приведены в табл. 4. Во всех вариантах генератор имеет следующие параметры: U_н = 220 В, ω_н = 78,5 рад/с, 2р = 4; 2а = 2. Коэффициент передачи датчика напряженияR2К_ф = 0,04. Диапазон регулирования D = 1.

Рис.4. Принципиальная схема САР напряжения генератора

Таблица 4

Параметры элементов САР напряжения генератора

Вариант	Генератор	Тиристорный преобразователь	Фильтр	Точность регулирования
Iн, А	rя, Ом	wя	rв, Ом	Iвн, А	wв	Lн, мГн	TТП, с	Тф, с	δ, %
		0,018		19,5	11,3		0,92	0,006	0,01	0,5
		0,038			10,5		1,34	0,007	0,015
		0,057			9,21		2,34	0,008	0,01	0,5
		0,078			7,08		5,20	0,006	0,015
		0,089		32,5	8,77		8,3	0,007	0,02	0,5
		0,11		37,8	5,02		8,9	0,008	0,01	1,5
		0,12		48,4	4,55		9,3	0,006	0,015
		0,13		35,8	6,15		10,5	0,007	0,02	0,5
		0,11		40,4	5,45		9,2	0,008	0,01	0,5
		0,099		42,1	5,23		7,45	0,009	0,015

Коэффициент передачи регулятора напряжения (РН) должен обеспечить статическую ошибку САУ меньше заданной во всем диапазоне регулирования при изменении сопротивления нагрузки генератора от 1,0 до 5,0 r_н.Выполнить расчет параметров РН на основе регулирующего усилителя (см. рис.2) аналогично приведенному в задаче 1.

1.4. Расчет САР тока генератора постоянного тока( задача 4)

В системе автоматического регулирования тока генератора (рис.5) используются элементы, параметры которых приведены в таблице к задаче 3. Коэффициент передачи датчика тока указан в табл. 5.

Рис. 5. Принципиальная схема САР тока генератора

R2 – датчик тока (измерительный шунт)

Таблица 5.

Значения коэффициента передачи датчика тока

Вариант
КДТ, мВ/А

Коэффициент передачи регулятора тока (РТ) должен обеспечить статическую ошибку САР меньше заданной во всем диапазоне регулирования при изменении напряжения на нагрузке от 1,0 до 5,0 r_н. Выполнить расчет параметров РТ на основе регулирующего усилителя (см. рис.2) аналогично приведенному в задаче 1.

Методика выполнения курсового проекта

Задача 1

1.Уравнение равновесия напряжений якорной цепи двигателя:

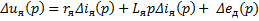(1)

где 𝛥i_я(p) изображение тока якоря двигателя

r_я = r_яд + r_тп + r_др - полное сопротивление якорной цепи двигателя;

r_яд - сопротивление якорной цепи двигателя;

r_тп - сопротивление тиристорного преобразователя, включающее приведенное активное сопротивления обмотки трансформатора и дифференциальное сопротивление тиристоров;

r_др - сопротивление сглаживающего дросселя;

L_я = L_яд + L_тр + L_др - суммарная индуктивность якорной цепи двигателя;

L_яд - индуктивность якоря двигателя;

L_тр – индуктивность обмотки трансформатора;

L_др - индуктивность сглаживающего дросселя;

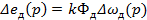- приращение ЭДС двигателя.

Уравнение равновесия моментов двигателя:

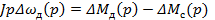, (2)

где 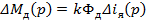- приращение момента двигателя;

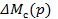- приращение момента сопротивления;

J=J_я +J_н- сумма момента инерции двигателя и нагрузочного механизма.

Решая систему уравнений (1) и (2) относительно 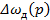и вводя постоянные времени цепи якоря Т_я и электромеханическую Т_эм, получим:

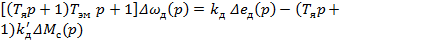(3)

где T_я=L_я/r_я – постоянная времени цепи якоря;

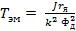– электромеханическая постоянная времени;

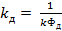- коэффициент передачи двигателя по управлению;

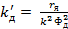- коэффициент передачи двигателя по возмущению.

Уравнение тиристорного преобразователя, работающего в режиме непрерывного тока, упрощенно можно записать так:

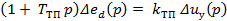(4)

где T_ТП=τ+T_ф - эквивалентная постоянная времени тиристорного преобразователя;

T_ф- постоянная времени фильтра;

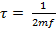- среднестатическое запаздывание преобразователя, связанное с числом фаз сети m и частотой f;

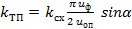- коэффициент передачи ТП по управлению (рис.5).

Для системы управления, имеющей пилообразную форму опорного напряжения с максимальным опорным напряжением 12 В, и мостовой трехфазной схемы ТП

k_ТП = 39,1 sinα

Уравнения тахогенератора и потенциометра

𝛥u_ТГ(p) = k_ТП𝛥ω_ТГ(p) (5)

𝛥u_П(p) = k_П𝛥u_ТГ(p) (6)

где k_ТГ- коэффициент передачи тахогенератора;

k_П - коэффициент передачи потенциометра.

Регулятор частоты вращения осуществляет пропорциональный закон регулирования, и его уравнение

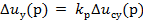(7)

где u_су – выходное напряжение сравнивающего устройства

u_у – выходное напряжение регулятора скорости

k_р – коэффициент передачи регулятора скорости

Решая систему уравнений (1) – (7) и исключая промежуточные переменные величины, получим уравнение разомкнутой системы:

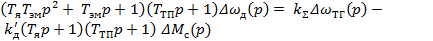(8)

Передаточная функция разомкнутой системы по управлению

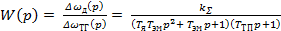(9)

где k_Σ=k_дk_ТПk_рk_Пk_ТГ - коэффициент передачи системы.

Передаточная функция по возмущению

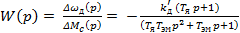(10)

Уравнение замкнутой системы получим, если в уравнении (8) положим

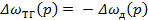
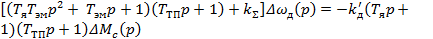(11)

На рис.6 приведена структурная схема, построенная по уравнениям отдельных звеньев системы.

Рис.6. Структурная схема САР частоты вращения двигателя

2.Найдем изменение частоты вращения 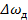для установившегося режима, положив p = 0,

в разомкнутой САР по уравнению (8), ,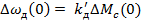

а в замкнутой САР по уравнению (11) .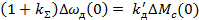

Для обеспечения заданной точности поддержания постоянства частоты вращения электродвигателя на всем диапазоне регулирования коэффициент передачи системы определяется из условия работы на минимальной частоте вращения ω_min. Тогда связь между максимальным коэффициентом передачи системы k_Σ, требуемой точностью δ и диапазоном регулированииD частоты вращения электродвигателя, будет

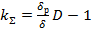(12)

где 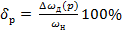- относительное изменение частоты вращения электродвигателя в разомкнутой системе, вызванное изменением его нагрузки ;

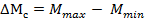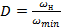- диапазон регулирования частоты вращения.

Коэффициент усиления регулятора скорости

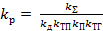(13)

Статическую ошибку САР меньше заданной позволяет получить пропорциональный регулятор.Схемастандартного регулирующего усилителя на основе операционного усилителя приведена на рис.2.Выбрать необходимые резисторы для полученного значения коэффициента передачи регулятора можно по номинальным данным сопротивлений резисторов, которые приведены в таблице 3.

3.Характеристическое уравнение замкнутой системы регулирования

,

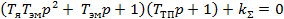общий вид уравнения после раскрытия скобок:

a₀p³ + a₁p² + a₂p + a₃ = 0

где a₀ = T_я T_эм T_ТП; a₁ = T_я T_эм + T_эм T_ТП

a₂ = T_эм + T_ТП; a₃ = 1 + k_Σ

Для устойчивости линейной системы третьего порядка в соответствии с критерием Гурвица необходимо и достаточно, чтобы:

а) коэффициенты характеристического уравнения были положительны:

a₀> 0; a₁> 0; a₂> 0; a₃> 0

б) выполнялось неравенство:

a₁a₂ – a₀a₃> 0

Система находится на грани устойчивости, если

a₁a₂ – a₀a₃ = 0

Подставив значения коэффициентов, получим:

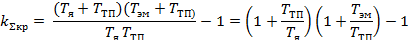
3.2. Задача 2

1.Уравнения равновесия напряжения возбуждения двигателя

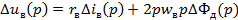(14)

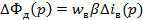(15)

где r_в - сопротивление обмотки возбуждения двигателя;

w_в - число витков обмотки возбуждения;

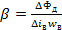- коэффициент пропорциональности между потоком и магнитодвижущей силой.

Определяется по универсальной кривой намагничивания двигателей постоянного тока (рис.8), которая построена в относительных единицах; за базовые приняты номинальные значения,

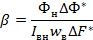
Номинальный поток определяется по выражению:

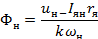
где 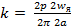- конструктивная постоянная двигателя.

Рис.8. Кривая намагничивания

Уравнение равновесия моментов двигателя:

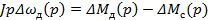
где 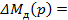kI_яΔФ_д(p) - приращение моментов двигателя;

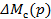- приращение момента сопротивления.

Решая систему уравнения (14), (15) и (16) относительно Δω_д(p) и вводя постоянную времени возбуждения Т_в, получим:

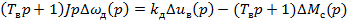, (18)

где 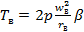– постоянная времени обмотки возбуждения

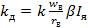- коэффициент передачи двигателя по управлению.

Уравнения тиристорного преобразователя, тахогенератора, потенциометра и регулятора скорости смотри в задаче 1.

Решая систему уравнений (4) - (7) и(17), и исключая промежуточные переменные, получим уравнение разомкнутой САР:

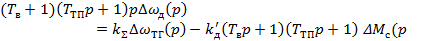
Передаточная функция разомкнутой системы по управлению

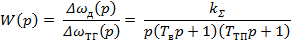
где 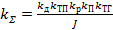- коэффициент передачи системы.

Передаточная функция по возмущению

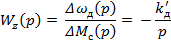
где 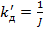- коэффициент передачи двигателя по возмущению.

Уравнение замкнутой системы получим, если в уравнении (18) положим

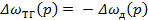
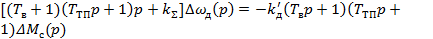(19)

На рис.9 приведена структурная схема САР, построенная по уравнениям отдельных звеньев системы.

Рис.9. Структурная схема САР частоты вращения двигателя

2.Найдем изменение частоты вращения 𝛥𝜔_д для установившегося режима, положив p = 0, в замкнутой САР по уравнению (19):

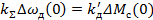
Относительная статическая ошибка регулирования, определенная из условия работы на минимальной частоте вращения ω_min,

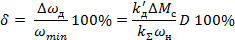
Необходимый коэффициент передачи системы

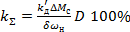,а коэффициент усиления регулятора скорости

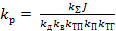(20)

3.Характеристическое уравнение замкнутой САР

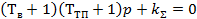(21)

Общий вид уравнения после раскрытия скобок:

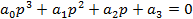
где ; ; ;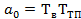

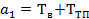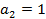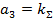
Заменяя в характеристическом уравнении (21) замкнутой системы регулирования оператор p = j𝜔, получим выражение для характеристической кривой Михайлова:

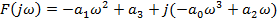
Задаваясь значениями частоты от ω = 0 до ω = ∞ и вычисляя вещественную и мнимую части характеристического вектора, строим по точкам кривую Михайлова. Если кривая, начинаясь с вещественной оси пересекает последовательно nквадрантов (в данном случаеn = 3), то САР устойчива.

Если кривая Михайлова в своем движении проходит через начало координат, то система находится на грани устойчивости, и, следовательно, критический коэффициент передачи можно определить так:

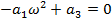
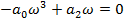
Из второго уравнения найдем критическую частоту:

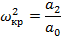
Подставив полученное выражение в первое уравнение, получим:

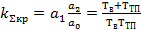(22)

3.3. Задача 3

При составлении уравнений генератора реакцией якоря, нелинейностью характеристики, влиянием вихревых токов и компенсационных обмоток пренебрегаем.

Уравнение равновесия напряжений якорной цепи генератора:

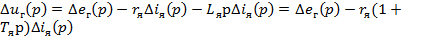(23)

Уравнение цепи нагрузки генератора:

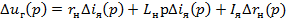(24)

Исключая промежуточную переменную – ток якоря – получим уравнение напряжения генератора:

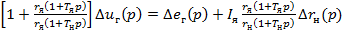(25)

или

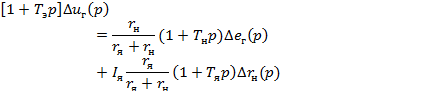
где r_я, r_н, L_я,L_н - сопротивления и индуктивности якорной цепи генератора и нагрузки, соответственно.

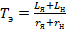- эквивалентная постоянная времени якорной цепи

Уравненияцепи обмотки возбуждения:

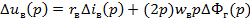
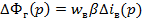
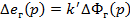
Решая совместно, получим:

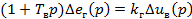(26)

где 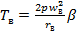- постоянная времени обмотки возбуждения;

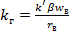- коэффициент передачи генератора по возбуждению;

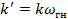
𝛽- коэффициент пропорциональности между потоком и магнитодвижущей силой (смотри задачу 2).

Уравнение RC-цепи (фильтра):

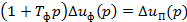(27)

где T_ф = RC- постоянная времени фильтра.

Уравнения тиристорного преобразователя и регулятора напряжения смотри в задаче 1.

Решая систему уравнений (23-25), (4), (6) и (7) и исключая промежуточные переменные, получим уравнение разомкнутой системы:

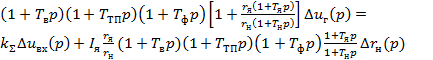(28)

где k_Σ= k_гk_ТПk_рk_П - коэффициент передачи системы.

Передаточная функция разомкнутой системы по управлению

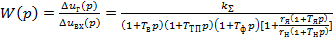(29)

Передаточная функция по возмущению

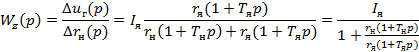
Уравнение замкнутой системы получим, если в уравнении (28) положим

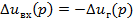
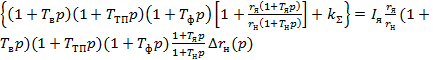(30)

Характеристическое уравнение замкнутой САР

,

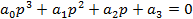где коэффициенты характеристического уравнения a₀, a₁, a₂ и а₃ определяются из уравнения

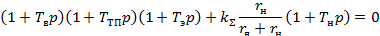
На рис.10 приведена структурная схема, построенная по уравнениям отдельных звеньев системы.

Рис.10. Структурная схема системы регулирования

2.Найдем изменение напряжения генератора 𝛥u_г(p) для установившегося режима, положив p = 0, в замкнутой САР по уравнению (30):

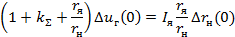
Относительная статическая ошибка регулирования, определенная из условия работы при минимальном напряжении

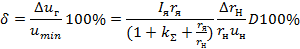
Необходимый коэффициент передачи системы

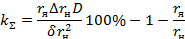
а коэффициент усиления регулятора напряжения

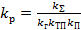(31)

3.Для определения устойчивости системы частотным критерием Найквиста необходимо построить амплитудно-фазовую частотную характеристику разомкнутой САР. Заменяя в (29) p = j 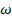получим комплексный коэффициент передачи:

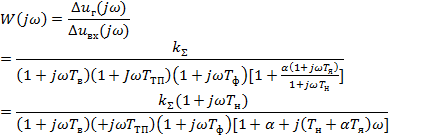
где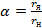

Построим характеристику по отдельным звеньям системы:

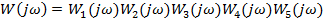
где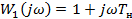

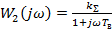
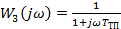
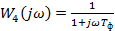
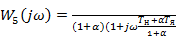
Так как САР состоит из устойчивых звеньев, соединенных последовательно и, следовательно, разомкнутая система устойчива, то замкнутая система будет устойчива, если АФЧХ не охватывает критическую точку с координатами (-1, j0).

Критический коэффициент передачи системы

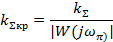
где ω_π - частота, при которой АФЧХ пересекает отрицательную вещественную ось.

3.4. Задача 4

1.При составлении уравнений генератора, реакцией якоря, нелинейностью характеристики, влиянием вихревых токов и компенсационных обмоток пренебрегаем.

Уравнение равновесия напряжения якорной цепи генератора (23) и уравнение цепи нагрузок генератора (24) решаем относительно тока якоря:

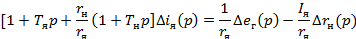
Преобразовав уравнение генератора, получим:

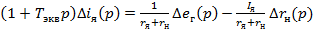(32)

Уравнения цепи возбуждения генератора (26), тиристорного преобразователя (4), регулятора тока (7) получены ранее; уравнение датчика тока

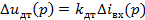(33)

Решая системы уравнений (4), (7), (26), (32), (33) относительно тока якоря, получим уравнение разомкнутой системы:

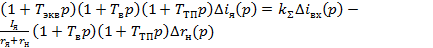(34)

Передаточная функция разомкнутой системы по управлению

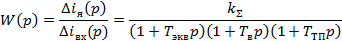
где 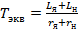- эквивалентная постоянная времени;

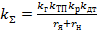- коэффициент передачи САР;

L_я - индуктивность якоря генератора определяется по уравнению (1).

Передаточная функция по возмущению

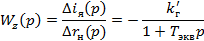
где 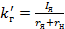- коэффициент передачи генератора по возмущению.

Уравнение замкнутой системы получим, приравняв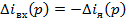

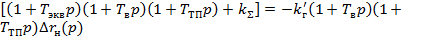(36)

На рис.11 приведена структурная схема, построенная по уравнениям отдельных звеньев системы.

Рис. 11. Структурная схема системы регулирования\

2.Найдем изменение тока генератора для установившегося режима, положив p = 0, в замкнутой САР по уравнению (36):

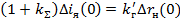
Относительная статическая ошибка регулирования, определенная из условия работы при максимальном токе,

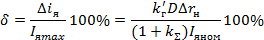
Коэффициент передачи системы, необходимый для поддержания заданной точности.

,

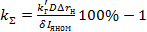а коэффициент усиления регулятора тока

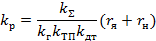
3.Так как система состоит из последовательно включенных устойчивых звеньев и не содержит внутренних обратных связей, то в разомкнутом состоянии она будет устойчивой.

Для определения устойчивости в замкнутом состоянии необходимо построить логарифмические амплитудные и фазовые характеристики разомкнутой САР, которые строятся по передаточной функции (35).

ЛАЧХ определяется выражением:

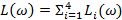
где ; ;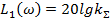

;

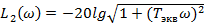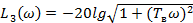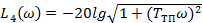
Фазовая характеристика определяется выражением:

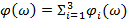
где ;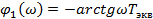

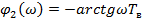
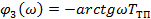
Замкнутая система устойчива, если фазовая характеристика разомкнутой системы не пересекает прямую φ(ω) = -π при L(ω)>0.

Критический коэффициент передачи системы

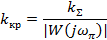
где 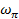- частота, при которой ЛФЧХ пересекает прямую φ(ω) = -π.