Интегральное исчисление. Неопределенный интеграл

Вопросы по теме

1. Неопределенный интеграл. Основные формулы интегрирования.

2. Непосредственное интегрирование. Интегрирование путём замены переменной. Интегрирование по частям.

3. Определенный интеграл.

Краткие теоретические сведения

Функция называется первообразной для функции в промежутке , если в любой точке этого промежутка ее производная равна : .

Отыскание первообразной функции по заданной ее производной или по дифференциалу есть действие обратное дифференцированию, интегрирование.

Совокупность первообразных для функции или дифференциала называется неопределенным интегралом и обозначается символом . Таким образом, , если .

Здесь - подынтегральная функция; - подынтегральное выражение; - произвольная постоянная.

Основные свойства неопределенного интеграла:

1.Неопределенный интеграл от дифференциала функции равен этой функции плюс произвольная постоянная:

.

2.Дифференциал неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции: .

3.Неопределенный интеграл алгебраической суммы функций равен алгебраической сумме неопределенных интегралов этих функций: .

4.Постоянный множитель подынтегрального выражения можно выносить за знак неопределенного интеграла:

5.Если и - любая известная функция, имеющая непрерывную производную, то .

Основные формулы интегрирования (таблица простейших интегралов):

1.   2.   3.   4.   5.   6.   7.   8.   9. 10. 11. 12.

13.   14.   15.   16. , 17. 18. 19. 20. 21. 22. 23. 24. .

Каждую из формул легко проверить. В результате дифференцирования правой части получается подынтегральное выражение.

Непосредственноеинтегрирование

Непосредственное интегрирование основано на прямом использовании таблицы интегралов. Здесь могут представиться следующие случаи:

1. данный интеграл находится непосредственно по соответствующему табличному интегралу;

2. данный интеграл после применения свойств 3 и 4 приводится к одному или нескольким табличным интегралам;

3. данный интеграл после элементарных тождественных преобразований над подынтегральной функцией и применения свойств 3 и 4 приводится к одному или нескольким табличным интегралам.

Примеры нахождения интегралов методом непосредственного интегрирования:

1. на основании свойства 4постоянный множитель 5 выносим за знак интеграла и используем формулу (1)

2. используем свойство 4 и формулу (1)

Проверка: . Получили подынтегральное выражение; следовательно, интеграл найден правильно.

3. используем свойства 3и 4 и формулу (1)

.

Постоянная интегрирования равна алгебраической сумме трех постоянных интегрирования, так как каждый интеграл имеет свою произвольную постоянную .

4. разложим квадрат разности и раскроем скобки

используем свойство 4 и формулу (1)

.

5. разделим каждый член числителя на знаменатель 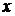, далее используя свойство 4 и формулу (1)получаем:

6. используем формулу (1)

7.

8. используем формулу (2)

9. так как , то .

10. так как , то Знак абсолютной величины не пишем, так как при любом значении 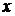выражение .

11. используем формулу (11) при получаем .

12. так как , то .

13. так как , то .

14. так как , то .

15. так как , то .

16. так как , то

.

17. .

18. так как , то следовательно .

19. .

20. так как , то

.

21. .

22. .

23. .

24. .

25.

Интегрирование методом замены переменной (метод подстановки)

Сущность интегрирования методом замены переменной (способом подстановки) заключается в преобразовании интеграла в интеграл , который легко вычисляется по какой-либо из основных формул интегрирования.

Для нахождения интеграла заменяем переменную 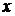новой переменной с помощью подстановки . Дифференцируя это равенство, получим . Подставляя в подынтегральное выражение вместо 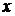и их значения, выраженные через и , имеем . После того как интеграл относительно новой переменной будет найден, с помощью подстановки он приводит к переменной .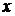

Примеры нахождения интегралов методом замены переменной (метод подстановки:

1.

введем подстановку . Дифференцируя, имеем , откуда . Подставив в данный интеграл вместо и их выражения, получим . Заменив его выражением через 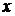, находим .

Проверка: .

2.

положим , откуда .

.

3. полагая , имеем . Значит,

.

4. положим , откуда . Поэтому, .

5. положим , откуда .

Следовательно, .

6. так как , то разделив и умножив знаменатель на ,

положим , тогда ,

т.е. . Таким образом, .

7. положим , тогда . Поэтому

.

8. положим , откуда . Значит .

9. положим , откуда .

Тогда получим .

10. положим , откуда . Следовательно, .

11. положим , откуда . Значит .

12. полагая , находим . Таким образом .

13. полагая , откуда . Таким образом .

Интегрирование по частям

Интегрируя обе части равенства , получим , откуда

(*)

С помощью этой формулы вычисление интеграла сводится к вычислению интеграла , если последний окажется проще исходного.

Примеры нахождения интегралов методом интегрирования по частям:

1. положим , тогда , т.е. . Получаем .

2. положим , тогда , . Получим .

3. положим , тогда .

в числителе подынтегральной функции последнего интеграла прибавим и вычтем и представим этот интеграл в виде суммы двух интегралов:

последний интеграл находим

.

перенеся из правой части в левую, получим

, или окончательно

.

Определенный интеграл

Пусть функция определена на отрезке . Разобьем этот отрезок на 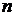частей точками , выберем на каждом элементарном отрезке произвольную точку и обозначим через длину каждого отрезка. Интегральной суммой для функции на отрезке называется сумма вида .

Определенным интегралом от функции на отрезке называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремиться к нулю .

Для любой функции , непрерывной на отрезке , всегда существует определенный интеграл .

Для вычисления определенного интеграла от функции в том случае, когда можно найти соответствующий неопределенный интеграл , служит формула Ньютона-Лейбница: , т.е. определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.

Непосредственное вычисление определенного интеграла

Примеры вычисления интегралов, используя формулу Ньютона-Лейбница:

1. ;

2. ;

3.

4. ;

5. ;

6. ;

7. ;

8. ;

9. .

Вычисление определенного интеграла методом замены переменной

При вычислении определенного интеграла методом замены переменной (способ подстановки) определенный интеграл преобразуется с помощью подстановки или в определенный интеграл относительно новой переменной . При этом старые пределы интегрирования и заменяются соответственно новыми пределами интегрирования и , которые находятся из исходной подстановки.

Из первой подстановки новые пределы интегрирования вычисляются непосредственно: , .

Из второй подстановки новые пределы интегрирования находятся путем решения уравнений и .

Таким образом, имеем .

Примеры вычисления интегралов:

1. Введем новую переменную интегрирования с помощью подстановки . Дифференцируя, имеем , откуда . Находим новые пределы интегрирования. Подставляя в соотношение значения и , соответственно получим . Следовательно

.

2. Положим , тогда . Вычисляем новые пределы интегрирования: . Таким образом

.

3. Положим , тогда . Вычисляем новые пределы интегрирования: . Поэтому

.

4. Преобразуем подкоренное выражение: . Положим , откуда . Найдем новые пределы интегрирования: . Следовательно,

Интегрирование по частям в определенном интеграле

Если функции и и их производные и непрерывны в промежутке , то формула интегрирования по частям для определенного интеграла имеет вид .

Пример вычисления интеграла:

1. Положим ; тогда . Следовательно, .