Кинематический анализ механизмов
2.1. Задачи и методы
Под кинематическим исследованием механизмов понимают изучение движений звеньев механизма без учета их масс и сил, действующих на эти звенья. Для выполнения кинематического исследования должны быть заданы схема и размеры механизма, а также законы движения его ведущих звеньев. В результате исследования по заданному закону движения ведущих звеньев определяются положения, угловые скорости и ускорения ведомых звеньев, а также перемещения, скорости и ускорения их отдельных точек (центров кинематических пар, центров масс и т. д). Рассмотрим вначале два простых движения твердого тела.
Поступательным движениемтвердого тела называется такое движение, при котором любая прямая, неизменно связанная с телом, перемещается параллельно самой себе, оставаясь параллельно своему начальному положению (рис.2.1).
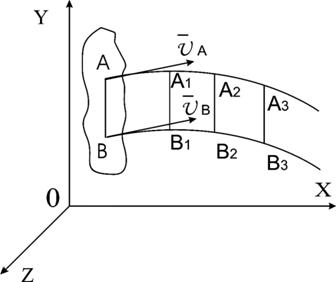
Рис.2.1. Поступательное движение
При поступательном движении все точки твердого тела описывают одинаковые траектории и в каждый момент имеют равные по модулю и направлению скорости и ускорения.
Если твердое тело движется так, что две какие-нибудь его точки остаются неподвижными, то такое движение называется вращательным. Неподвижная прямая, проходящая через две неподвижные точек, является осью вращения тела. Каждая точка, не лежащая на оси вращения, описывает при вращательном движении окружность, плоскость которой перпендикулярна оси вращения и центр которой лежит на этой оси (рис.2.2). Угол 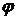 – угол поворота тела. Отсюда уравнение движения тела
– угол поворота тела. Отсюда уравнение движения тела 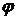 =f (t). Быстрота изменения угла поворота характеризуется угловой скоростью
=f (t). Быстрота изменения угла поворота характеризуется угловой скоростью 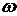 =
= 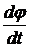 [1/c]. Переход от частоты вращения n (об/мин) к угловой скорости осуществляется по формуле:
[1/c]. Переход от частоты вращения n (об/мин) к угловой скорости осуществляется по формуле: 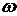 =
= 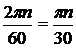 .
.
Когда угловая скорость тела постоянна ( 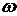 = const), вращение – равномерное. Угол поворота равен
= const), вращение – равномерное. Угол поворота равен 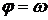 t. Перемещение т.М
t. Перемещение т.М 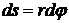 .(рис.2.2,а).
.(рис.2.2,а).
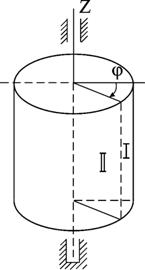
Рис.2.2. Вращательное движение
Линейная скорость т. М равна v = 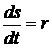
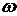 . Когда тело вращается неравномерно, то движение характеризуется угловым ускорением
. Когда тело вращается неравномерно, то движение характеризуется угловым ускорением
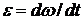 ,
,
т.е. первой производной угловой скорости по времени.
При ускоренном движении (рис.2.3,б) возникают касательное и нормальное ускорения соответственно равные
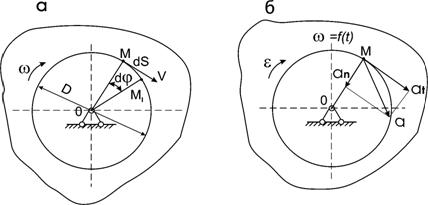 |
аt =
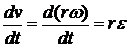 ; аn =
; аn = 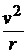 =
= 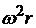 .
. Рис.2.3. Вращение тела: а – равномерное, б – неравномерное
Полное ускорение равно а = 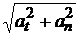 =
= 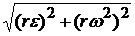 = r
= r 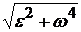 .
.
Направление полного ускорения определяется углом 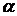
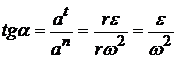 .
.
Плоскопараллельным (или плоским) движением твердого тела называется такое движение, при котором все точки тела движутся параллельно какой-нибудь неподвижной (основной плоскости) (рис.2.4, а). Всякое движение плоской фигуры в её плоскости можно рассматривать как совокупность поступательного движения, определяемого движением произвольно выбранного полюса, и вращательного движения вокруг этого полюса.
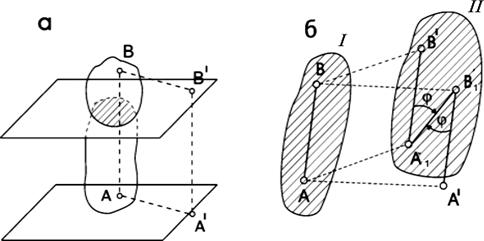
Рис.2.4. Плоскопараллельное движение
Рассмотрим перемещение плоской фигуры из положения I в положение II (рис.2.4,б). Определим положение фигуры отрезком АВ. Этот отрезок можно переместить из положения I в положение II. Перенеся его параллельно самому себе в положение А1В′ (фигура совершит поступательное перемещение), а  затем повернув отрезок вокруг точки А1 по часовой стрелки на угол φ (фигура совершит вращательное движение и займет положение II) так, чтобы точка В′ заняла свое положение В1. Можно также переместить фигуру поступательно из положения АВ в положение
затем повернув отрезок вокруг точки А1 по часовой стрелки на угол φ (фигура совершит вращательное движение и займет положение II) так, чтобы точка В′ заняла свое положение В1. Можно также переместить фигуру поступательно из положения АВ в положение 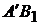 , а затем повернуть ее вокруг точки В1 на угол φ, чтобы точка
, а затем повернуть ее вокруг точки В1 на угол φ, чтобы точка 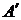 совпала с точкой А1.
совпала с точкой А1.
Поступательное перемещение зависит от выбора полюса, а величина угла поворота и направление поворота от выбора полюса не зависят.
Итак, плоскопараллельное движение можно разложить на два составляющих движения: поступательное вместе с некоторым полюсом т. М и вращательное вокруг этого полюса. Плоскопараллельное движение можно представить как сумму двух движений – поступательного и вращательного, то есть скорость любой точки тела равна геометрической (векторной) сумме скорости 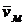 движения полюса (точка М) и скорости вращательного движения
движения полюса (точка М) и скорости вращательного движения 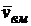 вокруг полюса М:
вокруг полюса М: 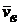 =
= 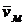 +
+ 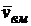 .
.
Скорость вращательного движения определяется по формуле
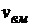 = ω
= ω 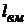 ,
,
где ω – угловая скорость вращения; 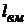 - радиус вращения точки В относительно полюса М. Скорость
- радиус вращения точки В относительно полюса М. Скорость 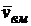 направлена перпендикулярно к радиусу вращения.
направлена перпендикулярно к радиусу вращения.
Из сказанного следует, что движение плоской фигуры в её плоскости будет определено, если для каждого момента времени известны значения функций
x =f1(t), y = f2(t) и φ = f3(t).
Примером плоскопараллельного движения является движение шатуна кривошипно-ползунного и четырехзвенного механизмов.
Основная задача кинематики в случае сложного движения состоит в том, чтобы, зная относительное и переносное движение точки, найти её абсолютное движение и определить траекторию, скорость и ускорение в этом движении.
Различают относительную, переносную и абсолютные скорости и ускорения точки. Абсолютная скорость 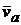 и абсолютное ускорение
и абсолютное ускорение 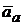 точки вызваны движением относительно неподвижной системы отсчета. Относительная скорость
точки вызваны движением относительно неподвижной системы отсчета. Относительная скорость 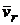 и относительное ускорение
и относительное ускорение 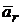 обусловлены движением по отношению к подвижной системе координат. Согласно теореме о сложении скоростей имеем, что абсолютная скорость точки равна геометрической сумме её переносной
обусловлены движением по отношению к подвижной системе координат. Согласно теореме о сложении скоростей имеем, что абсолютная скорость точки равна геометрической сумме её переносной 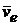 и относительной
и относительной 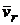 скоростей. Эту теорему называют правилом параллелограмма или треугольника скоростей. Абсолютное движение точки (или тела) можно назвать также сложным или результирующим движением, как результат сложения относительного и переносного движения.
скоростей. Эту теорему называют правилом параллелограмма или треугольника скоростей. Абсолютное движение точки (или тела) можно назвать также сложным или результирующим движением, как результат сложения относительного и переносного движения.
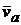 =
= 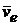 +
+ 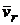 .
.
Абсолютное ускорение при переносном вращательном движении определяется зависимостью
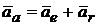 +2(
+2( 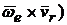
Здесь 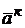 = 2(
= 2( 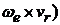 – поворотное ускорение точки (ускорение Кориолиса).
– поворотное ускорение точки (ускорение Кориолиса).
При поступательном переносном движении ускорение Кориолиса равно нулю и
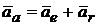 .
.
При плоском движении направление ускорения Кориолиса определяется поворотом вектора относительной скорости на 900 в направлении переносного вращения. Действительно, в общем случае три вектора 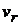 ,
, 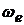 и
и 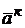 взаимно перпендикулярны. Если
взаимно перпендикулярны. Если 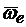 ^
^ 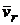 то sin(
то sin( 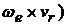 = 1, тогда
= 1, тогда
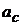 = 2
= 2 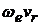 .
.
2.2. Свойства планов скоростей и ускорений
1.Векторы, выходящие из полюсов планов (скоростей и ускорений) соответствуют масштабным отрезкам абсолютных скоростей и ускорений
соответствующих точек. Концы этих векторов обозначаются в планах скоростей – а, в, с, в планах ускорений – 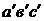 и носят название вершин планов.
и носят название вершин планов.
2.Отрезки, соединяющие вершины планов соответствуют относительным скоростям ( ускорениям.).
3.Одоименные отрезки и фигуры на схеме механизма и на планах скоростей (ускорений) пропорциональны, подобны и повернуты соответственно на углы 90° (план скоростей) и 180° – 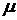 (план ускорений), где
(план ускорений), где 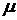 = arctg |
= arctg | 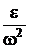 |.
|.
4.Точки, скорости (ускорения) которых равны нулю, располагаются в полюсе плана скоростей (ускорений).
2.3. Примеры построения планов положений
Покажем кинематическую схему заданного механизма в соответствии с заданными размерами и (начальным) углом 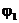 положения кривошипа. Принимаем масштабный коэффициент построения схемы механизма таким, чтобы она разместилась на отведенном поле чертежа. Следует учитывать расстояния между наиболее удаленными точками схемы механизма по вертикали и горизонтали. Построение планов скоростей и ускорений начинаем со звеньев, закон движения которых известен.
положения кривошипа. Принимаем масштабный коэффициент построения схемы механизма таким, чтобы она разместилась на отведенном поле чертежа. Следует учитывать расстояния между наиболее удаленными точками схемы механизма по вертикали и горизонтали. Построение планов скоростей и ускорений начинаем со звеньев, закон движения которых известен.
Пример 1
Схема поперечно-строгального станка (см. рис.1.4). Исходные данные: 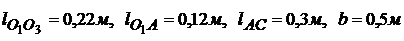 .
.
Масштаб построения будет определять размер b. Находим 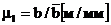 , где b – истинный (заданный) размер в м,
, где b – истинный (заданный) размер в м, 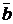 – выбранный масштабный отрезок в мм. Принимаем
– выбранный масштабный отрезок в мм. Принимаем 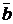 =100 мм. Получаем масштабный коэффициент плана положений
=100 мм. Получаем масштабный коэффициент плана положений 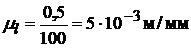 . Размеры остальных звеньев в мм равны
. Размеры остальных звеньев в мм равны
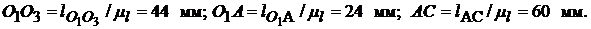
Изображаем в масштабе схему механизма (рис. 2.5).
Отмечаем положение неподвижных точек 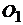 ,
, 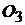 и направление движения ползуна 5. На окружности
и направление движения ползуна 5. На окружности 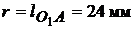 отмечаем точку А, определяемую заданным углом
отмечаем точку А, определяемую заданным углом 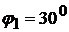 , отсчитываемым от горизонтального положения кривошипа. Находим положение точки С, отложив от точки А на продолжении прямой
, отсчитываемым от горизонтального положения кривошипа. Находим положение точки С, отложив от точки А на продолжении прямой 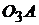 расстояние АС = 60 мм. Через точку С проводим вертикальную прямую до пересечения с линией хода ползуна (штока) и находим точку
расстояние АС = 60 мм. Через точку С проводим вертикальную прямую до пересечения с линией хода ползуна (штока) и находим точку 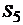 .
.
Пример 2
Схема брикетировочного автомата (рис. 1.6). Исходные данные:
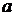 =0,23 м,
=0,23 м, 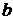 =0,41 м,
=0,41 м, 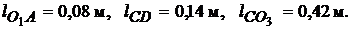
Находим масштабный коэффициент по наибольшему звену 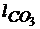 , принимая
, принимая 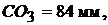 получим
получим 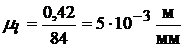 .
.
Определяем размеры других звеньев в масштабе:
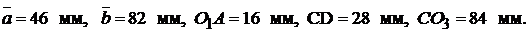
Отмечаем положение неподвижных точек О1, О3 (рис.2.8) и направление движения ползуна 5 параллельно оси О1Х. Проводим окружность радиусом О1А и находим на ней положение точки А в соответствии с заданным углом 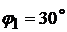 . Через точки О3 и А проводим прямую и находим положение точки С. Радиусом
. Через точки О3 и А проводим прямую и находим положение точки С. Радиусом 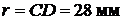 , из точки С делаем засечку на направлении движения ползуна 5 и получаем точку D.
, из точки С делаем засечку на направлении движения ползуна 5 и получаем точку D.
Пример 3
Схема компрессора (рис.1.11). Исходные данные:
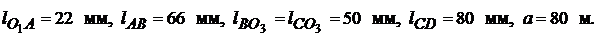
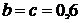 м. Находим
м. Находим 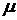 по размер
по размер 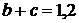 м.
м.
Получаем 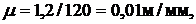 приняв
приняв 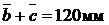 . Вычисляем
. Вычисляем 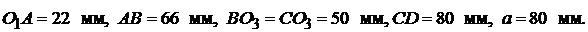 Выполняем построение схемы механизма. Отмечаем положение неподвижных точек О1, О3 и направление движения ползуна. Проводим окружность радиусом
Выполняем построение схемы механизма. Отмечаем положение неподвижных точек О1, О3 и направление движения ползуна. Проводим окружность радиусом 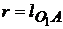 и находим точку А по углу
и находим точку А по углу 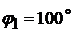 . Из точки О3 проводим дугу радиусом
. Из точки О3 проводим дугу радиусом 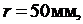 на которой из точки А радиусом r = 66 мм делаем засечку и определяем положение точки В. Затем строим равнобедренный треугольник О3ВС и из точки С радиусом r = 100 мм делаем засечку на направлении движения ползуна. Находим положение точки D.
на которой из точки А радиусом r = 66 мм делаем засечку и определяем положение точки В. Затем строим равнобедренный треугольник О3ВС и из точки С радиусом r = 100 мм делаем засечку на направлении движения ползуна. Находим положение точки D.
2.4.Примеры построения планов скоростей
Пример 1
Схема механизма, построенного описанным выше методом, показана на рис. 2.5, а соответствующий план скоростей изображен на рис. 2.6.
Пусть задано 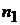 =100 об/мин, тогда угловая скорость кривошипа
=100 об/мин, тогда угловая скорость кривошипа 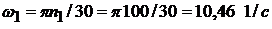 .
.
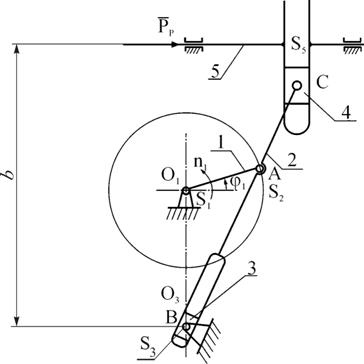
Рис. 2.5. Схема механизма
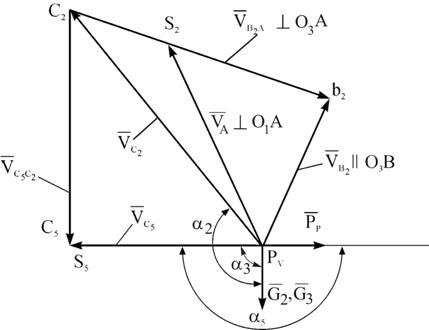
Рис. 2.6 План скоростей для поперечно-строгательного станка
Скорость точки А, принадлежащей одновременно первому и второму звену, 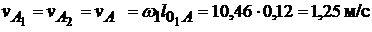 . Задаемся длиной вектора
. Задаемся длиной вектора 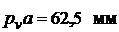 , тогда масштабный коэффициент плана скоростей равен
, тогда масштабный коэффициент плана скоростей равен 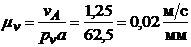 .
.
Рекомендуется принимать 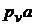 таким, чтобы
таким, чтобы 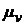 содержал одну значащую цифру: 1,2 и 5 с нулями, тогда все вычисления можно выполнять устно, не используя вычислительную технику. Из произвольно выбранной точки
содержал одну значащую цифру: 1,2 и 5 с нулями, тогда все вычисления можно выполнять устно, не используя вычислительную технику. Из произвольно выбранной точки 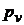 (полюса плана скоростей) проводим отрезок
(полюса плана скоростей) проводим отрезок 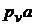 перпендикулярно положению кривошипа О1А в направлении угловой скорости (рис. 2.6). Для скорости точки В2 векторные уравнения имеют вид:
перпендикулярно положению кривошипа О1А в направлении угловой скорости (рис. 2.6). Для скорости точки В2 векторные уравнения имеют вид:
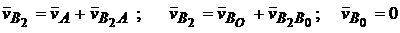
или 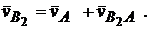
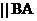
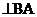
Здесь 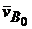 – скорость неподвижной точки,
– скорость неподвижной точки, 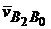 – скорость точки В2 относительно неподвижной точки В0, то есть скорость в абсолютном движении,
– скорость точки В2 относительно неподвижной точки В0, то есть скорость в абсолютном движении, 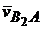 - скорость в относительном движении звена 2.
- скорость в относительном движении звена 2.
Решая последнее уравнение графически (через точку 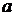 провести прямую, перпендикулярную звену ВС – направление вектора
провести прямую, перпендикулярную звену ВС – направление вектора 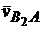 , а через точку
, а через точку 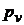 – прямую, параллельную звену ВС – направление вектора
– прямую, параллельную звену ВС – направление вектора 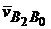 ), получим точку
), получим точку 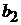 . Отрезок
. Отрезок 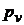
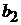 соответствует скорости
соответствует скорости 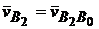 .
.
Скорость точки С можно определить, пользуясь свойством пропорциональности одноименных отрезков на плане положений механизма и на плане скоростей:
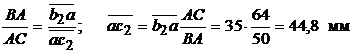
АС и АВ измеряемые на плане механизма, а 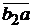 – на плане скоростей.
– на плане скоростей.
На продолжении отрезка 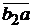 откладываем
откладываем 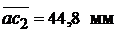 и получаем точку с2.
и получаем точку с2.
Для скорости точки С5 пятого звена векторные уравнения имеют вид:
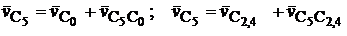
|| x || y
Решаем это уравнение графически. Из точки С2 проводим прямую, перпендикулярную направлению движения штока 5, а из полюса 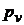 – прямую, параллельную собственному движению. Получаем точку
– прямую, параллельную собственному движению. Получаем точку 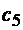 . Отрезок
. Отрезок 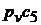 соответствует в масштабе
соответствует в масштабе 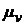 скорости точки С3. Скорости центров масс S2, S5 равны скоростям соответственно точек А и С5. Точки, скорости которых равны нулю, на плане скоростей находятся в полюсе
скорости точки С3. Скорости центров масс S2, S5 равны скоростям соответственно точек А и С5. Точки, скорости которых равны нулю, на плане скоростей находятся в полюсе 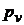 .
.
Определяем величины скоростей.
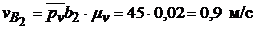 ;
;
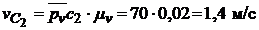 ;
; 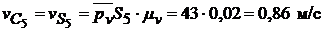 ;
; 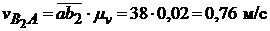 ,
,
где 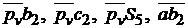 - отрезки в мм, снятые с плана скоростей.
- отрезки в мм, снятые с плана скоростей.
Находим угловую скорость звена 2:
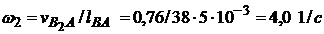 ,
,
которая направлена против часовой стрелки.
Примечание:Приведенные выше значения отрезков в мм при вычислении скоростей, могут изменится после размножении пособия.
Пример 2
Схема механизма брикетировочного автомата построена на рис. 2.7, а план скоростей и ускорений соответственно на рис. 2.8 и рис.2.12.
Задано: 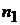 =40 об/мин. Угловая скорость кривошипа
=40 об/мин. Угловая скорость кривошипа
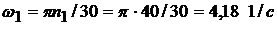 .
.
Построение планов начинаем с определения скоростей (ускорений) точек закон движения которых известен. Скорость точки А1,2, принадлежит одновременно 1 и 2 звену камню равна
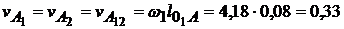 м/с
м/с
Задаемся длиной вектора 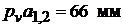 и вычисляем масштабный коэффициент плана скоростей:
и вычисляем масштабный коэффициент плана скоростей:
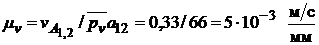 .
.
Из произвольно выбранной на чертеже точки 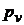 (полюс плана скоростей) проводим линию перпендикулярно положению кривошипа О1А (рис. 2.8) в направлении вращения кривошипа и откладываем на ней отрезок 66 мм. Составляем векторные уравнения для определения скоростей других точек. В абсолютном движении траектория т. А есть окружность радиуса
(полюс плана скоростей) проводим линию перпендикулярно положению кривошипа О1А (рис. 2.8) в направлении вращения кривошипа и откладываем на ней отрезок 66 мм. Составляем векторные уравнения для определения скоростей других точек. В абсолютном движении траектория т. А есть окружность радиуса 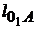 и может быть получена сложением переносного (вращение кулисы 3) и относительного (перемещения ползуна 2 вдоль кулисы движений (рис.2.9). На рисунке дуга АА` – траектория абсолютного движения, дуга АА′ при вращении кулисы – траектория переносного движения, перемещение по прямой А′А′′ вдоль кулисы – относительное движение. Таким образом, из точки А в абсолютном движении попадаем в точку А′′ выполняя два движения: поворачивая кулису и перемещая ползун вдоль неё.
и может быть получена сложением переносного (вращение кулисы 3) и относительного (перемещения ползуна 2 вдоль кулисы движений (рис.2.9). На рисунке дуга АА` – траектория абсолютного движения, дуга АА′ при вращении кулисы – траектория переносного движения, перемещение по прямой А′А′′ вдоль кулисы – относительное движение. Таким образом, из точки А в абсолютном движении попадаем в точку А′′ выполняя два движения: поворачивая кулису и перемещая ползун вдоль неё.
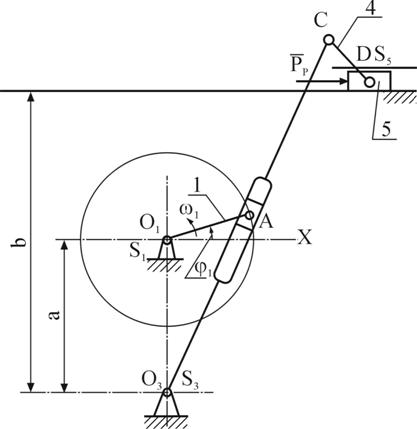
Рис. 2.7. Схема механизма брикетировочного автомата
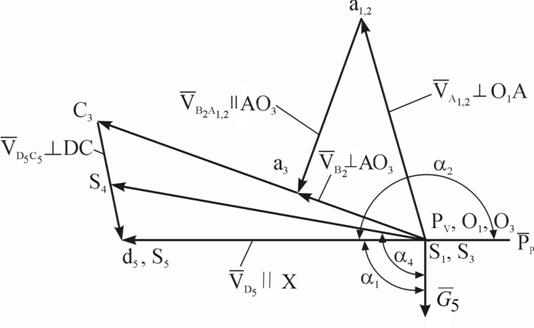
Рис. 2.8 План скоростей механизма брикетировочного автомата
Запишем уравнения
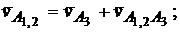
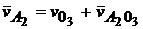 ;
; 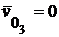 .
.
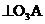
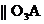
Здесь 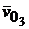 – скорость неподвижной точки, равная нулю;
– скорость неподвижной точки, равная нулю; 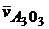 – скорость точки A3 относительно О3;
– скорость точки A3 относительно О3; 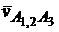 – скорость точки A1,2 в относительном движении по отношению к А3.
– скорость точки A1,2 в относительном движении по отношению к А3.
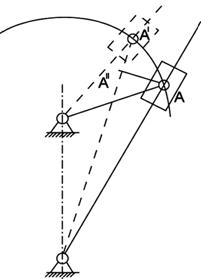
Рис.2.9. Сложение движений
Векторные уравнения решаем графически (рис. 2.8) Через полюс 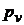 проводим направление
проводим направление 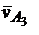 перпендикулярно AО3, а через конец вектора
перпендикулярно AО3, а через конец вектора 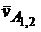 проводим прямую, параллельную AО3. Пересечение определяет положение точки a3 – конец вектора
проводим прямую, параллельную AО3. Пересечение определяет положение точки a3 – конец вектора 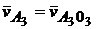 . Скорость точки С можно определить, используя свойство пропорциональности одноименных отрезков,
. Скорость точки С можно определить, используя свойство пропорциональности одноименных отрезков,
а именно: 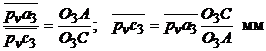 .
.
Откладываем на продолжение 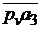 отрезок
отрезок 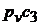 и находим точку
и находим точку 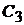 .
.
Для скорости точки D векторное уравнение имеет вид
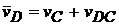 ;
; 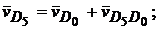
|| X 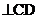
Решаем это уравнение графически (рис. 2.8). Через полюс рv проводим направление скорости параллельно оси Х. Через точку c3 проводим направление относительной скорости 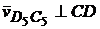 . Пересечение этих прямых дает точку d, с которой будет совпадать точка s5, а точка s4 по свойству пропорциональности лежит на середине вектора относительной скорости
. Пересечение этих прямых дает точку d, с которой будет совпадать точка s5, а точка s4 по свойству пропорциональности лежит на середине вектора относительной скорости 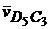 . Точки, скорость которых равна нулю, на плане скоростей находятся в полюсе
. Точки, скорость которых равна нулю, на плане скоростей находятся в полюсе 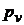 .
.
Определяем величины линейных скоростей точек звеньев механизма:
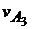 =
= 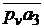 ∙μv = 26∙0,005 = 0,13 м/с;
∙μv = 26∙0,005 = 0,13 м/с;
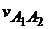 =
= 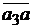 μv =36∙0,005 = 0,18 м/с;
μv =36∙0,005 = 0,18 м/с;
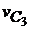 =
= 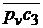 ∙μv = 67∙0,005 = 0,335 м/с;
∙μv = 67∙0,005 = 0,335 м/с;
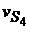 =
= 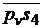 ∙μv = 62∙0,005 = 0,31 м/с;
∙μv = 62∙0,005 = 0,31 м/с;
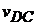 =
= 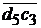 μv = 23∙0,005 = 0,115 м/с;
μv = 23∙0,005 = 0,115 м/с;
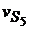 =
= 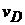 =
= 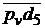 μv = 58∙0,005 = 0,29 м/с.
μv = 58∙0,005 = 0,29 м/с.
и угловых скоростей:
ω3 = 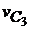 /
/ 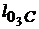 = 0,335/0,42 = 0,798 1/с;
= 0,335/0,42 = 0,798 1/с;
ω4 = 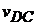 /lDC = 8,58/0,14 = 0,821 1/с.
/lDC = 8,58/0,14 = 0,821 1/с.
Пример 3
Схема механизма компрессора показана на рис. 2.10, а план скоростей изображен на рис. 2.11.
Задано: 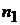 =60 об/мин. Угловая скорость
=60 об/мин. Угловая скорость
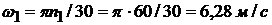 .
.
Скорость точки А, принадлежащей звеньям 1,2:
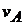 =
= 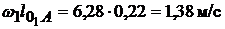 .
.
Задаемся длиной вектора 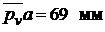 и находим
и находим
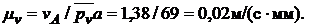
Из выбранной точки 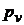 (полюс плана скоростей) проводим отрезок перпендикулярно положению кривошипа О1А (рис. 2.11) в направлении
(полюс плана скоростей) проводим отрезок перпендикулярно положению кривошипа О1А (рис. 2.11) в направлении 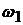 . Для точки В, принадлежащей одновременно двум звеньям 2 и 3, векторное уравнение запишем:
. Для точки В, принадлежащей одновременно двум звеньям 2 и 3, векторное уравнение запишем:
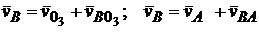
или 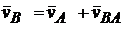
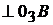
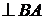
Решаем это уравнение графически (рис. 2.13). Через точку 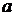 проводим прямую, перпендикулярную звену АВ, а из полюса – прямую, перпендикулярную О3В. Пересечение прямых определяет положение точки
проводим прямую, перпендикулярную звену АВ, а из полюса – прямую, перпендикулярную О3В. Пересечение прямых определяет положение точки 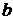 . Точка с принадлежит 3-ему звену (треугольник ВО3С). Такой же треугольник (подобный) построим на плане скоростей
. Точка с принадлежит 3-ему звену (треугольник ВО3С). Такой же треугольник (подобный) построим на плане скоростей 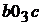 . Векторные уравнения для определения скорости точки D будут
. Векторные уравнения для определения скорости точки D будут
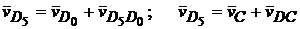 ,
, 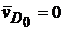 или
или
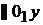
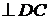
Из точки c проводим прямую, перпендикулярную DC, а через полюс – прямую, параллельную оси у. Пересечение определяет точку d. Скорости центров масс S2, S4 находим по свойству пропорциональности. Концы векторов расположены в середине векторов. Точки, скорости которых равны нулю, находятся в полюсе. Скорости точек и угловые скорости звеньев определяем аналогично 2-му примеру.
Рис. 2.10. Схема механизма
Рис. 2.11. План скоростей
2.5. Примеры построения планов ускорений
Построение плана ускорений рассмотрим на примере брикетировочного автомата (схемы кулисного механизма) и компрессора (механизм без кулисных пар).
Брикетировочный автомат(рис. 2.7). Точка А одновременно принадлежит звеньям 1,2 и 3. Ускорение точки 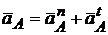 . Начальное звено (1) – кривошип вращается с постоянной угловой скоростью, поэтому составляющая
. Начальное звено (1) – кривошип вращается с постоянной угловой скоростью, поэтому составляющая 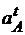 = 0, и
= 0, и 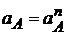
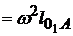 = 4,182∙0,08 = 1,4 м/с2. Масштабный коэффициент плана ускорений
= 4,182∙0,08 = 1,4 м/с2. Масштабный коэффициент плана ускорений 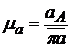 . Задаем
. Задаем 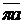 = 70 мм, тогда
= 70 мм, тогда
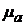 =
= 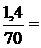 0,02 (м/с2 )/ мм.
0,02 (м/с2 )/ мм.
Из произвольно выбранной точки на чертеже (π – полюс плана) откладываем нормальную составляющую 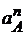

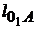 в виде 70 мм, направленную к центру вращения кривошипа 01 (рис.2.12). Составляем векторные уравнения для определения ускорений других точек. Ускорения точки А, принадлежащей первому и второму звену (камню) будут равны
в виде 70 мм, направленную к центру вращения кривошипа 01 (рис.2.12). Составляем векторные уравнения для определения ускорений других точек. Ускорения точки А, принадлежащей первому и второму звену (камню) будут равны 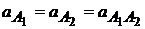 .
.
Поскольку переносное движение вращательное, имеем следующее векторное уравнение
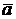
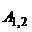 =
= 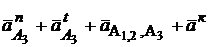 , ( * )
, ( * )
где 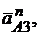
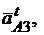 – соответственно нормальная и тангенциальная составляющие переносного движения для точки
– соответственно нормальная и тангенциальная составляющие переносного движения для точки 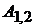 , которое является абсолютным для точки
, которое является абсолютным для точки 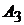 (рис.2.10). Ускорение
(рис.2.10). Ускорение 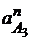 =
= 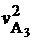 /
/ 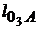 , а
, а 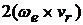 =
= 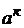
– поворотное ускорение точки 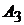 (ускорение Кориолиса). Угловая скорость переносного движения
(ускорение Кориолиса). Угловая скорость переносного движения 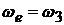 , а относительная скорость
, а относительная скорость 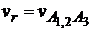 . Направление вектора
. Направление вектора 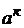 можно определить, если
можно определить, если 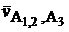 повернуть на 900 по направлению угловой скорости
повернуть на 900 по направлению угловой скорости 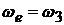 .
.
Согласно уравнению (*) строим вектор 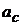 , перпендикулярно положению кулисы О3А и входящим в конец вектора
, перпендикулярно положению кулисы О3А и входящим в конец вектора 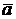
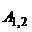 .. Через начало вектора
.. Через начало вектора 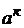 проводим направление
проводим направление 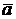
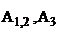 ||О3А. Далее из полюса
||О3А. Далее из полюса 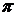 проводим вектор
проводим вектор 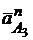 || О3А в направлении к т.О3, а из его конца направление вектора
|| О3А в направлении к т.О3, а из его конца направление вектора 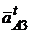
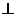 О3А до пересечения с направлением
О3А до пересечения с направлением 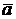
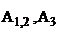 . Пересечение определяет положение точки
. Пересечение определяет положение точки 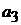 .
.
Положение точки 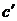 на плане ускорений находим, как и при построении плана скоростей, по свойству подобия из условия
на плане ускорений находим, как и при построении плана скоростей, по свойству подобия из условия
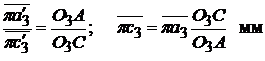 .
. 
Для определения вектора ускорения точки 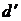 запишем уравнения:
запишем уравнения:
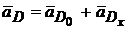 ;
; 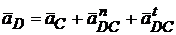 .
.
|| xx || DC 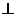 DC
DC
Здесь 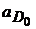 = 0. Решаем последние векторные уравнения. Из точки с′
= 0. Решаем последние векторные уравнения. Из точки с′
проводим величину вектора 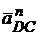 || DC. Конец вектора обозначим через n′ и через эту точку проводим направление
|| DC. Конец вектора обозначим через n′ и через эту точку проводим направление 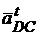
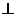 DC до пересечения с направлением xx. Получаем точку
DC до пересечения с направлением xx. Получаем точку 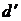 конец вектора
конец вектора 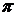
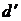
 Модуль вектора
Модуль вектора
׀ 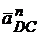 ׀ =
׀ = 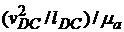 в мм.
в мм.
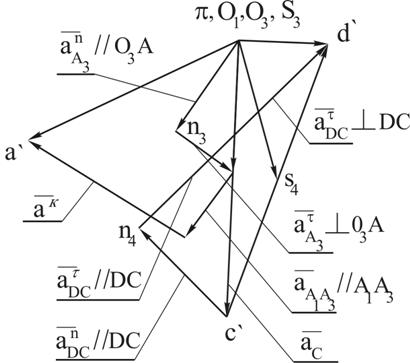
Рис.2.12. План ускорений механизма брикетировочного автомата
Рассмотрим построение плана ускорений для механизма компрессора (рис.2.10).
Начинаем с вычисления ускорения точки А, принадлежащей одновременно звеньям 1,2.
Для принятых исходных данных 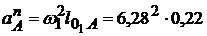 =8,7 м/с2. Выбираем
=8,7 м/с2. Выбираем 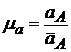 . Задаем
. Задаем 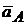 = 87 мм, т.е.
= 87 мм, т.е. 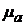 = 0,1 (м/с2 )/ мм.
= 0,1 (м/с2 )/ мм.
Из произвольно выбранной точки на чертеже (π – полюс плана) откладываем нормальную составляющую 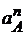

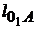 величиной 87 мм, направленную к центру вращения кривошипа 01 (рис.2.13). Конец вектора обозначим
величиной 87 мм, направленную к центру вращения кривошипа 01 (рис.2.13). Конец вектора обозначим 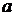 . Составляем векторные уравнения для определения ускорений других точек. Ускорения точки А, принадлежащей первому и второму звену (камню) будут равны
. Составляем векторные уравнения для определения ускорений других точек. Ускорения точки А, принадлежащей первому и второму звену (камню) будут равны 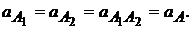
Для определения ускорения точки В запишем векторные уравнения движения этой точки относительно 03 и относительно точки А. Имеем
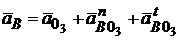 ;
; 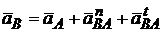 .
.
Используя план скоростей (рис.2.10), вычисляем составляющие:
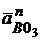 =
= 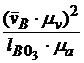 мм, или
мм, или 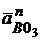 =
= 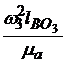 мм. Аналогично
мм. Аналогично 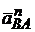 =
= 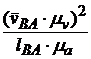 мм. Находим положение конца вектора
мм. Находим положение конца вектора 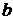 на плане ускорений. Из полюса π проводим вектор
на плане ускорений. Из полюса π проводим вектор 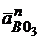 || О3В (конец вектора обозначаем n1) и через него направление вектора
|| О3В (конец вектора обозначаем n1) и через него направление вектора 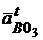
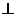 О3В. Далее из конца вектора
О3В. Далее из конца вектора 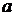 строим вектор
строим вектор 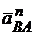 ||АВ (конец вектора
||АВ (конец вектора 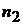 ) и через его конец проводим направление вектора
) и через его конец проводим направление вектора 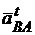
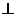 ВА до пересечения с направлением вектора
ВА до пересечения с направлением вектора 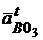 . Точка пересечения и будет точка
. Точка пересечения и будет точка 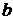 конец вектора
конец вектора 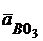 =
= 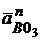 +
+ 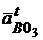 . Вектор
. Вектор 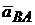 =
= 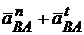 избражен отрезком на плане ускорений
избражен отрезком на плане ускорений  , в середине которого располагается точка
, в середине которого располагается точка 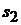 , конец вектора укорения центра масс шатуна. Положение точки
, конец вектора укорения центра масс шатуна. Положение точки 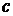 находим, используя свойство подобия. Треугольник ВО3С на плане положений механизма должен быть подобен и сходственно расположен соответствующему треугольнику на плане ускорений
находим, используя свойство подобия. Треугольник ВО3С на плане положений механизма должен быть подобен и сходственно расположен соответствующему треугольнику на плане ускорений 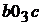 .
.
Запишем векторные ускорения для определения ускорения точки D, имеем
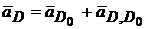 и
и 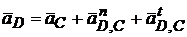 . Величина вектора
. Величина вектора 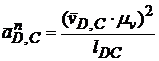 мм.
мм. 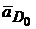 = 0, а вектор
= 0, а вектор 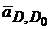 представляет ускорение вдоль направляющих, т.е. абсолютное ускорение точки D,
представляет ускорение вдоль направляющих, т.е. абсолютное ускорение точки D, 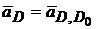
Проводим через полюс 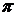 вертикальную прямую, направление вектора
вертикальную прямую, направление вектора 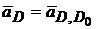 . Из конца вектора
. Из конца вектора 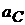 , точки
, точки 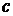 проводим величину вектора
проводим величину вектора
