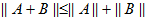Сформулируйте каноническое уравнение мнимого эллипса.
Если же в правой части стоит единица со знаком минус, то получившееся уравнение:
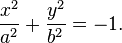 описывает мнимый эллипс. Изобразить такой эллипс в действительной плоскости невозможно.
описывает мнимый эллипс. Изобразить такой эллипс в действительной плоскости невозможно.
36.Гипербола – геометрическое место точки плоскости, для которых разность расстояния до фиксированных точекF1 иF2 есть постоянная величина 2a
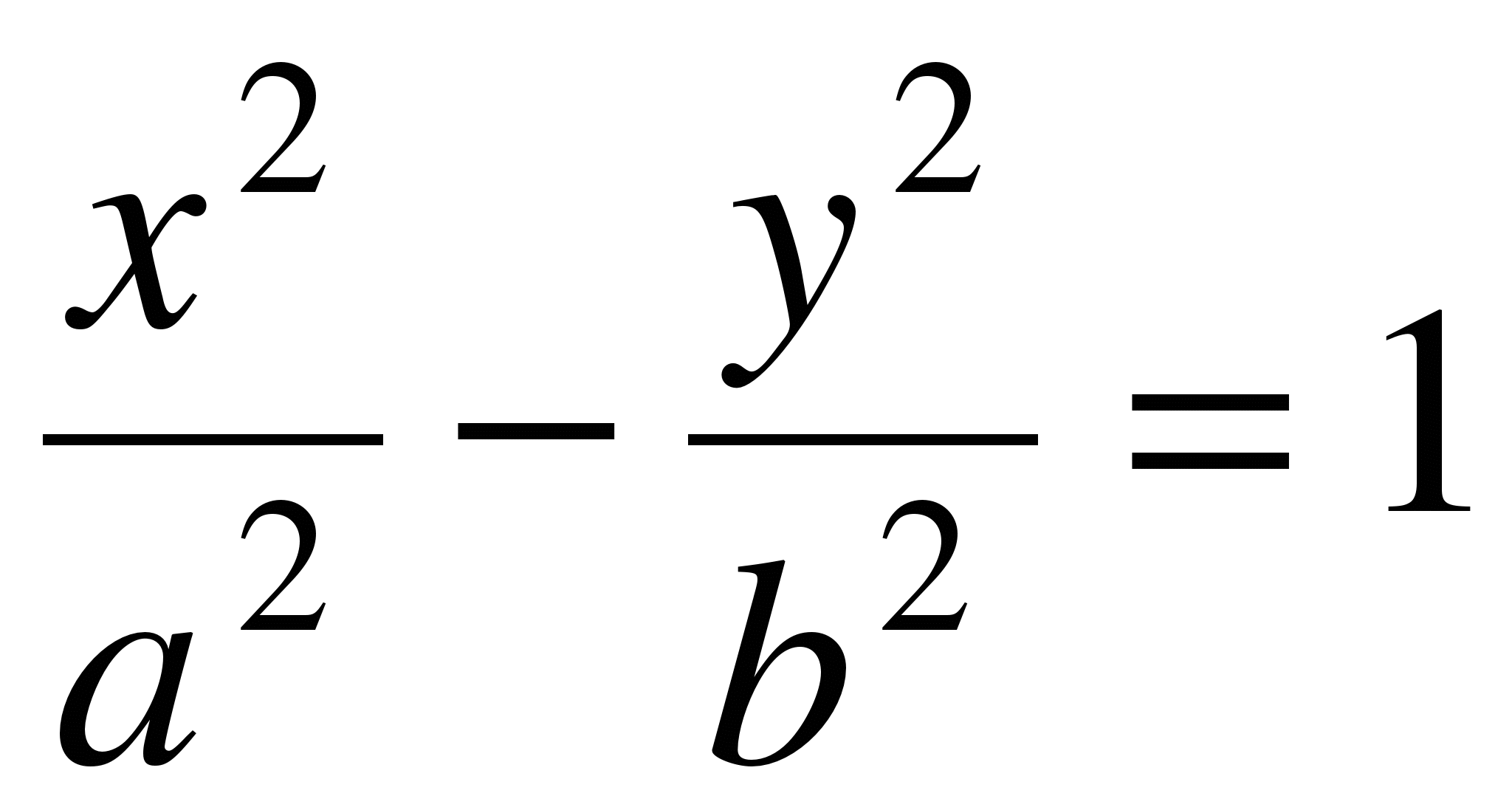
37. Парабола – геометрическое место точки плоскости, равноудаленное от фиксированной точки F(фокуса) и от фиксированной прямой (директрисы).
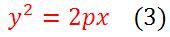
39. 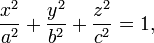
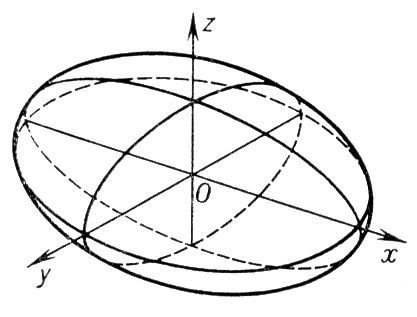
40. 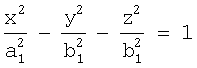
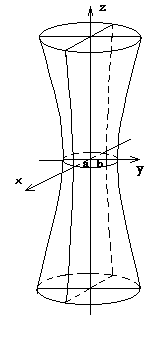
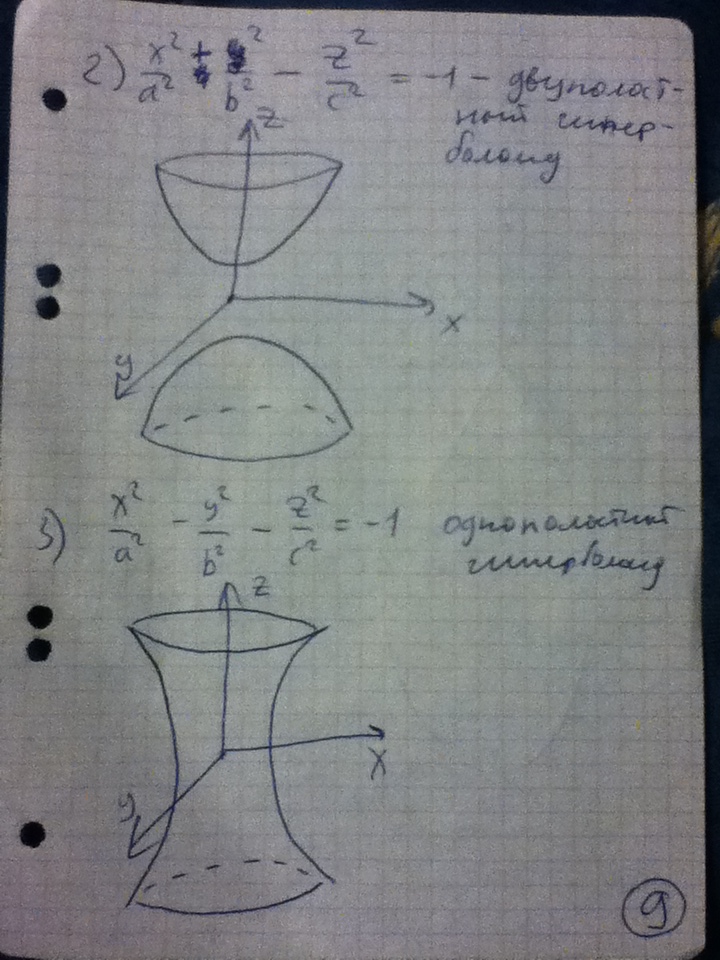
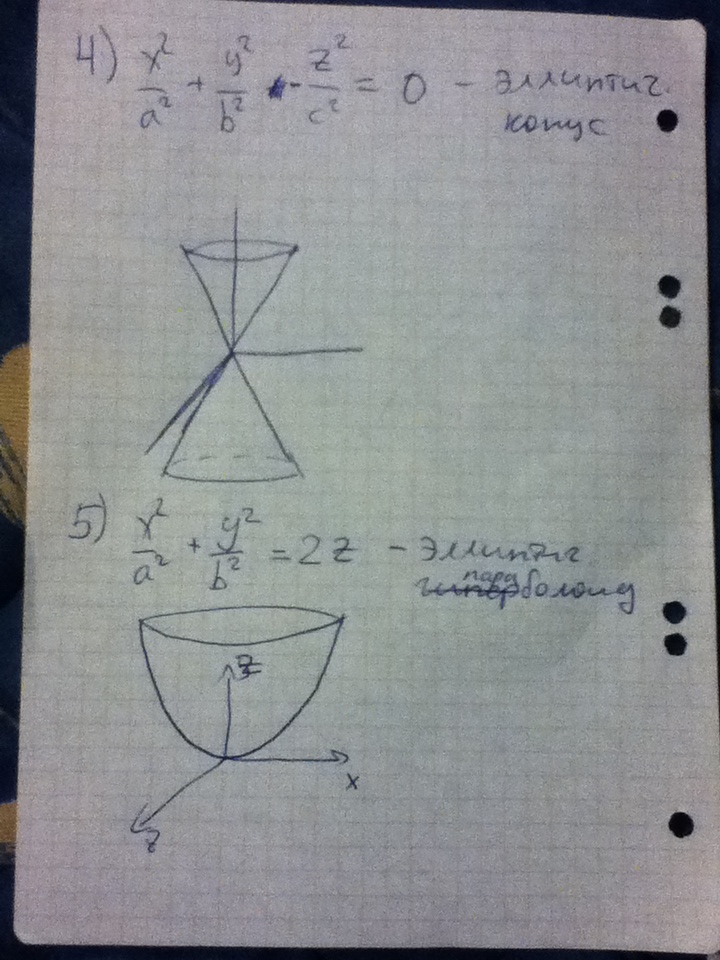

46. Гиперболический цилиндр — поверхность второго порядка, направляющей для которой служит гипербола. Гиперболический цилиндр образуется при перемещении гиперболы по прямой. Это линейчатая поверхность. Каноническое уравнение гиперболического цилиндра следующее:
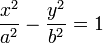
Гиперболический цилиндр может быть обозначен параметрически:
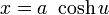
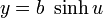
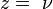
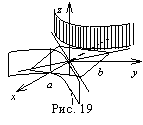
47.Параболический цилиндр — цилиндрическая поверхностьвторого порядка, для которой образующей служит парабола. Ее получают при перемещении параболы по направляющей прямой. Тогда следом от параболы будет параболический цилиндр.
Каноническое уравнение:
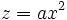 ,
,
При 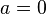 вырождается в плоскость.
вырождается в плоскость.
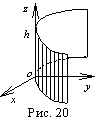
48. Пара пересекающихся плоскостей:
X2/a2 – y2/b2 = 0 (пара действительных пересекающихся плоскостей)
a>0, b>0, где 1/a2 + 1/ b2 =1
х2/a2 + y2/b2 = 0 ( пара мнимых пересекающихся плоскостей)
a >0, b >0, где 1/a2 + 1/ b2 =1
Пара действиетельных параллельных плоскостей задаётся уравнением:
y2–b2= 0, b >0.
Пара мнимых параллельных плоскостей задаётся уравнением:
y2+ b2= 0, b >0.
Наконец, пара совпадающих плоскостей задаётся уравнением:
y2= 0.
49.
Для любых чисел 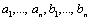
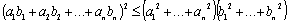 .
.
Доказательство
При 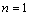 неравенство
неравенство 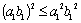 верно. Допустим,
верно. Допустим,
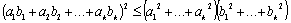 .
.
Докажем, что
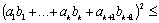
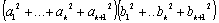 .
.
Перепишем это неравенство, частично раскрыв скобки:
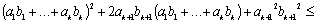
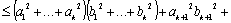
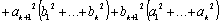 .
.
Легко заметить, что для того, чтобы доказать это неравенство, достаточно доказать
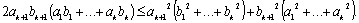
Перенеся все слагаемые в одну сторону, и сгруппировав их, получаем очевидное неравенство:
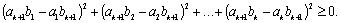
А это и доказывает неравенство Коши-Буняковского.
Определение 2
1. Число 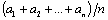 называется средним арифметическим чисел
называется средним арифметическим чисел 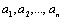 .
.
2. Если 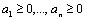 , то число
, то число 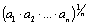 называется средним геометрическим чисел
называется средним геометрическим чисел 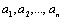 .
.
Теорема 3 (неравенство Коши)
Пусть 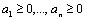 , тогда
, тогда
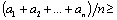
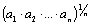 . (1)
. (1)
Доказательство
Шаг первый: сначала индукцией докажем это неравенство для натуральных чисел вида 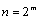 . При m=1 надо доказать, что
. При m=1 надо доказать, что 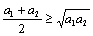 . Это неравенство эквивалентно
. Это неравенство эквивалентно 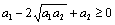 , то есть
, то есть 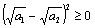 . Последнее неравенство верно, значит, и первоначальное верно, так как они равносильны. Допустим, неравенство верно при m=k, то есть
. Последнее неравенство верно, значит, и первоначальное верно, так как они равносильны. Допустим, неравенство верно при m=k, то есть
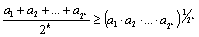 . (2)
. (2)
Докажем неравенство (1) для m=k+1, то есть докажем, что
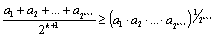 .
.
В самом деле, 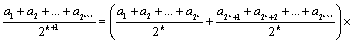
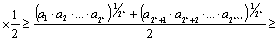
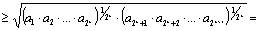
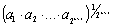 .
.
Итак, мы доказали неравенство Коши, когда количество чисел в средних есть степень двойки. А как быть с остальными? Для них мы докажем неравенство Коши, используя еще одну модификацию индукции – "индукцию вниз". Допустим, что неравенство Коши верно для n=k, то есть допустим, что
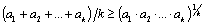 , (3)
, (3)
и докажем это неравенство для n=k-1. Для этого в неравенстве Коши положим 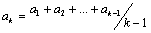 , тогда (3) будет иметь вид:
, тогда (3) будет иметь вид:
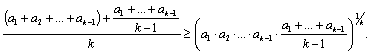
После элементарных алгебраических преобразований получили:
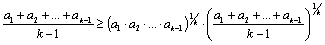 .
.
Сократим неравенство на второй множитель правой части:
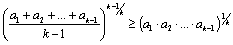 .
.
И, наконец, возведем обе части неравенства в степень 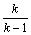 :
:
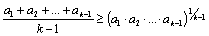 .
.
Неравенство Коши доказано полностью.
50.Доказательство неравенства треугольника равносильно проверке неравенства
|
для произвольных операторов A, BÎ 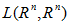 . Докажем это неравенство. Пусть
. Докажем это неравенство. Пусть
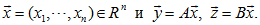 |
Мы имеем:
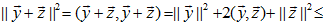 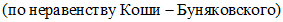 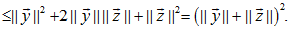 |
Таким образом, для каждого 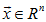 справедливо неравенство
справедливо неравенство
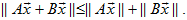 |
Доказано.
56. Докажите теорему о пространстве решений однородной системы линейных алгебраических уравнений
Совокупность P всех решений однородной системы уравнений является линейным пространством, которое представляет собой подпространство линейного пространства всех вектор-столбцов высоты n.
Пусть имеется однородная система линейных уравнений, которую можно записать в матричном виде Ax=0 , где A - матрица системы, а x- столбец неизвестных. Известно, что столбцы-решения системы можно складывать и умножать на число. При этом будут получаться снова решения этой системы. Значит, на множестве решений определены операции сложения и умножения на число. Легко проверить, что эти операции удовлетворяют требованиям из определения линейного пространства. Итак, множество решений однородной системы линейных уравнений является линейным пространством.
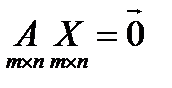
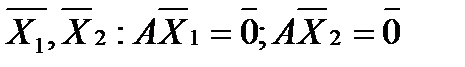
1). 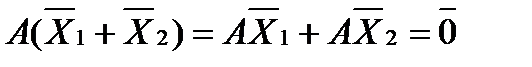
2). 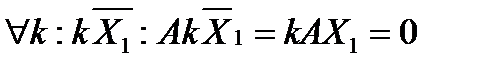
57. Докажите теорему о связи общих решений неоднородной и однородной систем линейных алгебраических выражений
Система вида: 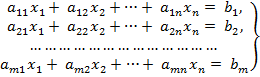 называется системой линейных алгебраических уравнений. Данная система является однородной, если все bi, i=1,2,…,m равны нулю. В противном случае, т.е. при b≠0, система называется неоднородной.
называется системой линейных алгебраических уравнений. Данная система является однородной, если все bi, i=1,2,…,m равны нулю. В противном случае, т.е. при b≠0, система называется неоднородной.
Общее решение неоднородной системы представляет собой сумму общего решения соответствующей однородной системы и частного решения системы.
Итак, общее решение неоднородной системы линейных уравнений имеет вид : 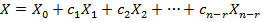 , где Х0 - некоторое (частное) решение неоднородной системы уравнений.
, где Х0 - некоторое (частное) решение неоднородной системы уравнений.
Общее решение однородной системы: 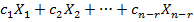
Также систему неоднородных уравнений можно записать в матричном виде Ax=b , где матрица A имеет размеры mxn .
Пусть c и d -- решения неоднородной системы Ax=b. Тогда их разность g=c – dявляется решением однородной системы с той же матрицей, то есть решением системы Ax=0 .
Доказательство. По условию Ac=b и Ad=b . ТогдаAg=A(c-d)=Ac – Ad = b – b = 0
Так как Ag=0 , то g -- решение однородной системы.
58. Выведите формулы Крамера для системы двух линейных уравнений с двумя переменными
Квадратной матрицей второго порядка называется совокупность из четырех чисел, записанных в таблице 2 х 2: 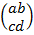 . Число ad - bc называется определителем такой матрицы, и обозначается
. Число ad - bc называется определителем такой матрицы, и обозначается 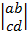 . Если x =
. Если x = 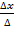 , то y=
, то y= 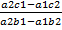 . Аналогично получаем, что x=
. Аналогично получаем, что x= 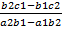 .
.
Как легко заметить, величины 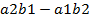 ,
, 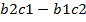 ,
, 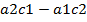 являются определителями матриц соответственно
являются определителями матриц соответственно 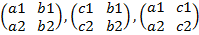 . Отсюда следует правило Крамера: Система линейных уравнений:
. Отсюда следует правило Крамера: Система линейных уравнений: 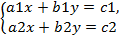 имеет единственное решение тогда и только тогда, когда ∆≠0, и находится по формуламx =
имеет единственное решение тогда и только тогда, когда ∆≠0, и находится по формуламx = 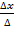 , y=
, y= 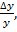 где∆=
где∆= 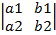 , ∆x =
, ∆x = 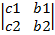 , ∆y=
, ∆y= 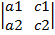
59. Докажите, что вектора ортонормированной системы векторов линейно независимы
Ортогональная система векторов в Enназывается ортонормированной, если длина любого вектора равна единице.
Всякая ортонормированная система векторов линейно независима. Докажем эту теорему.
Пусть a1 , a2 , ….. as – ортонормированная система векторов. Рассмотрим их линейную комбинацию и приравняем к нулю:a1 a1 +a2a2 + …+ asas= 0
Умножимобечастискалярнонаai:a1 (a1,ai) +a2 (a2,ai)+ … + as (as,ai)= 0
Учитывая, что: (ai , aj) = 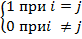 , получаем равенство αi= (0, ai)
, получаем равенство αi= (0, ai)
Из следующей цепочки равенств: (0,a) = (b – b,a) = (b,a) + (-b,a) = (b,a) – (b,a) = 0, заключаем, что (0,ai) = 0, а потому все αiравны нулю, т.е. ортонормированная система линейно независима.
60. Выведите формулы для вычисления координат вектора в ортогональном базисе
Известно, что n векторов e1, e2, …., en , ни один из которых не равен нулю, образуют ортогональный базис в n-мерном евклидовом пространствеR, если они попарно ортогональны, т.е. (ei , ej) = 0 приiне равном j.
Кроме того, векторыe1, e2, …., en образуют ортогональный нормированный базис, если они попарно ортогональны и имеют каждый длину 1.
Найдем координаты вектора x в нормированном ортогональном базисе e1, e2, …., en.
Пусть x = ξ1e1 + ξ2e2 +… +ξnen
Умножив обе части этого равенства скалярно на e1, получим:
(x, e1) = ξ1 (e1 , e1) + ξ2 (e2 , e1)+… +ξn(en , e1) = ξ1
И, аналогично,
ξ2 = (x, e2), ………….. , ξn= (x, en)
Итак, координаты вектора в ортогональном нормированном базисе есть скалярные произведения этого вектора на соответствующие базисные векторы.
62.Пусть системы векторов e = {e1, ..., en} и f = {f1, ..., fn} — два базиса n-мерного линейного пространства Ln.
Обозначим xe = (x1,x2, ..., xn) и xf = (x'1,x'2, ..., x'n) — координаты вектора x ∈ Ln соответственно в базисах e и f.
Справедливо следующее xe= Ce→f·xf :
Здесь Ce→f — матрица перехода от базиса e к базису f, это матрица, столбцами которой являются координаты базисных векторов f1, ..., fn в базисе e1, ..., en:
f1 = с11· e2 + с21· e1 + ... + сn1· en, f2 = с12· e1 + с22· e2 + ... + сn2· en, ..., fn = с1n· e2 + ... + сnn· en.
Формулу преобразования координат вектора при изменении базиса принято записывать в виде:
xf= (Ce→f)− 1·xe
63. Преобразование матрицы линейного оператора при изменении базиса: пусть – фи лин оператор с матрицей А в базисе е .
Если e'=Te , то A'=TA*1/T
64.Обозначим характеристические многочлены: PA(λ) = det (A − λE), PB(λ) = det (B − λE); нам дано, что A ~ B, т.е. B = C−1AC. Имеем: PB(λ) = det (B − λE) = det (C−1AC − C−1(λE)C) = det (C−1(A − λE)C) = detC−1×det (A − λE)×detC = det (A − λE) = PA(λ), чтоитребовалосьдоказать.
Спектры подобных матриц совпадают.
Из этой теоремы следует, что можно ввести понятия характеристического многочлена Pφ (λ), характеристического уравнения и спектра Sφ оператора j, вычисляя их по матрице Aj, взятой в произвольном базисе пространства V.
65.Рассмотрим самосопряженный операторА и два его собственных вектора х1 и х2, отвечающие различным собственным значениям λ1 и λ2. Тогда Ах1 = λ1х1 и Ах2 = λ1х2.
Поэтому (Ах1, х2) = (λ1х1, х2) = λ1(х1,х2) (1)
Но так какА является самосопряженным оператором, то (Ах1, х2) = (х1, Ах2). Значит,
(Ах1, х2) = (х1, Ах2) = (х1, λ2х2) = λ2(х1, х2) (2)
Приравнивая правые части соотношений, получаем
Λ1(х1, х2) = λ2(х1, х2)
Или (λ1 – λ2)(х1, х2) = 0 (3)
Так как λ1= λ2, из равенства (3) следует, что (х1, х2) = 0, что и означает ортогональность векторов х1 и х2
Ответ на вопрос 90
Векторным ( Линейным пространством) называется множество V( произвольной природы) из так называемых векторов, в котором введена операция сложения и неалгебраическая операция умножения вектора на скаляр.
Примеры:
1) Множество свободных векторов из аналитической геометрии.
2) Множество матриц одного размера.
3) Множество решений однородной системы линейных уравнений образует линейное пространство.
№91
U наз-сяподпространством пространства V, если оно само является векторным пространством над полем P.
Критерий подпространства. Непустое множество 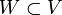 является подпространством пространства V,Т и ТТ, когда W замкнуто относительно сложения векторов и умножения их на скаляры. Иными словами, выполняются следующие условия:1.
является подпространством пространства V,Т и ТТ, когда W замкнуто относительно сложения векторов и умножения их на скаляры. Иными словами, выполняются следующие условия:1. 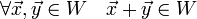 ; 2.
; 2. 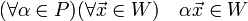 (W=U)
(W=U)
№92 = № 93
Пусть А = {а1, а2 ... ак} (а-вектор) - система векторов из векторного пространства V над полем P.
Определение 2: Линейной оболочкой L системы A называется множество всех линейных комбинаций векторов системы A. Обозначение L(а1, а2, ..., ак).
№94
Система векторов а1, а2... ак 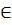 V наз-ся линейно зависимой (ЛЗ), если можно составить нулевую комбинацию этих векторов, в которой не все Лi = 0 т. е. существует нулевая нетривиальная ЛК.
V наз-ся линейно зависимой (ЛЗ), если можно составить нулевую комбинацию этих векторов, в которой не все Лi = 0 т. е. существует нулевая нетривиальная ЛК.
(если один из ее векторов можно представить в виде ЛК остальных векторов системы.) – это еще один вариант определения.
Покажем, что A={ 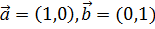 } – линейно-зависимая система.
} – линейно-зависимая система.
Решение. 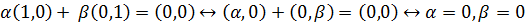 сл-но А – линейно-зависимая система.
сл-но А – линейно-зависимая система.
№95
Система векторов а1, а2... ак с V наз-ся линейно независимой (ЛНЗ), если нельзя составить нулевую комбинацию этих векторов, в которой не все Лi = 0 т. е. нулевая ЛК может быть только тривиальной.
(если ни один из ее векторов нельзя представить в виде ЛК остальных векторов системы.)
Покажем, что A={ 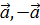 } - линейно-независимая система.
} - линейно-независимая система.
Решение. Найдём нетривиальную комбинацию, равную 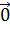 . 1*
. 1*  + 1*(
+ 1*( 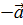 )=
)= 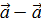 =
= 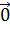 , т.е.
, т.е. 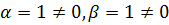
96)Базисом в линейном пространстве называется набор линейно независимых векторов, такой, что любой вектор этого пространства может быть представлен в виде линейной комбинации базисных векторов.
Пример:

97)Базисом в линейном пространстве называется набор линейно независимых векторов, такой, что любой вектор этого пространства может быть представлен в виде линейной комбинации базисных векторов.
Пример:

98)Рангом системы векторов называется число векторов в любом ее базисе. Ранг системы векторов А1,А2,…,Аmбудем обозначать символом r(А1,А2,…,Аm).
Пример:


99)

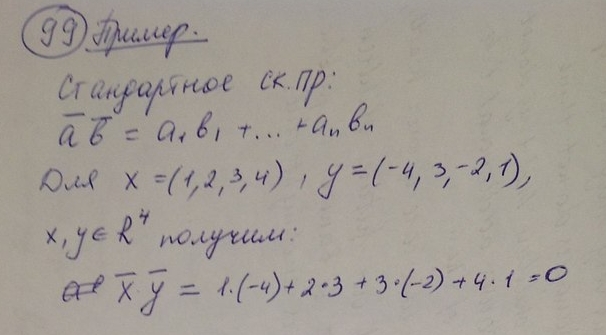
100)
Теория из 99 вопроса.
Пример:

№101.
Евклидовым Е (унитарным U) пространством называется векторное пространство над полем действительных (комплексных) чисел, в котором каждой паре векторов x, y поставлено в соответствие действительное (комплексное) число, которое обозначается через xy и называется скалярным произведением векторов x и y, причем выполняются следующие условия:
1. xy = yx;
2. ( x + y)z = xz + yz;
3. ( αx)y = α(xy);
4. xx > 0, если x≠0;
Длиной вектора а ( т.е.  ) в евклидовом ВП (
) в евклидовом ВП ( 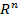 ) называется величина:
) называется величина: 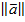 =
= 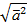 . При n=2 или n=3 длина вектора – тоже самое, что и модуль геометрического вектора, т.е:
. При n=2 или n=3 длина вектора – тоже самое, что и модуль геометрического вектора, т.е:
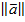 = =
= = 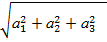
Пример: Пусть  ϵ E2 и его координаты (2; -7). Длина
ϵ E2 и его координаты (2; -7). Длина  :
: 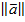 =
= 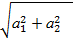 =
= 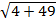 =
= 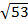 . Ответ:
. Ответ: 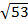
№102.
Евклидовым Е(унитарным U) пространством называется векторное пространство над полем действительных (комплексных) чисел, в котором каждой паре векторов x, y поставлено в соответствие действительное (комплексное) число, которое обозначается через xy и называется скалярным произведением векторов x и y, причем выполняются следующие условия:
1. xy = yx;
2. ( x + y)z = xz + yz;
3. ( αx)y = α(xy);
4. xx > 0, если x≠0;
Углом ϕмежду парой векторов x и y мы будем называть тот угол (в пределах от 0o до 180o ), косинус которого равен отношению: 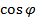 =
= 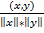 , где
, где 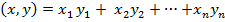 - скалярное произведение векторов. Для того, чтобы можно было пользоваться формулой в произвольном евклидовом пространстве Е, нам надо показать, что
- скалярное произведение векторов. Для того, чтобы можно было пользоваться формулой в произвольном евклидовом пространстве Е, нам надо показать, что 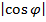 ≤1, для любых векторов x, yϵ Е.
≤1, для любых векторов x, yϵ Е.
Пример: Пусть  и
и 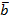 ϵ R2 с координатами,
ϵ R2 с координатами,  = (5;3) и
= (5;3) и 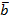 = (7;1).
= (7;1).
Решение:
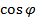 =
= 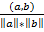 .
.
1. Найду 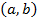 =
= 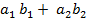 = 5*7+ 3*1 = 35 + 3 = 38
= 5*7+ 3*1 = 35 + 3 = 38
2. Найду 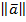 =
= 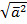 =
= 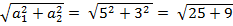 =
= 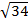 и
и 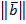 =
= 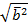 =
= 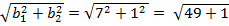 =
= 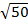
3. Получается, что 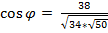 =
= 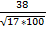 =
= 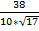 =
= 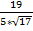 =
= 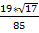
Ответ: 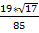
№103.
Система 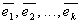 векторов евклидова пространства называетсяортогональной, если векторы системы попарно ортогональны. ( Векторы
векторов евклидова пространства называетсяортогональной, если векторы системы попарно ортогональны. ( Векторы 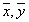 из произвольного евклидова пространства называютсяортогональными, если
из произвольного евклидова пространства называютсяортогональными, если 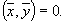 )
)
Примерортогональной системы векторов R3, не являющейся базисом в этом линейном пространстве: 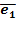 =(1;4;-5)
=(1;4;-5)
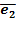 =(-1;4;3)
=(-1;4;3)
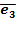 =(0;0;0)
=(0;0;0)
№104.
Ортогональная система 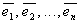 векторов n-мерного евклидова пространства называетсяортонормированной, если все векторы системы имеют единичную длину, т.е. равны 1.
векторов n-мерного евклидова пространства называетсяортонормированной, если все векторы системы имеют единичную длину, т.е. равны 1.
Примерортогональной, но не ортонормированной, системы векторов в R3:
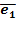 =(0;1;-3)
=(0;1;-3)
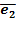 =(2;18;6)
=(2;18;6)
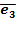 =(-60;6;2)
=(-60;6;2)
№105.
Количество n элементов e1,...,en n-мерного евклидова пространства Е образуют ортонормированный базис этого пространства, если эти элементы попарно ортогональны и норма каждого из этих элементов равна единице, т. е. если
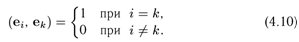
Ортогональный базис — базис, составленный из попарно ортогональныхвекторов. . ( Векторы 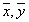 из произвольного евклидова пространства называются ортогональными, если
из произвольного евклидова пространства называются ортогональными, если 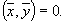 )
)
Примерортонормированного базиса в R3: 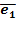 = (1, 0, 0)
= (1, 0, 0)
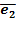 = (0, 1, 0)
= (0, 1, 0)
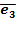 = (0, 0, 1)
= (0, 0, 1)
№111
1) Суммой матриц А и В называют матрицу (А+В)и определяют следующим образом:
А+В=(aij+bij)mxn – поэлементное сложение
Основные свойства:
1. А+(В+С)=(А+В)+С – ассоциативность
2. А+В=В+А – коммутативность
3. А+Оmхn=А – есть в матрице нейтральный элемент по сложению
4. Существует противоположная матрица – А+(-А)=Оmxn, т.е. существует
(-А)= 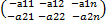
5. (A + B)^T = B^T + A^T
2) Произведением скаляра 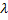 на матрицу А, называется матрица, обозначаемая или определяемая (λ*aij)= λ*A.
на матрицу А, называется матрица, обозначаемая или определяемая (λ*aij)= λ*A.
Основные свойства:
1. (α*β)*А = α*(А*β) – ассоциативность по скалярам
2. (α+β)*А =α*А + α*β
3. α*(А+β) = αА + αβ
4. 1*А=А -(λ=1 – нейтральный элемент умножения на матрицу)
3) Произведение матриц определяется по формуле:
С=А*В 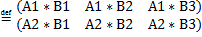
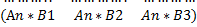 , где
, где
Cij 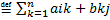 , гдеI и j берутся из i
, гдеI и j берутся из i 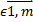 , j ϵ
, j ϵ 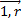
Основные свойства:
1. (AB)C=A(BC) - ассоциативность
2. λ (AB) = (λA) B = A (λB)
3. А(В+С)=АВ+АС
4. (λА)В=А(λВ)
5. ЕА=А; АЕ=А (Е – единичная матрица)
6. В общем случае умножение матриц не коммутативно, т.е. AB не равно ВА
7. 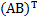 =
= 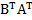
Проверка свойства (AB)C=A(BC):
А= 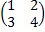 , В=
, В= 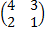 , С=
, С= 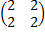
ВС= 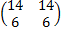 , А(ВС)=
, А(ВС)= 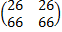
АВ=  , (АВ)С=
, (АВ)С= 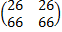 чтд
чтд
№112
1) Суммой матриц А и В называют матрицу (А+В)и определяют следующим образом:
А+В=(aij+bij)mxn – поэлементное сложение
Основные свойства:
1. А+(В+С)=(А+В)+С – ассоциативность
2. А+В=В+А – коммутативность
3. А+Оmхn=А – есть в матрице нейтральный элемент по сложению
4. Существует противоположная матрица – А+(-А)=Оmxn, т.е. существует
(-А)= 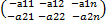
5. (A + B)^T = B^T + A^T
2) Произведением скаляра 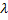 на матрицу А, называется матрица, обозначаемая или определяемая (λ*aij)= λ*A.
на матрицу А, называется матрица, обозначаемая или определяемая (λ*aij)= λ*A.
Основные свойства:
1. (α*β)*А = α*(А*β) – ассоциативность по скалярам
2. (α+β)*А =α*А + α*β
3. α*(А+β) = αА + αβ
4. 1*А=А -(λ=1 – нейтральный элемент умножения на матрицу)
3) Произведение матриц определяется по формуле:
С=А*В 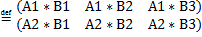
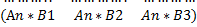 , где
, где
Cij 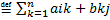 , гдеI и j берутся из i
, гдеI и j берутся из i 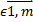 , j ϵ
, j ϵ 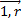
Основные свойства:
1. (AB)C=A(BC) - ассоциативность
2. λ (AB) = (λA) B = A (λB)
3. А(В+С)=АВ+АС
4. (λА)В=А(λВ)
5. ЕА=А; АЕ=А (Е – единичная матрица)
6. В общем случае умножение матриц не коммутативно, т.е. AB не равно ВА
7. 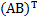 =
= 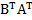
8. Проверка свойства 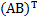 =
= 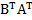 :
:
А= 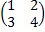 , В=
, В=  ,
, 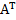 =
= 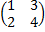 ,
, 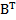 =
=  ,
,
АВ= 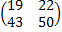 ,
, 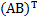 =
= 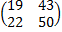 ,
, 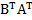 =
= 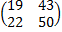 чтд
чтд
№113
Верны свойства: 1,4,5,7,8
№114
Система линейных уравнений называется несовместной, если она не имеет решений.
Совместную систему называют определенной, если есть единственное решение, и неопределенной в противном случае (если есть множество решений).
Несовместная система:
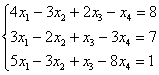 Если количество уравнений меньше, чем количество переменных, то сразу можно сказать, что система либо несовместна, либо имеет бесконечно много решений.
Если количество уравнений меньше, чем количество переменных, то сразу можно сказать, что система либо несовместна, либо имеет бесконечно много решений.
Определенная система:
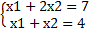 , единственное решение – Х=
, единственное решение – Х= 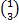
Неопределенная система:
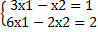
Она имеет множество бесконечных решений вида: 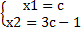 ,где с произвольное число.
,где с произвольное число.
№115
Ранг матрицы – это порядок ее наибольшего ненулевого минора.
Обозначения: r(A), R(A), Rang A.
Примеры: А= 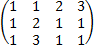 , М3=
, М3=  =1 =>R(A)=3
=1 =>R(A)=3
В= 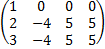 , M2=
, M2= 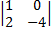 =-4, =>R(B)=2
=-4, =>R(B)=2
C= 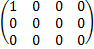 , M1=1,=>R(C)=1
, M1=1,=>R(C)=1
D= 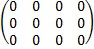 , R(D)=0
, R(D)=0
Ранг матрицы не может равняться 4, т.к. количество строк в матрице равно 3.
116. Сформулируйте теорему Кронекера-Капелли. Приведите примеры совместной и не
совместной систем уравнений, и проиллюстрируйте на них утверждение теоремы
Кронекера-Капелли.
Теорема.
Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы.
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.
117. Что такое фундаментальный набор решений однородной системы линейных
уравнений? Покажите на примере какой-либо однородной системы из двух уравнений с
пятью неизвестными, как её общее решение может быть записано в виде линейной
комбинации решений фундаментального набора.
ФНР ОСЛУ – любой базис в пространстве решений ОСЛУ.
Из определения базиса следует, что любое решение ОСЛУ есть ЛК решений из ФНР (по векторам базиса)
118. Сформулируйте теорему о связи общих решений неоднородной и однородной
систем линейных алгебраических уравнений. Проиллюстрируйте утверждение теоремы на
примере какой-либо неоднородной системы из двух уравнений с пятью неизвестными.
119. Сформулируйте основные свойства определителя матрицы. Проверьте на примере
произвольной ненулевой матрицы 2 × 2 выполнение свойства, связанного с перестановкой
строк.
Свойства определителя.
Пусть Anxnквадратная матрица
1. Определитель не меняется при транспонировании (│А│= │Ат│)
2. При перестановке двух столбцов (или строк) определитель меняет знак.
3. Общий множитель одной стоки можно вынести за знак определителя.
4. Определитель равен 0, если имеет:
a. Нулевую строку(столбец)
b. 2 одинаковые строки(столбца)
c. 2 строки(столбца), элементы которой пропорциональны.
5. Определитель не изменится, если к любой его строке добавить другую строку, умноженную на произвольное число (то же для столбцов)
6. Определитель диагональной матрицы равен произведению элементов главной диагонали
7. Определитель треугольной матрицы равен произведению элементов главной диагонали
8. Определитель произведения двух квадратных матриц равен произведению определителей, т.е. если C=Amxn*Bnxn, то │С│=│А│*│В│
120. Сформулируйте основные свойства определителя матрицы. Проверьте на примере
произвольной ненулевой матрицы 2 × 2 выполнение свойства, связанного с
транспонированием строк.
Свойства определителя.
Пусть Anxnквадратная матрица
1. Определитель не меняется при транспонировании (│А│= │Ат│)
2. При перестановке двух столбцов (или строк) определитель меняет знак.
3. Общий множитель одной стоки можно вынести за знак определителя.
4. Определитель равен 0, если имеет:
a. Нулевую строку(столбец)
b. 2 одинаковые строки(столбца)
c. 2 строки(столбца), элементы которой пропорциональны.
5. Определитель не изменится, если к любой его строке добавить другую строку, умноженную на произвольное число (то же для столбцов)
6. Определитель диагональной матрицы равен произведению элементов главной диагонали
7. Определитель треугольной матрицы равен произведению элементов главной диагонали
8. Определитель произведения двух квадратных матриц равен произведению определителей, т.е. если C=Amxn*Bnxn, то │С│=│А│*│В│
131. Дайте определение обратной матрицы. Как связаны определители матрицы и ее обратной? Приведите пример квадратной матрицы, не имеющей обратной.
Обратная матрица квадратной матрицы А – это матрица А-1, такая, что их произведение = Е( единичной матрице). 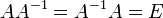
Определители матрицы и ее обратной связаны таким образом, что для нахождения обратной матрицы, нужно найти определитель матрицы.
По опр.23 Квадратная матрица А называется вырожденной (особенной), если ее определитель = 0 (т.е. матрица, не имеющая обратной), и невырожденной в противном случае.
Пример квадратной матрицы, не имеющей обратной:
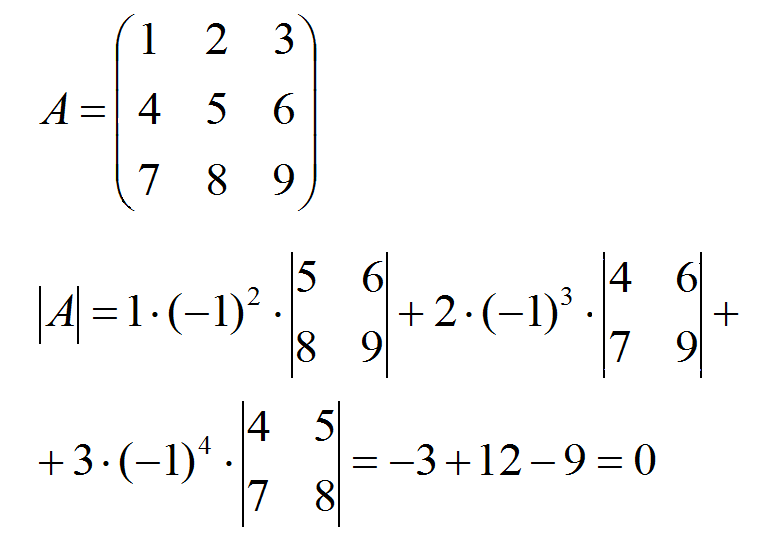
132. Дайте определение модуля и аргумента КЧ. Сформулируйте правило умножения КЧ в тригонометрическом виде и вычислите квадрат мнимой единицы.
Модулем (абсолютной величиной) комплексного числа называется длина радиус-вектора соответствующей точки комплексной плоскости или, что то же, расстояние между точкой комплексной плоскости, соответствующей этому числу, и началом координат).
Модуль комплексного числа 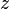 обозначается
обозначается 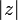 и определяется выражением
и определяется выражением 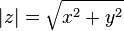 .
.
Угол 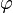 (в радианах) радиус-вектора точки, соответствующей числу
(в радианах) радиус-вектора точки, соответствующей числу 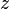 , называется аргументом числа
, называется аргументом числа 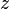 и обозначается
и обозначается 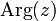 .
.
Тригонометрич. форма КЧ: Z=r(cos