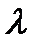Определение базиса Линейного пространства.
Пусть 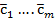 сист.в-ров.
сист.в-ров.
Подсистема 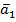 ,….
,…. 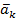
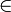
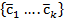 наз-ся макс. ЛНЗ подсист, если добавлением к ней любого в-ра (
наз-ся макс. ЛНЗ подсист, если добавлением к ней любого в-ра ( 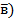 дает уже ЛЗ подсист. Любая макс. ЛНЗ подсист. наз-ся базисом для
дает уже ЛЗ подсист. Любая макс. ЛНЗ подсист. наз-ся базисом для 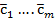 .
.
Другими словами базис-это часть в-ров сист, к-ая ЛНЗ и через к-ую линейно выражается любой в-р системы. Если сист. в-ров имеет несколько базисов, то все они имеют равное число в-ров.

Вопрос 11. Система уравнений называется несовместной, если она не имеет ни одного решения.
Вопрос 12. Любой базис в пространстве решений однородной системы уравнений называется фундаментальным набором решений (ФНР ОСЛУ).
Вопрос 13. Рангом матрицы Аmxn называется максимальный порядок её минора отличный от нуля. Обозначают r(A). Очевидно, что r(A)≤min(m,n)
Вопрос 14. Квадратная матрица называется вырожденной (особенной), если её определитель равен нулю (|А|=0) и невырожденной в противном случае.
Вопрос 15. Квадратная матрица называется ортогональной, если выполняется условие АТА=Е, или согласно определению обратной матрицы: А-1=АТ
№16 (Правило умножения матриц и его свойства)
Произведением Аm*n * Bn*r называется матрица АВ=Сm*r, чей общий член Сij – есть произведение строки Аi на столбец Вj
Свойства умножения матриц: (для матриц Аm*n , Вn*p , Cp*r)
1) (AB)C=A(BC) – ассоциативность
2) (А+В)С=АС+ВС – аддитивность
3) А(В+С)=АВ+АС – дистрибутивность
4) ЕА=А; АЕ=А
5) Умножение матриц не коммутативно
№17 (Обратная матрица и ее свойства)
Квадратная матрица, обозначаемая А-1, называется обратной к квадратной матрице А, если эти матрицы перестановочны и выполняется: А-1 * А=А*А-1=Е
Свойства обратной матрицы:
1) (А-1)-1=А
2) Если А-1 существует, то она – единственная
3) (Ат)-1=(А-1)т
4) (АВ)-1=В-1А-1 (Если квадратные матрицы А и В имеют один размер и обратимы, то их произведение тоже обратимо)
№18 (Свойства определителя матрицы)
1) |A|=|AT|
2) При перестановке двух столбцов/строк определитель меняет знак
3) Общий множитель одной строки/столбца можно вынести за знак определителя
4) Определитель равен 0, если он имеет:
А) нулевую строку/столбец
Б) две одинаковые строки/столбца
В) две строки/столбца, элементы которых пропорциональны
5) Определитель не изменится, если к любой его строке добавить другую строку, умноженную на произвольное число, то же для столбцов.
6) Определитель диагональной матрицы равен произведению элементов главной диагонали
7) Определитель треугольной матрицы равен произведению элементов главной диагонали
8) Определитель произведения двух квадратных матриц равен произведению их определителей
№19 (Теоремы о целых и рациональных корнях многочленов с целыми коэффициентами)
Теорема о рациональных корнях многочленов с целыми коэффициентами: Пусть рациональное число p/q – корень многочлена с целыми коэффициентами, причем дробь p/q – несократимая. Тогда числитель дроби p – делитель свободного члена, а знаменатель q – делитель старшего коэффициента многочлена.
Теорема о целых корнях многочленов с целыми коэффициентами: Всякий целый корень многочлена с целыми коэффициентами является делителем его свободного члена.
№20 (Теорема Безу и следствия из нее)
Теорема Безу: Пусть f – многочлен, c – некоторое число. Тогда:
1) f делится на x – c только, если число c является его корнем;
2) остаток от деления f на x – c равен f(c).
Следствия:
Следствие 1. Два многочлена степени, не большей n, принимают одинаковые значения при n + 1 значении x тогда и только тогда, когда при каждой степени x они имеют одинаковые коэффициенты.
Следствие 2. Два многочлена принимают одинаковые значения при всех значениях x тогда и только тогда, когда при каждой степени x они имеют одинаковые коэффициенты.
21)
Модулем |Z| комплексного числа (КЧ)z=a+biназ-ся действительное число z = 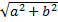 или |Z|=
или |Z|= 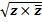 .(длина радиус-вектора соответствующей точки комплексной пл-ти)
.(длина радиус-вектора соответствующей точки комплексной пл-ти)
Угол 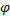 (в радианах) радиус-вектора точки, соответствующей числу z, наз-ся аргументом числа z и обозначается arg(z).
(в радианах) радиус-вектора точки, соответствующей числу z, наз-ся аргументом числа z и обозначается arg(z).
22)
Формула Муавра.Эта ф-ла позволяет возводить в целую степень ненулевое КЧ, представленное в тригонометрической форме. 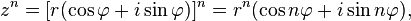 где r — модуль, а
где r — модуль, а 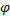 — аргумент комплексного числа. В совр. символике она опубликована Эйлером в 1722 году. Приведенная формуле справедлива при любом целом n, не обязательно положительном.
— аргумент комплексного числа. В совр. символике она опубликована Эйлером в 1722 году. Приведенная формуле справедлива при любом целом n, не обязательно положительном.
23)
Основная теорема алгебры. Всякий мн-н над полем е КЧ имеет корень в этом поле. Сл-е: любой мн-н Pn(x) 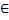 C[x] степени
C[x] степени 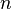 над полем комплексных чисел имеет в нём ровно
над полем комплексных чисел имеет в нём ровно 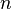 корней, с учётом кратности корней.
корней, с учётом кратности корней.
24)
Пусть V – векторное пространство (ВП). Линейный оператор – это отображение f: V 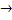 V, если оно удовлетворяет условия линейности, т. е. сущ-ют
V, если оно удовлетворяет условия линейности, т. е. сущ-ют 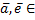 V и скаляр Л
V и скаляр Л 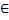 F. f(
F. f( 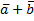 ) = f(
) = f( 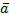 ) + f(
) + f( 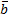 ); f(л
); f(л 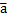 ) = л f(
) = л f( 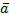 );
);
25)
Ненулевой вектор наз-ся собственным вектором ЛО 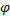 , если существует скаляр Л, такой что
, если существует скаляр Л, такой что 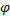 (
( 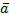 )=Л(
)=Л( 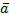 ). Скаляр Л наз-ся собственным значением ЛО.
). Скаляр Л наз-ся собственным значением ЛО.
26)
Вектор столбец 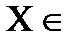
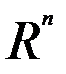 является свободным вектором квадратной матрицы A, если 1)
является свободным вектором квадратной матрицы A, если 1) 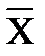
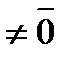 ; 2) существует скаляр
; 2) существует скаляр 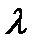 ,который является свободным значением матрицы, такой что АХ=Х
,который является свободным значением матрицы, такой что АХ=Х