Дайте определение линейного пространства.
Дайте определение линейного пространства.
Векторным пространством (ВП) – называется множество V произвольной природы, состоящих из так называемых векторов, которым введена: алгебраическая операция сложения (+) и не алгебраическая операция умножение на скаляр, то есть произвольное число.
Дайте определение подпространства линейного пространства.
Пусть V-линейное пространство, а L-произвольное подмножество (L 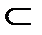 V). Подмножество L называется подпространством линейного пространства V, если оно само является линейным пространством относительно тех же операций сложения и умножения на число, что определены в
V). Подмножество L называется подпространством линейного пространства V, если оно само является линейным пространством относительно тех же операций сложения и умножения на число, что определены в
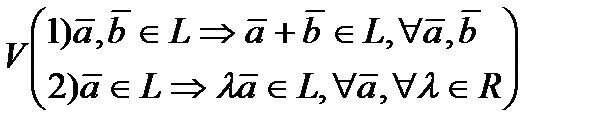
Критерии подпространств:
1) для любых двух векторов 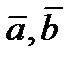 из L их сумма
из L их сумма 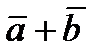 также принадлежит L
также принадлежит L
2) для любого вектора 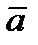 из L и любого действительного числа λ произведение λ
из L и любого действительного числа λ произведение λ 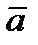 также принадлежит L
также принадлежит L
Примеры:
1) Множество всех многочленов, заданных на отрезке [a;b]-подпространством линейного пространства функций, заданных на этом отрезке.
2) Множество всех многочленов, степень которых не превышает n-1, является подпространством множества многочленов, степень которых не превышает n.
3) Множество решений однородной системы линейных уравнений с n неизвестными является подпространством пространства R 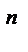 .
.
dimV≥dimL, где V-линейное пространство, L-его подпростр-во.
Свойства подпространств:
· Подпространство линейного пространства есть линейное пространство
· Размерность подпространства не больше размерности линейного пространства.
· Если e1, e2, e3 – базис подпространства линейного пространства, то
· ek+1, ek+2, ¼enÎR так что, e1, e2¼ek¼en – базис в R.
Определение ЛЗ и ЛНЗ системы векторов
Система векторов 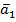 ,….
,…. 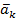 называется Линейно Зависимой, если можно составить нулевую ЛК этих векторов:
называется Линейно Зависимой, если можно составить нулевую ЛК этих векторов: 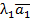 +…+
+…+ 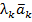 =
= 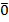 , в к-ой не все коэф-ты (
, в к-ой не все коэф-ты ( 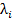 =0), т.е. сущ-ет нулевая нетривиальная ЛК.
=0), т.е. сущ-ет нулевая нетривиальная ЛК.
В противном случае (когда нулевая ЛК может быть только тривиальной) сист. наз-ся ЛНЗ.
Система в-ров 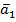 ,….
,…. 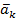
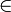 V, наз-ся ЛЗ, если 1 из ее в-ров можно представить в виде ЛК остальных в-ров системы, и ЛНЗ в противном случае.
V, наз-ся ЛЗ, если 1 из ее в-ров можно представить в виде ЛК остальных в-ров системы, и ЛНЗ в противном случае.
22)
Формула Муавра.Эта ф-ла позволяет возводить в целую степень ненулевое КЧ, представленное в тригонометрической форме. 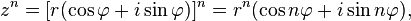 где r — модуль, а
где r — модуль, а 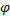 — аргумент комплексного числа. В совр. символике она опубликована Эйлером в 1722 году. Приведенная формуле справедлива при любом целом n, не обязательно положительном.
— аргумент комплексного числа. В совр. символике она опубликована Эйлером в 1722 году. Приведенная формуле справедлива при любом целом n, не обязательно положительном.
23)
Основная теорема алгебры. Всякий мн-н над полем е КЧ имеет корень в этом поле. Сл-е: любой мн-н Pn(x) 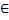 C[x] степени
C[x] степени 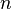 над полем комплексных чисел имеет в нём ровно
над полем комплексных чисел имеет в нём ровно 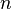 корней, с учётом кратности корней.
корней, с учётом кратности корней.
24)
Пусть V – векторное пространство (ВП). Линейный оператор – это отображение f: V 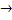 V, если оно удовлетворяет условия линейности, т. е. сущ-ют
V, если оно удовлетворяет условия линейности, т. е. сущ-ют 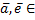 V и скаляр Л
V и скаляр Л 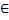 F. f(
F. f( 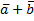 ) = f(
) = f( 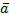 ) + f(
) + f( 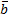 ); f(л
); f(л 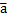 ) = л f(
) = л f( 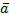 );
);
25)
Ненулевой вектор наз-ся собственным вектором ЛО 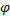 , если существует скаляр Л, такой что
, если существует скаляр Л, такой что 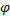 (
( 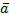 )=Л(
)=Л( 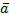 ). Скаляр Л наз-ся собственным значением ЛО.
). Скаляр Л наз-ся собственным значением ЛО.
26)
Вектор столбец 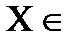
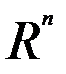 является свободным вектором квадратной матрицы A, если 1)
является свободным вектором квадратной матрицы A, если 1) 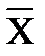
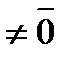 ; 2) существует скаляр
; 2) существует скаляр 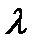 ,который является свободным значением матрицы, такой что АХ=Х
,который является свободным значением матрицы, такой что АХ=Х 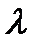
Закон инерции
Число слагаемых с положительными (отрицательными) коэффициентами в квадратичной форме канонического вида не зависит от линейного преобразования, приводящего к этому каноническому виду.
Критерий Сильвестра
а) Квадратичная форма положительно определена тогда и только тогда, когда все так называемые угловые миноры матрицы А положительны.
б) Квадратичная форма отрицательно определена тогда и только тогда, когда знаки её угловых миноров чередуются ( 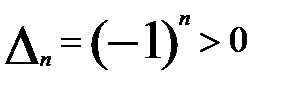
При нарушении а или б квадратичная форма будет знако-неопределенной.
30) Формула расстояния между точками в многомерном пространстве 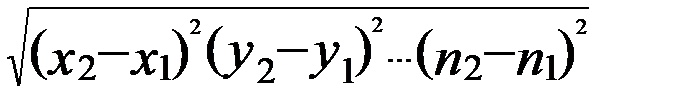
Выпуклых множеств.
Пусть 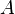 — векторное пространство (над полем вещественных чисел
— векторное пространство (над полем вещественных чисел 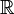 ).
).
Множество 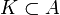 называется выпуклым, если вместе с любыми двумя точками
называется выпуклым, если вместе с любыми двумя точками 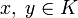 множеству
множеству 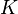 принадлежат все точки отрезка
принадлежат все точки отрезка 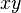 , соединяющего в пространстве
, соединяющего в пространстве 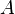 точки
точки 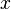 и
и 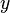 . Этот отрезок можно представить как
. Этот отрезок можно представить как
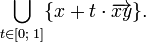
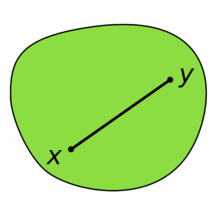 выпуклое
выпуклое 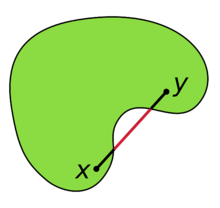 невыпуклое
невыпуклое
Свойства
Выпуклое множество в топологическом линейном пространстве является связным и линейно связным, гомотопически эквивалентным точке. В терминах связности, выпуклое множество можно определить так: множество выпукло, если его пересечение с любой (вещественной) прямой связно. Пусть 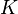 — выпуклое множество. Тогда для любых элементов
— выпуклое множество. Тогда для любых элементов 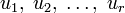 принадлежащих
принадлежащих 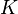 и для всех неотрицательных
и для всех неотрицательных 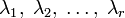 , таких что
, таких что 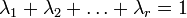 , вектор
, вектор 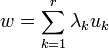 принадлежит
принадлежит 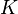 .
.
Вектор 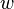 называется выпуклой комбинацией элементов
называется выпуклой комбинацией элементов 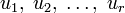 .
.
· Пересечение любого числа выпуклых множеств является выпуклым множеством, таким образом выпуклые подмножества образуют полную сетку. Это так же означает и то, что любое подмножество 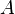 линейного пространства содержится внутри малого выпуклого множества (называемого выпуклой оболочкой множества
линейного пространства содержится внутри малого выпуклого множества (называемого выпуклой оболочкой множества 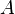 ), то есть пересечение всех выпуклых множеств содержит
), то есть пересечение всех выпуклых множеств содержит 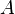 .
.
· Замкнутые выпуклые множества могут быть определены как пересечения замкнутых полупространств (множества точек в пространстве, которые лежат только на одной частигиперплоскости). Из выше сказанного становится понятным, что такие пересечения являются выпуклыми и замкнутыми множествами. Для доказательства обратного, то есть что каждое выпуклое множество может быть представлено в виде пересечения, можно использовать теорему об опорной гиперплоскости в форме в которой для данного замкнутого выпуклого множества 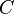 и точки
и точки 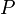 , не принадлежащей ему, существует замкнутое полупространство
, не принадлежащей ему, существует замкнутое полупространство 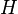 , содержащее
, содержащее 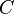 и не содержащее
и не содержащее 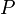 . Теорема об опорной гиперплоскости является частным случаем теоремы Хана — Банаха из функционального анализа.
. Теорема об опорной гиперплоскости является частным случаем теоремы Хана — Банаха из функционального анализа.
· Теорема Хелли: Предположим в конечном семействе выпуклых подмножеств 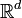 , пересечение любых
, пересечение любых 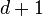 из них непусто. Тогда пересечение всех подмножеств из этого семейства непусто.
из них непусто. Тогда пересечение всех подмножеств из этого семейства непусто.
· Любое выпуклое множество единичной площади в 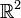 можно целиком заключить в некоторый треугольник площади 2.[1]
можно целиком заключить в некоторый треугольник площади 2.[1]
Каноническое уравнение
Для любого эллипса можно найти декартову систему координат такую, что эллипс будет описываться уравнением (каноническое уравнение эллипса):
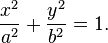
Оно описывает эллипс с центром в начале координат, оси которого совпадают с осями координат.
99)

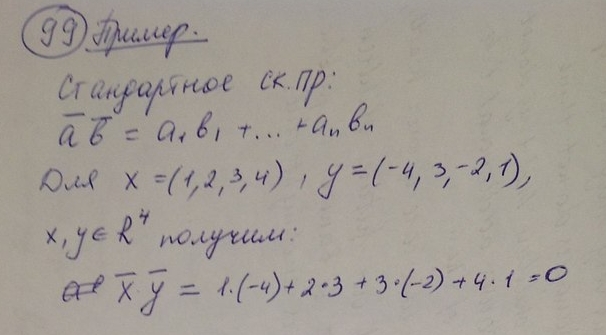
100)
Теория из 99 вопроса.
Пример:

№101.
Евклидовым Е (унитарным U) пространством называется векторное пространство над полем действительных (комплексных) чисел, в котором каждой паре векторов x, y поставлено в соответствие действительное (комплексное) число, которое обозначается через xy и называется скалярным произведением векторов x и y, причем выполняются следующие условия:
1. xy = yx;
2. ( x + y)z = xz + yz;
3. ( αx)y = α(xy);
4. xx > 0, если x≠0;
Длиной вектора а ( т.е.  ) в евклидовом ВП (
) в евклидовом ВП ( 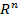 ) называется величина:
) называется величина: 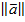 =
= 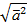 . При n=2 или n=3 длина вектора – тоже самое, что и модуль геометрического вектора, т.е:
. При n=2 или n=3 длина вектора – тоже самое, что и модуль геометрического вектора, т.е:
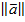 = =
= = 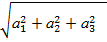
Пример: Пусть  ϵ E2 и его координаты (2; -7). Длина
ϵ E2 и его координаты (2; -7). Длина  :
: 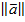 =
= 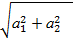 =
= 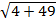 =
= 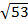 . Ответ:
. Ответ: 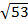
№102.
Евклидовым Е(унитарным U) пространством называется векторное пространство над полем действительных (комплексных) чисел, в котором каждой паре векторов x, y поставлено в соответствие действительное (комплексное) число, которое обозначается через xy и называется скалярным произведением векторов x и y, причем выполняются следующие условия:
1. xy = yx;
2. ( x + y)z = xz + yz;
3. ( αx)y = α(xy);
4. xx > 0, если x≠0;
Углом ϕмежду парой векторов x и y мы будем называть тот угол (в пределах от 0o до 180o ), косинус которого равен отношению: 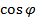 =
= 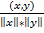 , где
, где 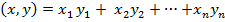 - скалярное произведение векторов. Для того, чтобы можно было пользоваться формулой в произвольном евклидовом пространстве Е, нам надо показать, что
- скалярное произведение векторов. Для того, чтобы можно было пользоваться формулой в произвольном евклидовом пространстве Е, нам надо показать, что 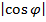 ≤1, для любых векторов x, yϵ Е.
≤1, для любых векторов x, yϵ Е.
Пример: Пусть  и
и 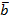 ϵ R2 с координатами,
ϵ R2 с координатами,  = (5;3) и
= (5;3) и 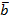 = (7;1).
= (7;1).
Решение:
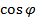 =
= 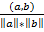 .
.
1. Найду 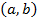 =
= 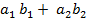 = 5*7+ 3*1 = 35 + 3 = 38
= 5*7+ 3*1 = 35 + 3 = 38
2. Найду 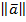 =
= 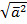 =
= 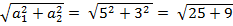 =
= 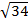 и
и 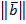 =
= 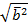 =
= 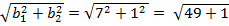 =
= 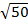
3. Получается, что 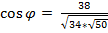 =
= 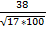 =
= 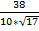 =
= 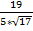 =
= 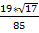
Ответ: 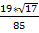
№103.
Система 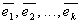 векторов евклидова пространства называетсяортогональной, если векторы системы попарно ортогональны. ( Векторы
векторов евклидова пространства называетсяортогональной, если векторы системы попарно ортогональны. ( Векторы 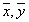 из произвольного евклидова пространства называютсяортогональными, если
из произвольного евклидова пространства называютсяортогональными, если 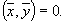 )
)
Примерортогональной системы векторов R3, не являющейся базисом в этом линейном пространстве: 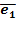 =(1;4;-5)
=(1;4;-5)
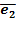 =(-1;4;3)
=(-1;4;3)
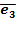 =(0;0;0)
=(0;0;0)
№104.
Ортогональная система 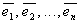 векторов n-мерного евклидова пространства называетсяортонормированной, если все векторы системы имеют единичную длину, т.е. равны 1.
векторов n-мерного евклидова пространства называетсяортонормированной, если все векторы системы имеют единичную длину, т.е. равны 1.
Примерортогональной, но не ортонормированной, системы векторов в R3:
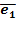 =(0;1;-3)
=(0;1;-3)
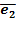 =(2;18;6)
=(2;18;6)
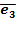 =(-60;6;2)
=(-60;6;2)
№105.
Количество n элементов e1,...,en n-мерного евклидова пространства Е образуют ортонормированный базис этого пространства, если эти элементы попарно ортогональны и норма каждого из этих элементов равна единице, т. е. если
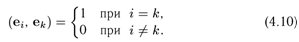
Ортогональный базис — базис, составленный из попарно ортогональныхвекторов. . ( Векторы 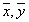 из произвольного евклидова пространства называются ортогональными, если
из произвольного евклидова пространства называются ортогональными, если 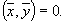 )
)
Примерортонормированного базиса в R3: 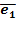 = (1, 0, 0)
= (1, 0, 0)
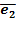 = (0, 1, 0)
= (0, 1, 0)
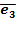 = (0, 0, 1)
= (0, 0, 1)
№111
1) Суммой матриц А и В называют матрицу (А+В)и определяют следующим образом:
А+В=(aij+bij)mxn – поэлементное сложение
Основные свойства:
1. А+(В+С)=(А+В)+С – ассоциативность
2. А+В=В+А – коммутативность
3. А+Оmхn=А – есть в матрице нейтральный элемент по сложению
4. Существует противоположная матрица – А+(-А)=Оmxn, т.е. существует
(-А)= 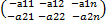
5. (A + B)^T = B^T + A^T
2) Произведением скаляра 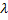 на матрицу А, называется матрица, обозначаемая или определяемая (λ*aij)= λ*A.
на матрицу А, называется матрица, обозначаемая или определяемая (λ*aij)= λ*A.
Основные свойства:
1. (α*β)*А = α*(А*β) – ассоциативность по скалярам
2. (α+β)*А =α*А + α*β
3. α*(А+β) = αА + αβ
4. 1*А=А -(λ=1 – нейтральный элемент умножения на матрицу)
3) Произведение матриц определяется по формуле:
С=А*В 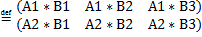
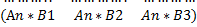 , где
, где
Cij 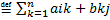 , гдеI и j берутся из i
, гдеI и j берутся из i 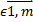 , j ϵ
, j ϵ 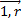
Основные свойства:
1. (AB)C=A(BC) - ассоциативность
2. λ (AB) = (λA) B = A (λB)
3. А(В+С)=АВ+АС
4. (λА)В=А(λВ)
5. ЕА=А; АЕ=А (Е – единичная матрица)
6. В общем случае умножение матриц не коммутативно, т.е. AB не равно ВА
7. 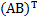 =
= 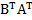
Проверка свойства (AB)C=A(BC):
А= 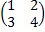 , В=
, В= 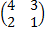 , С=
, С= 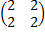
ВС= 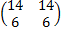 , А(ВС)=
, А(ВС)= 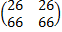
АВ=  , (АВ)С=
, (АВ)С= 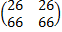 чтд
чтд
№112
1) Суммой матриц А и В называют матрицу (А+В)и определяют следующим образом:
А+В=(aij+bij)mxn – поэлементное сложение
Основные свойства:
1. А+(В+С)=(А+В)+С – ассоциативность
2. А+В=В+А – коммутативность
3. А+Оmхn=А – есть в матрице нейтральный элемент по сложению
4. Существует противоположная матрица – А+(-А)=Оmxn, т.е. существует
(-А)= 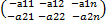
5. (A + B)^T = B^T + A^T
2) Произведением скаляра 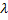 на матрицу А, называется матрица, обозначаемая или определяемая (λ*aij)= λ*A.
на матрицу А, называется матрица, обозначаемая или определяемая (λ*aij)= λ*A.
Основные свойства:
1. (α*β)*А = α*(А*β) – ассоциативность по скалярам
2. (α+β)*А =α*А + α*β
3. α*(А+β) = αА + αβ
4. 1*А=А -(λ=1 – нейтральный элемент умножения на матрицу)
3) Произведение матриц определяется по формуле:
С=А*В 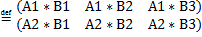
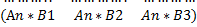 , где
, где
Cij 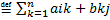 , гдеI и j берутся из i
, гдеI и j берутся из i 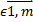 , j ϵ
, j ϵ 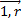
Основные свойства:
1. (AB)C=A(BC) - ассоциативность
2. λ (AB) = (λA) B = A (λB)
3. А(В+С)=АВ+АС
4. (λА)В=А(λВ)
5. ЕА=А; АЕ=А (Е – единичная матрица)
6. В общем случае умножение матриц не коммутативно, т.е. AB не равно ВА
7. 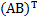 =
= 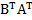
8. Проверка свойства 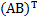 =
= 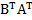 :
:
А= 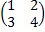 , В=
, В=  ,
, 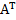 =
= 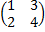 ,
, 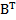 =
=  ,
,
АВ= 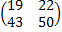 ,
, 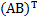 =
= 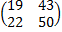 ,
, 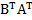 =
= 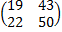 чтд
чтд
№113
Верны свойства: 1,4,5,7,8
№114
Система линейных уравнений называется несовместной, если она не имеет решений.
Совместную систему называют определенной, если есть единственное решение, и неопределенной в противном случае (если есть множество решений).
Несовместная система:
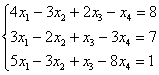 Если количество уравнений меньше, чем количество переменных, то сразу можно сказать, что система либо несовместна, либо имеет бесконечно много решений.
Если количество уравнений меньше, чем количество переменных, то сразу можно сказать, что система либо несовместна, либо имеет бесконечно много решений.
Определенная система:
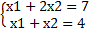 , единственное решение – Х=
, единственное решение – Х= 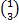
Неопределенная система:
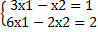
Она имеет множество бесконечных решений вида: 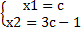 ,где с произвольное число.
,где с произвольное число.
№115
Ранг матрицы – это порядок ее наибольшего ненулевого минора.
Обозначения: r(A), R(A), Rang A.
Примеры: А= 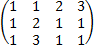 , М3=
, М3=  =1 =>R(A)=3
=1 =>R(A)=3
В= 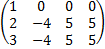 , M2=
, M2= 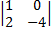 =-4, =>R(B)=2
=-4, =>R(B)=2
C= 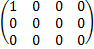 , M1=1,=>R(C)=1
, M1=1,=>R(C)=1
D= 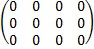 , R(D)=0
, R(D)=0
Ранг матрицы не может равняться 4, т.к. количество строк в матрице равно 3.
116. Сформулируйте теорему Кронекера-Капелли. Приведите примеры совместной и не
совместной систем уравнений, и проиллюстрируйте на них утверждение теоремы
Кронекера-Капелли.
Теорема.
Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы.
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.
117. Что такое фундаментальный набор решений однородной системы линейных
уравнений? Покажите на примере какой-либо однородной системы из двух уравнений с
пятью неизвестными, как её общее решение может быть записано в виде линейной
комбинации решений фундаментального набора.
ФНР ОСЛУ – любой базис в пространстве решений ОСЛУ.
Из определения базиса следует, что любое решение ОСЛУ есть ЛК решений из ФНР (по векторам базиса)
118. Сформулируйте теорему о связи общих решений неоднородной и однородной
систем линейных алгебраических уравнений. Проиллюстрируйте утверждение теоремы на
примере какой-либо неоднородной системы из двух уравнений с пятью неизвестными.
119. Сформулируйте основные свойства определителя матрицы. Проверьте на примере
произвольной ненулевой матрицы 2 × 2 выполнение свойства, связанного с перестановкой
строк.
Свойства определителя.
Пусть Anxnквадратная матрица
1. Определитель не меняется при транспонировании (│А│= │Ат│)
2. При перестановке двух столбцов (или строк) определитель меняет знак.
3. Общий множитель одной стоки можно вынести за знак определителя.
4. Определитель равен 0, если имеет:
a. Нулевую строку(столбец)
b. 2 одинаковые строки(столбца)
c. 2 строки(столбца), элементы которой пропорциональны.
5. Определитель не изменится, если к любой его строке добавить другую строку, умноженную на произвольное число (то же для столбцов)
6. Определитель диагональной матрицы равен произведению элементов главной диагонали
7. Определитель треугольной матрицы равен произведению элементов главной диагонали
8. Определитель произведения двух квадратных матриц равен произведению определителей, т.е. если C=Amxn*Bnxn, то │С│=│А│*│В│
120. Сформулируйте основные свойства определителя матрицы. Проверьте на примере
произвольной ненулевой матрицы 2 × 2 выполнение свойства, связанного с
транспонированием строк.
Свойства определителя.
Пусть Anxnквадратная матрица
1. Определитель не меняется при транспонировании (│А│= │Ат│)
2. При перестановке двух столбцов (или строк) определитель меняет знак.
3. Общий множитель одной стоки можно вынести за знак определителя.
4. Определитель равен 0, если имеет:
a. Нулевую строку(столбец)
b. 2 одинаковые строки(столбца)
c. 2 строки(столбца), элементы которой пропорциональны.
5. Определитель не изменится, если к любой его строке добавить другую строку, умноженную на произвольное число (то же для столбцов)
6. Определитель диагональной матрицы равен произведению элементов главной диагонали
7. Определитель треугольной матрицы равен произведению элементов главной диагонали
8. Определитель произведения двух квадратных матриц равен произведению определителей, т.е. если C=Amxn*Bnxn, то │С│=│А│*│В│
131. Дайте определение обратной матрицы. Как связаны определители матрицы и ее обратной? Приведите пример квадратной матрицы, не имеющей обратной.
Обратная матрица квадратной матрицы А – это матрица А-1, такая, что их произведение = Е( единичной матрице). 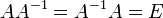
Определители матрицы и ее обратной связаны таким образом, что для нахождения обратной матрицы, нужно найти определитель матрицы.
По опр.23 Квадратная матрица А называется вырожденной (особенной), если ее определитель = 0 (т.е. матрица, не имеющая обратной), и невырожденной в противном случае.
Пример квадратной матрицы, не имеющей обратной:
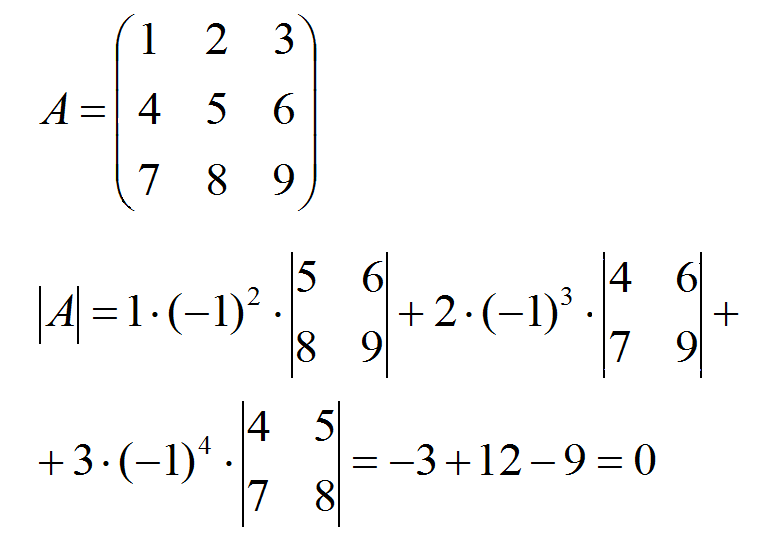
132. Дайте определение модуля и аргумента КЧ. Сформулируйте правило умножения КЧ в тригонометрическом виде и вычислите квадрат мнимой единицы.
Модулем (абсолютной величиной) комплексного числа называется длина радиус-вектора соответствующей точки комплексной плоскости или, что то же, расстояние между точкой комплексной плоскости, соответствующей этому числу, и началом координат).
Модуль комплексного числа 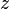 обозначается
обозначается 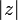 и определяется выражением
и определяется выражением 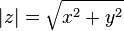 .
.
Угол 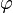 (в радианах) радиус-вектора точки, соответствующей числу
(в радианах) радиус-вектора точки, соответствующей числу 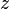 , называется аргументом числа
, называется аргументом числа 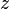 и обозначается
и обозначается 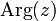 .
.
Тригонометрич. форма КЧ: Z=r(cosφ + sin φ), где r=|z| - модуль КЧ, φ = arg(z) – аргумент КЧ.
Правило умножения комплексных чисел в тригонометрической форме записи:
При умножении КЧ их модули перемножаются, а аргументы складываются
z1z2=r2(cosφ1+ isin φ1)r2*(cos φ2+isin φ2)=r1r2(cos φ1 cos φ2+ i2 sin φ1sin φ2+i(sin φ1cos φ2+cos φ1sin φ2))= r1r2(cos(φ1+ φ2))+ isin(φ1+ φ2).
Квадрат мнимой единицы
I2 = – 1. Число i будем называть мнимой единицей.
Из этого равенства находим 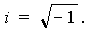
Введение мнимой единицы позволяет извлекать квадратные корни квадратные из отрицательных чисел.
Например,
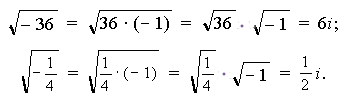
133. Сформулируйте правила деления КЧ в алгебраич. и тригонометрич. виде. Приведите примеры.
Если делимое и делитель даны в алгебраической форме, то правило деления таково: для того, чтобы разделить комплексное число (a1 + b1i ) на другое комплексное число (a2 + b2i ), то есть найти 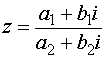 , нужно и числитель, и знаменатель умножить на число, сопряжённое знаменателю.
, нужно и числитель, и знаменатель умножить на число, сопряжённое знаменателю.
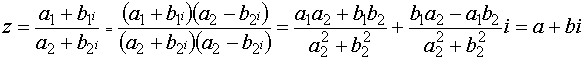
Пусть 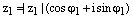 , где
, где 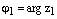 и
и 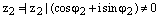 , где
, где 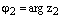 – два произвольных комплексных числа записанных в тригонометрической форме. Тогда
– два произвольных комплексных числа записанных в тригонометрической форме. Тогда
Формула для деления комплексных чисел, заданных в тригонометрической форме:
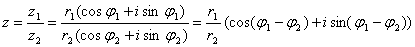
при делении комплексных чисел их модули делятся один на другой, а аргументы вычитаются.
Пример 1. (Алгебраическая форма)
Даны комплексные числа 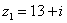 ,
, 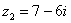 . Найти частное
. Найти частное 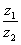 .
.
Составим частное:
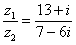
Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.
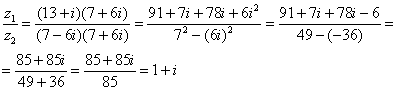
Пример 2. (Тригонометрическая форма)
Запишите комплексные числа 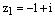 и
и 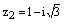 в тригонометрической форме и найдите их частное
в тригонометрической форме и найдите их частное 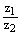 .
.
Решение.
1) Комплексное число 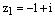 на комплексной плоскости находится во второй четверти, поэтому
на комплексной плоскости находится во второй четверти, поэтому
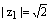 ,
, 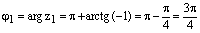 .
.
2) Комплексное число 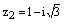 на комплексной плоскости находится во четвертой четверти, поэтому
на комплексной плоскости находится во четвертой четверти, поэтому
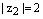 ,
, 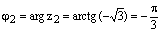 .
.
3) 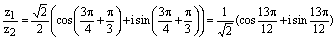
Ответ: 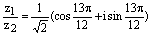 .
.
134. Сформулируйте основную теорему алгебры и следствия из нее, касающиеся разложения на множители произвольных многочленов и многочленов с действительными коэффициентами. Приведите пример многочлена с действительными коэффициентами степени 3, разложение которого на множители представляет собою произведение линейного и квадратичного (с D<0) множителей.
Основная теорема алгебры:
Всякий многочлен над полем С комплексных чисел имеет корень в этом поле.
(Другая формулировка:Всякий многочлен, степень которого не меньше единицы, имеет хотя бы один корень, в общем случае комплексный.)
Следствие 1. Любой многочлен 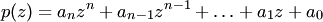 степени
степени 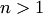 с комплексными коэффициентами
с комплексными коэффициентами 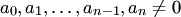 можно представить в виде произведения линейных двучленов:
можно представить в виде произведения линейных двучленов:
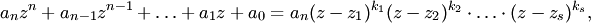
где 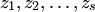 — корни многочлена кратности
— корни многочлена кратности 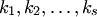 соответственно, причем
соответственно, причем 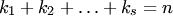 . Другими словами, многочлен n-й степени имеет ровно
. Другими словами, многочлен n-й степени имеет ровно 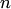 корней, если каждый корень считать столько раз, какова его кратность.
корней, если каждый корень считать столько раз, какова его кратность.
Следствие 2. Если многочлены 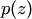 и
и 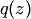 , степени которых не превосходят
, степени которых не превосходят 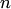 , имеют равные значения более чем при п различных значениях переменной
, имеют равные значения более чем при п различных значениях переменной  , то эти многочлены равны:
, то эти многочлены равны: 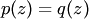 .
.
В самом деле, по условию многочлен 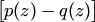 имеет более, чем
имеет более, чем 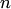 корней, хотя его степень меньше или равна
корней, хотя его степень меньше или равна 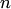 , что противоречит следствию 1 из основной теоремы алгебры. Следовательно, это многочлен нулевой степени
, что противоречит следствию 1 из основной теоремы алгебры. Следовательно, это многочлен нулевой степени 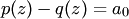 . Так как он имеет корни, то
. Так как он имеет корни, то 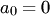 . Следовательно,
. Следовательно, 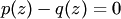 , то есть
, то есть 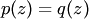 .
.
Следствие 3. Если комплексное (но не действительное) число С — корень многочлена р(с) с действительными коэффициентами, то сопряженное число 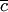 является его корнем той же кратности.
является его корнем той же кратности.
Следствие 4. Всякий многочлен 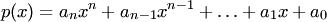 с действительными коэффициентами представляется в виде произведения линейных двучленов и квадратных трехчленов (с отрицательными дискриминантами):
с действительными коэффициентами представляется в виде произведения линейных двучленов и квадратных трехчленов (с отрицательными дискриминантами):
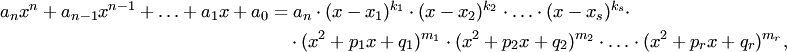
где 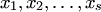 — действительные корни кратности
— действительные корни кратности 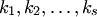 , причем
, причем 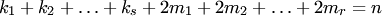 .
.
Следствие 5. Многочлен нечетной степени с действительными коэффициентами всегда имеет хотя бы один действительный корень.
Многочлен четной степени с действительными коэффициентами может не иметь действительных корней.
135. Дайте определение ортогональной матрицы. Приведите пример такой матрицы.
(по опр.11) Квадратная матрица А называется ортогональной, если АтА=Е, или согласно определению обратной матрицы А-1=Ат
Пример ортогональной матрицы: 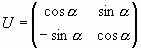
1.Убедимся, что матрица U невырождена:
U= 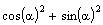 =1 ( ≠ 0 =>невырождена)
=1 ( ≠ 0 =>невырождена)
2. Найдем обратную матрицу 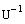 и транспонированную матрицу
и транспонированную матрицу 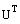
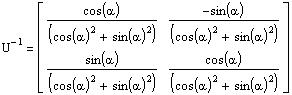
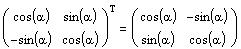
Так как 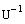 =
=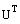 => матрица U ортогональна.
=> матрица U ортогональна.
136.Собственный вектор – ненулевой вектор, такой что, j( 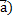 =l
=l 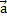 , если существует l.
, если существует l.
Этот скаляр называется собственным значением ЛО.
137.Закон инерции квадратичных форм:
Число слагаемых с положительными и отрицательными коэффициентами в КФ в каноническом виде не зависит от линейного преобразования (ЛПр), приводящего к этому каноническому виду (число положительных коэффициентов = числу отрицательных).
138.Аффинная система координат (косоугольная система координат) — прямолинейная система координат в аффинном пространстве.
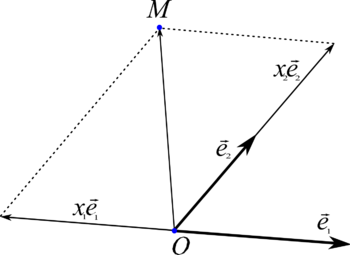
Аффинное пространство — служит обобщением аффинных свойств евклидова пространства. Во многом схоже с векторным пространством, но в отличие от последнего, точки в аффинном пространстве являются равноправными. В частности в аффинном пространстве нет понятия нулевой точки и<
