Метод Эйлера, метод Рунге – Кутты
Основные понятия:численные методы решений дифференциальных уравнений [1, с. 425-428]
Рассмотрим задачу Коши для дифференциального уравнения первого порядка, разрешенного относительно производной
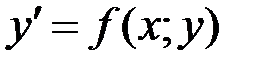 ,
, 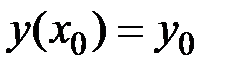 .
.
Требуется найти решение на отрезке 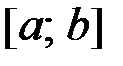 , где
, где 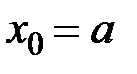 .
.
Разобьем отрезок 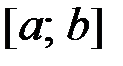 на
на 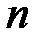 равных частей и получим последовательность
равных частей и получим последовательность 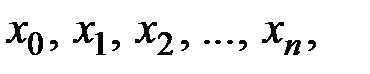 где
где 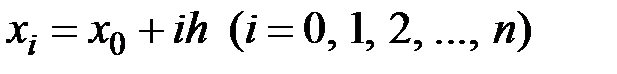 , а
, а 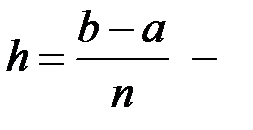 шаг интегрирования.
шаг интегрирования.
В методе Эйлера приближенные значения 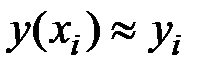 вычисляются последовательно по формуле
вычисляются последовательно по формуле
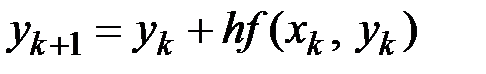
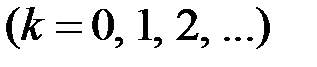 . (10.6)
. (10.6)
По методу Рунге – Кутты (см. комментарий с. 230) второго порядка точности приближенные значения вычисляются по формуле
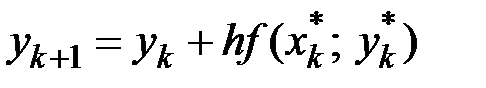 ,
,
где 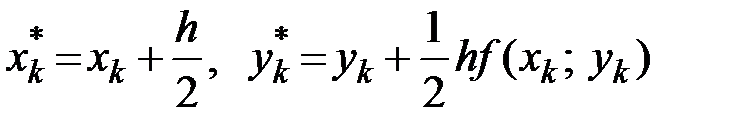 . (10.7)
. (10.7)
Задания для выполнения лабораторной работы
Задача 1. Получить численное решение дифференциального уравнения 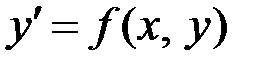 с начальным условием
с начальным условием 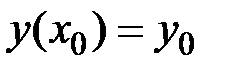 на отрезке
на отрезке 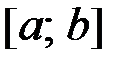 методом Эйлера. Шаг интегрирования принять равным
методом Эйлера. Шаг интегрирования принять равным 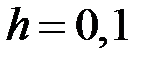
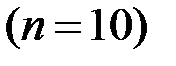 .
.
1.1. 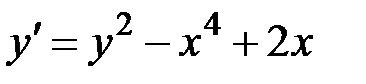 ,
, 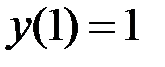 на отрезке
на отрезке 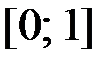 .
.
1.2. 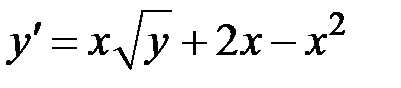 ,
, 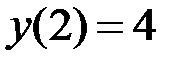 на отрезке
на отрезке 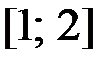 .
.
1.3. 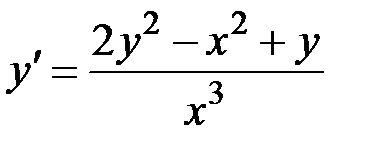 ,
, 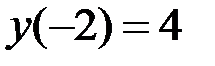 на отрезке
на отрезке 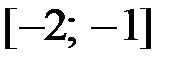 .
.
1.4. 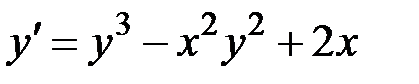 ,
, 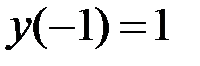 на отрезке
на отрезке 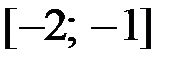 .
.
1.5. 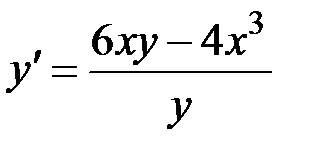 ,
, 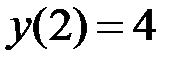 на отрезке
на отрезке 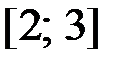 .
.
1.6. 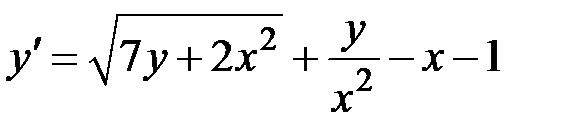 ,
, 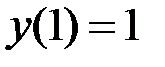 на отрезке
на отрезке 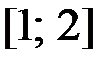 .
.
1.7. 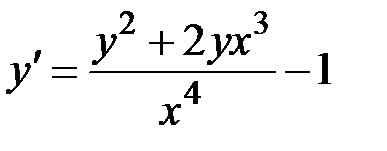 ,
, 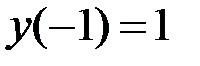 на отрезке
на отрезке 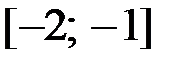 .
.
1.8. 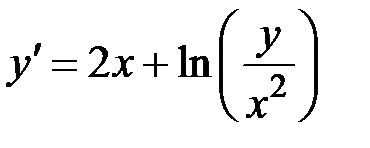 ,
, 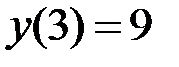 на отрезке
на отрезке 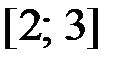 .
.
1.9. 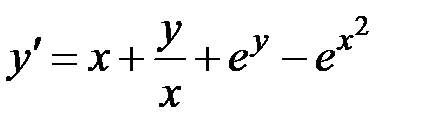 ,
, 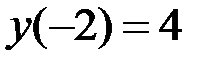 на отрезке
на отрезке 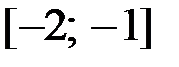 .
.
1.10. 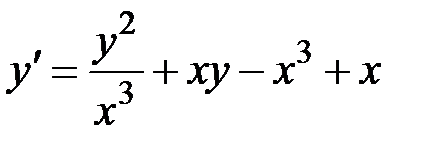 ,
, 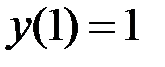 на отрезке
на отрезке 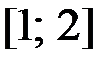 .
.
1.11. 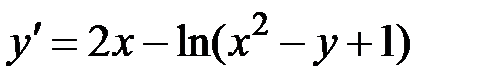 ,
, 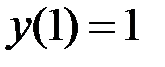 на отрезке
на отрезке 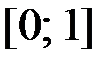 .
.
1.12. 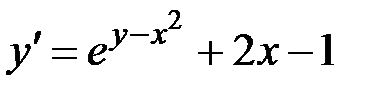 ,
, 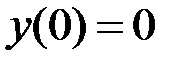 на отрезке
на отрезке 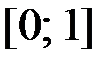 .
.
1.13. 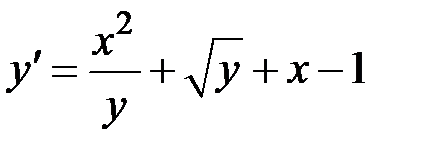 ,
, 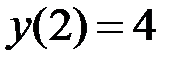 на отрезке
на отрезке 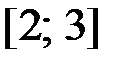 .
.
1.14. 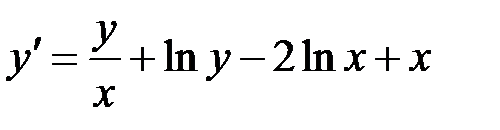 ,
, 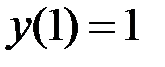 на отрезке
на отрезке 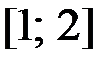 .
.
1.15. 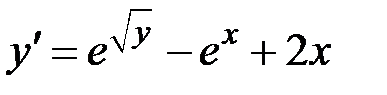
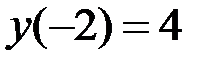 на отрезке
на отрезке 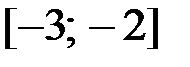 .
.
1.16. 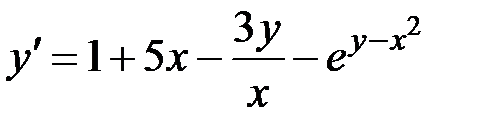 ,
, 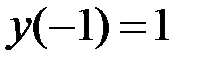 на отрезке
на отрезке 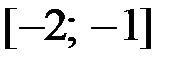 .
.
1.17. 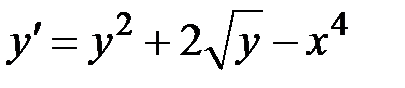 ,
, 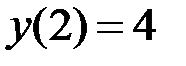 на отрезке
на отрезке 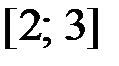 .
.
1.18. 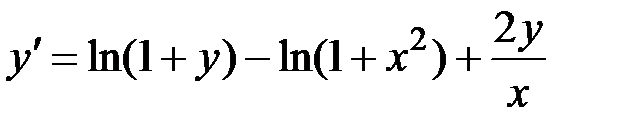 ,
, 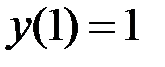 на отрезке
на отрезке 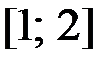 .
.
1.19. 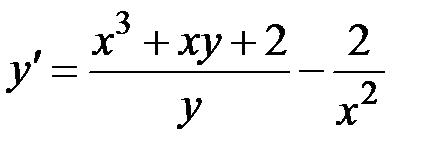 ,
, 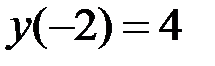 на отрезке
на отрезке 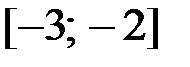 .
.
1.20. 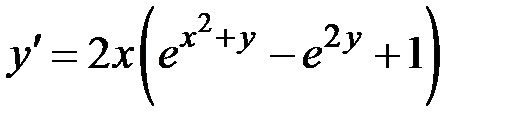 ,
, 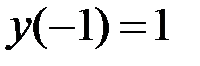 на отрезке
на отрезке 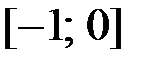 .
.
1.21. 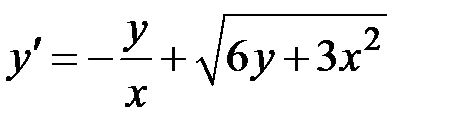 ,
, 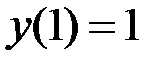 на отрезке
на отрезке 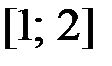 .
.
1.22. 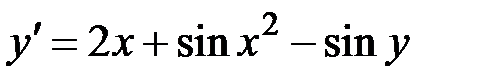 ,
, 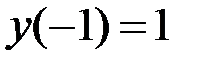 на отрезке
на отрезке 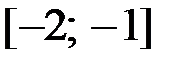 .
.
1.23. 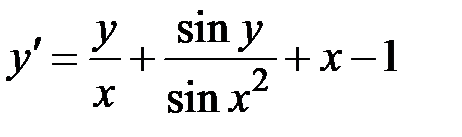 ,
, 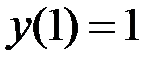 на отрезке
на отрезке 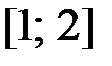 .
.
1.24. 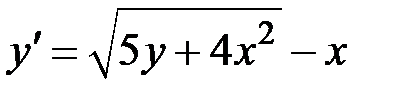 ,
, 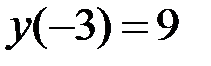 на отрезке
на отрезке 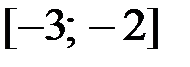 .
.
1.25. 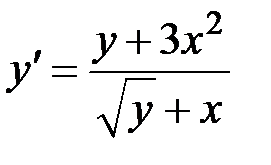 ,
, 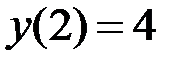 на отрезке
на отрезке 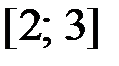 .
.
1.26. 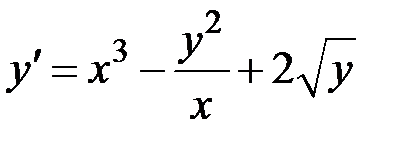 ,
, 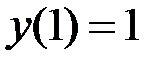 на отрезке
на отрезке 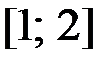 .
.
1.27. 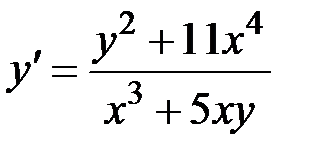 ,
, 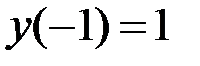 на отрезке
на отрезке 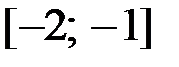 .
.
1.28. 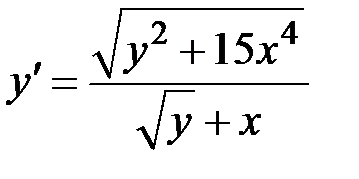 ,
, 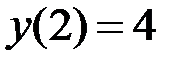 на отрезке
на отрезке 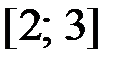 .
.
1.29. 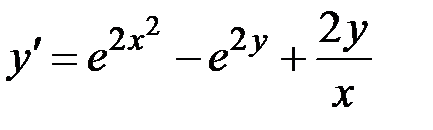 ,
, 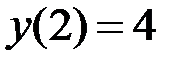 на отрезке
на отрезке 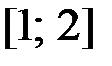 .
.
1.30. 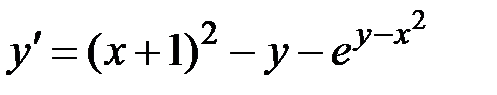 ,
, 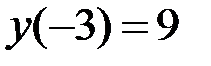 на отрезке
на отрезке 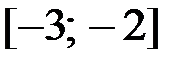 .
.
1.31. 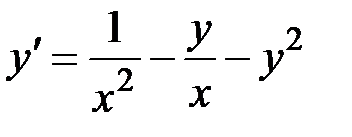 ,
, 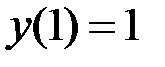 на отрезке
на отрезке 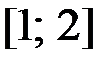 .
.
1.32. 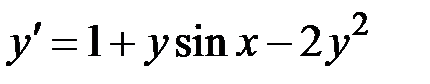 ,
, 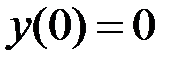 на отрезке
на отрезке 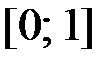 .
.
1.33. 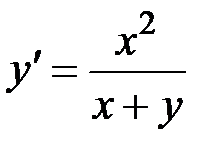 ,
, 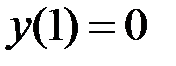 на отрезке
на отрезке 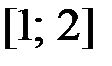 .
.
1.34. 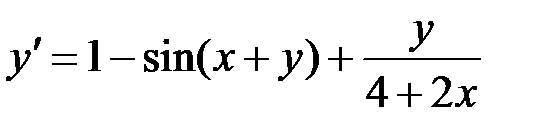 ,
, 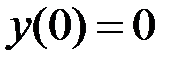 на отрезке
на отрезке 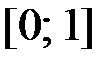 .
.
1.35. 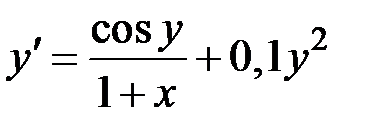 ,
, 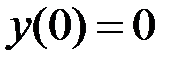 на отрезке
на отрезке 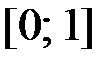 .
.
Задача 2.Получить численное решение дифференциального уравнения 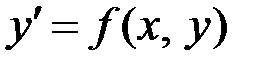 с начальным условием
с начальным условием 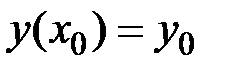 на отрезке
на отрезке 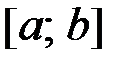 методом Рунге – Кутты, шаг интегрирования принять равным
методом Рунге – Кутты, шаг интегрирования принять равным 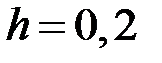
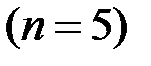 . Найти абсолютную погрешность
. Найти абсолютную погрешность 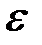 и относительную погрешность
и относительную погрешность 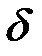 (в процентах) приближенного решения (сравнить полученный приближенный результат с точным решением при
(в процентах) приближенного решения (сравнить полученный приближенный результат с точным решением при 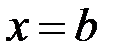 ) (варианты заданий взяты из
) (варианты заданий взяты из  ).
).
2.1. 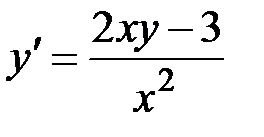 ,
, 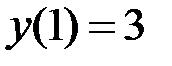 на отрезке
на отрезке 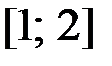 .
.
2.2. 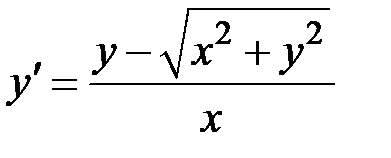 ,
, 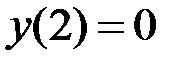 на отрезке
на отрезке 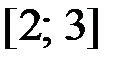 .
.
2.3. 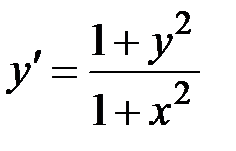 ,
, 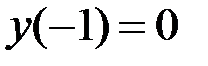 на отрезке
на отрезке 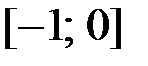 .
.
2.4. 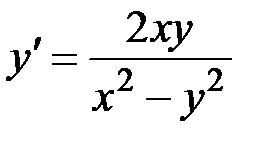 ,
, 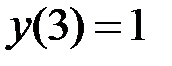 на отрезке
на отрезке 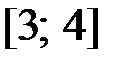 .
.
2.5. 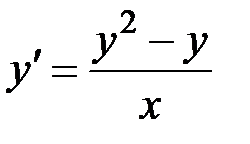 ,
, 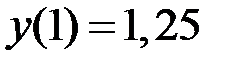 на отрезке
на отрезке 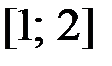 .
.
2.6. 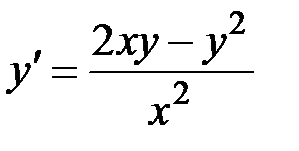 ,
, 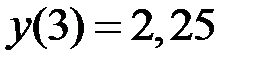 на отрезке
на отрезке 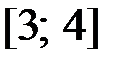 .
.
2.7. 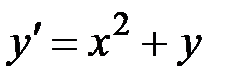 ,
, 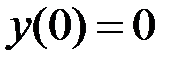 на отрезке
на отрезке 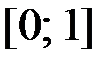 .
.
2.8. 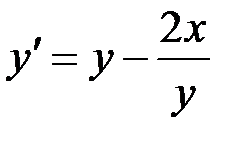 ,
, 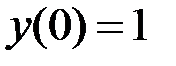 на отрезке
на отрезке 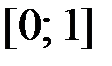 .
.
2.9. 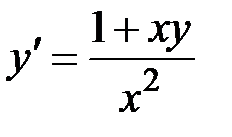 ,
, 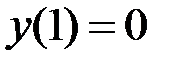 на отрезке
на отрезке 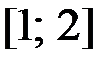 .
.
2.10. 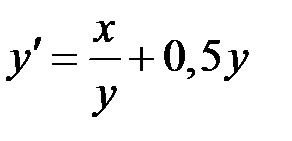 ,
, 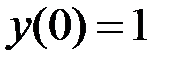 на отрезке
на отрезке 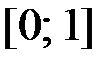 .
.
2.11. 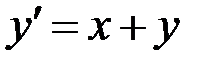 ,
, 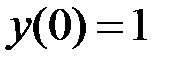 на отрезке
на отрезке 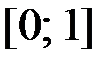 .
.
2.12. 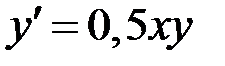 ,
, 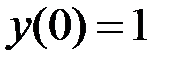 на отрезке
на отрезке 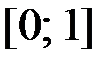 .
.
2.13. 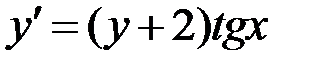 ,
, 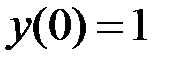 на отрезке
на отрезке 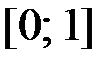 .
.
2.14. 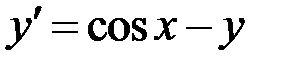 ,
, 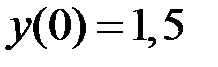 на отрезке
на отрезке 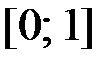 .
.
2.15. 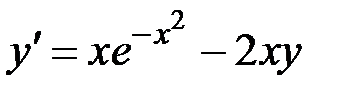 ,
, 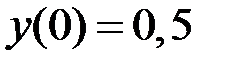 на отрезке
на отрезке 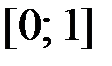 .
.
2.16. 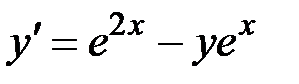 ,
, 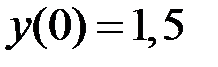 на отрезке
на отрезке 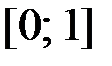 .
.
2.17. 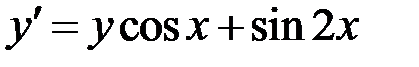 при
при 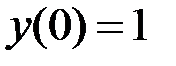 на отрезке
на отрезке 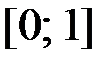 .
.
2.18. 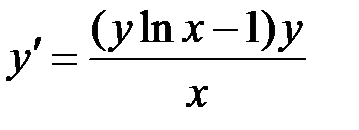 ,
, 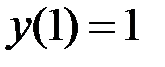 на отрезке
на отрезке 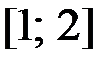 .
.
2.19. 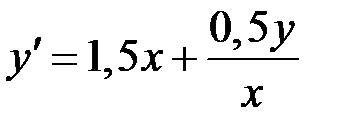 ,
, 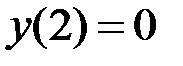 на отрезке
на отрезке 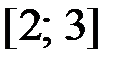 .
.
2.20. 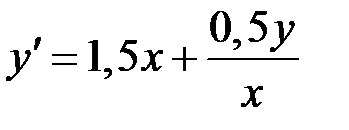 ,
, 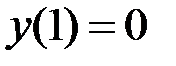 на отрезке
на отрезке 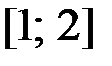 .
.
2.21. 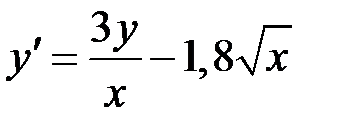 ,
, 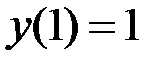 на отрезке
на отрезке 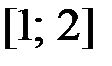 .
.
2.22. 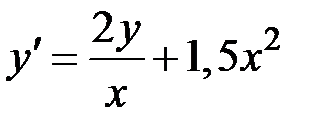 ,
, 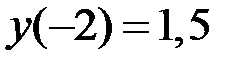 на отрезке
на отрезке 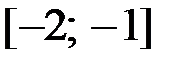 .
.
2.23. 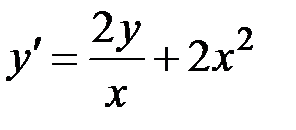 ,
, 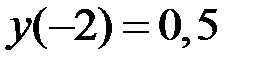 на отрезке
на отрезке 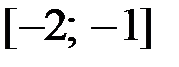 .
.
2.24. 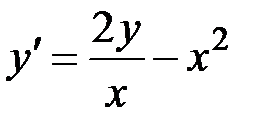 ,
, 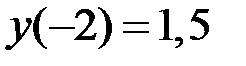 на отрезке
на отрезке 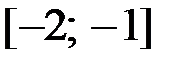 .
.
2.25. 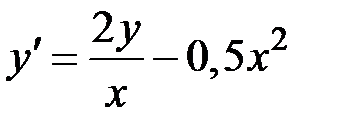 ,
, 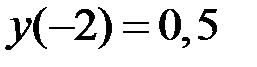 на отрезке
на отрезке 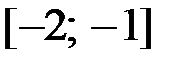 .
.
2.26. 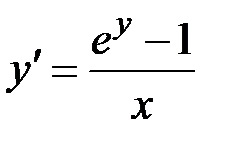 ,
, 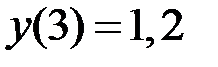 на отрезке
на отрезке 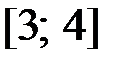 .
.
2.27. 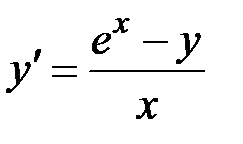 ,
, 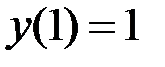 на отрезке
на отрезке 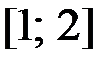 .
.
2.28. 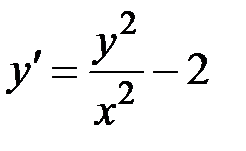 ,
, 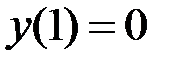 на отрезке
на отрезке 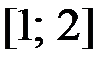 .
.
2.29. 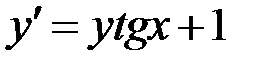 ,
, 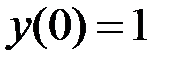 на отрезке
на отрезке 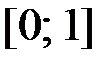 .
.
2.30. 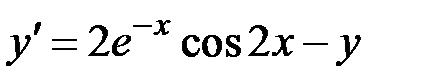 ,
, 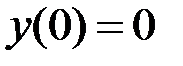 на отрезке
на отрезке 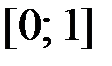 .
.
Решение типовых задач
Пример 1. Получить численное решение дифференциального уравнения 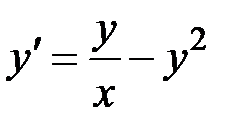 с начальным условием
с начальным условием 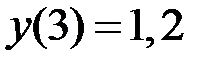 на отрезке
на отрезке 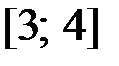 с шагом
с шагом 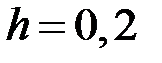
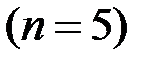 , используя методы Эйлера и Рунге – Кутты. Найти погрешности полученных приближенных решений, сравнив их с точным решением (пример из
, используя методы Эйлера и Рунге – Кутты. Найти погрешности полученных приближенных решений, сравнив их с точным решением (пример из  ).
).
 Данное уравнение является уравнением Бернулли, его частное решение имеет вид
Данное уравнение является уравнением Бернулли, его частное решение имеет вид 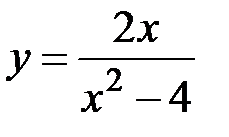 . Тогда точное значение
. Тогда точное значение 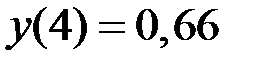 .
.
В задаче даны 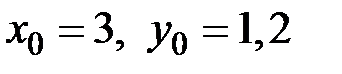 ,
, 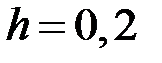 . Используя расчетную формулу (10.6) метода Эйлера заполняем таблицу 10.2
. Используя расчетную формулу (10.6) метода Эйлера заполняем таблицу 10.2
Таблица 10.2
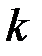 | 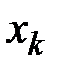 | 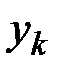 | 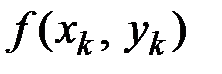 | 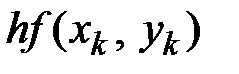 |
| 3,0 | 1,2 | – 1,04 | – 0,208 | |
| 3,2 | 0,992 | – 0,67406 | – 0,13481 | |
| 3,4 | 0,85719 | – 0,48266 | – 0,09653 | |
| 3,6 | 0,76066 | – 0,36731 | – 0,07346 | |
| 3,8 | 0,68720 | – 0,29140 | – 0,05828 | |
| 4,0 | 0,62892 |
Используя расчетные формулы метода Рунге – Кутты (10.7) заполняем таблицу 10.3.
Таблица 10.3
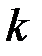 | 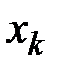 | 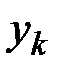 | 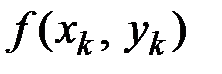 | 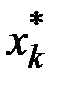 | 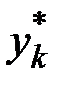 | 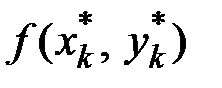 | 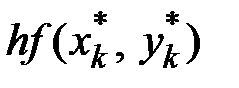 |
| 3,0 | 1,2 | – 1,04 | 3,1 | 1,096 | – 0,84765 | – 0,16953 | |
| 3,2 | 1,03047 | – 0,73905 | 3,3 | 0,95649 | – 0,62503 | – 0,12501 | |
| 3,4 | 0,90547 | – 0,55356 | 3,5 | 0,85011 | – 0,47980 | – 0,09596 | |
| 3,6 | 0,80951 | – 0,43044 | 3,7 | 0,76647 | – 0,38320 | – 0,07606 | |
| 3,8 | 0,73345 | – 0,34494 | 3,9 | 0,69895 | – 0,30932 | – 0,06186 | |
| 4,0 | 0,67158 |
Погрешности (абсолютная 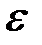 и относительная
и относительная 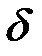 ) приближенных значений
) приближенных значений 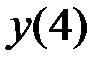 приведены в таблице 10.4.
приведены в таблице 10.4.
Таблица 10.4
| Решение | 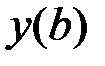 | 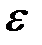 | 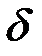 , % , % |
| точное | 0,66667 | – | – |
| приближенное методом Эйлера | 0,62892 | 0,0377 | 5,7 |
| приближенное методом Рунге – Кутты | 0,67158 | 0,0049 | 0,7 |

Контрольные задания по теме «Дифференциальные уравнения»
1. Доказать, что решением уравнения первого порядка 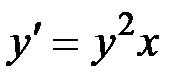 является функция
является функция 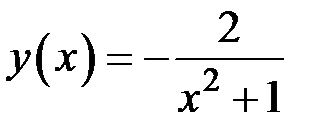 .
.
2. Определить типы дифференциальных уравнений 1-го порядка:
1) 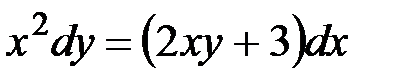 , 2)
, 2) 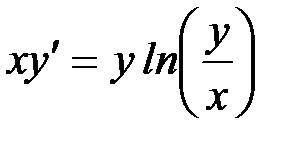 , 3)
, 3) 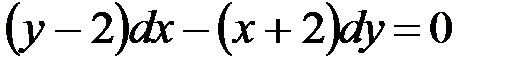 ,
,
4) 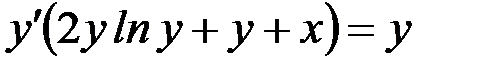 , 5)
, 5) 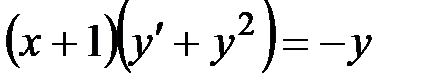 .
.
3. Найти общее решение уравнения 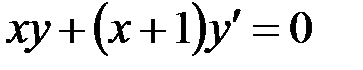 .
.
4. Найти общее решение дифференциального уравнения 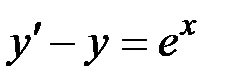 .
.
5. Найти 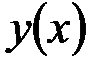 – решение задачи Коши:
– решение задачи Коши: 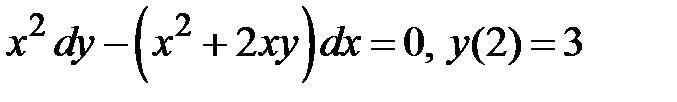 .
.
6. Найти общее решение дифференциального уравнения 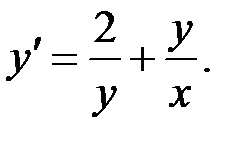
7. Найти общее решение 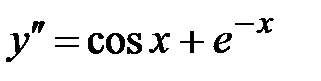 .
.
8. Проверить, какая из следующих функций является решением уравнения 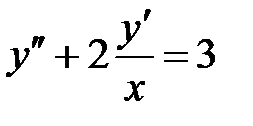 : 1)
: 1) 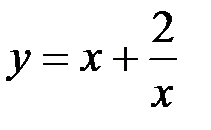 , 2)
, 2) 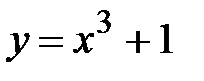 , 3)
, 3) 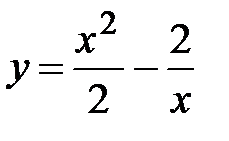 , 4)
, 4) 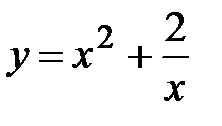 .
.
9.Записать линейное однородное дифференциальное уравнение второго порядка относительно искомой функции 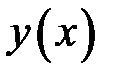 , если известны корни его характеристического уравнения:
, если известны корни его характеристического уравнения: 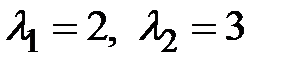 .
.
10. Найти решение задачи Коши: 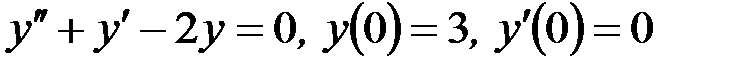 .
.
11. Найти вид частного решения следующих линейных неоднородных дифференциальных уравнений, не вычисляя неопределенных коэффициентов:
1) 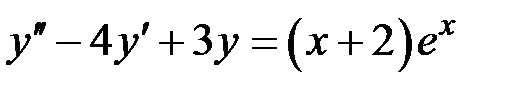 , 2)
, 2)  ,
,
3) 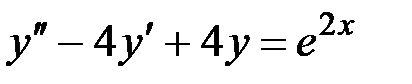 , 4)
, 4) 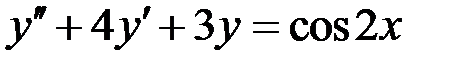 .
.
12. Найти общее решение дифференциального уравнения 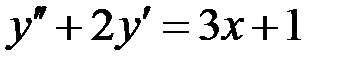 .
.
