Уравнение в полных дифференциалах
Интегрирование уравнения в полных дифференциалах
Выражение
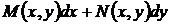
называется полным дифференциалом, если существует такая функция 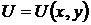 , что справедливо тождество
, что справедливо тождество
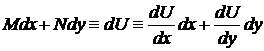 .
.
Последнее тождество равносильно двум следующим
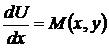 ,
, 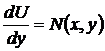 . (43)
. (43)
В частном случае, когда левая часть дифференциального уравнения
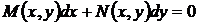 (7)
(7)
представляет полный дифференциал некоторой функции 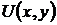 (для которой выполняются равенства (43), то говорят, что задано уравнение в полных (точных) дифференциалах и, следовательно, уравнение (7) принимает вид
(для которой выполняются равенства (43), то говорят, что задано уравнение в полных (точных) дифференциалах и, следовательно, уравнение (7) принимает вид
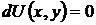 .
.
Если функция 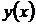 является решение уравнения (7), то
является решение уравнения (7), то
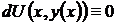 , отсюда
, отсюда 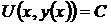 , (44)
, (44)
где С – постоянная, и наоборот, если некоторая функция 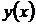 обращает в тождество (конечное) уравнение (44), то дифференцируя полученное тождество, получим
обращает в тождество (конечное) уравнение (44), то дифференцируя полученное тождество, получим 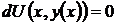 . Следовательно, выражение
. Следовательно, выражение
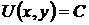 , (44)
, (44)
где С – произвольная постоянная, суть общий интеграл уравнения (7). Его левая часть, т.е. функция 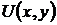 , является интегралом уравнения (7) в рассматриваемом частном случае.
, является интегралом уравнения (7) в рассматриваемом частном случае.
Некоторые элементарные уравнения в точных дифференциалах удается легко проинтегрировать приведением к виду 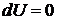 , обходясь без квадратур и ограничиваясь лишь непосредственной группировкой их членов. Такой подход является аналогом известного в математическом анализе метода непосредственного интегрирования («внесением под знак дифференциала», только более сложным). Однако, в общем случае, уже при рассмотрении уравнения (7), возникает вопрос о самой принадлежности этого уравнения к классу уравнений в точных дифференциалах.
, обходясь без квадратур и ограничиваясь лишь непосредственной группировкой их членов. Такой подход является аналогом известного в математическом анализе метода непосредственного интегрирования («внесением под знак дифференциала», только более сложным). Однако, в общем случае, уже при рассмотрении уравнения (7), возникает вопрос о самой принадлежности этого уравнения к классу уравнений в точных дифференциалах.
Пусть функции 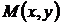 и
и 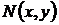 определены и непрерывны вместе со своими первыми производными в некоторой односвязной области G. Тогда, для того чтобы уравнение (7) было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось условие
определены и непрерывны вместе со своими первыми производными в некоторой односвязной области G. Тогда, для того чтобы уравнение (7) было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось условие
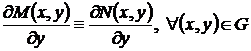 , (45)
, (45)
которое впервые получил Леонард Эйлер.
Необходимость. Если уравнение (7) в точных дифференциалах, то, согласно равенствам (43) и известной теореме из математического анализа: «результат дифференцирования не зависит от порядка, в котором производится дифференцирование, если соответствующие производные непрерывны»,
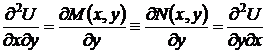 .
.
Достаточность. Предположим, что условие (45) выполнено. Найдем функцию 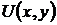 , удовлетворяющую соотношениям (43). Пусть в точке
, удовлетворяющую соотношениям (43). Пусть в точке 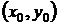 функции
функции 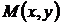 и
и 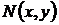 не обращаются одновременно в нуль. Интегрируя по переменной х в пределах от х0 до х левое из соотношений (43) и считая у постоянной, получаем
не обращаются одновременно в нуль. Интегрируя по переменной х в пределах от х0 до х левое из соотношений (43) и считая у постоянной, получаем
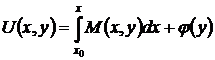 , (46)
, (46)
где 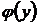 произвольная функция. Выберем функцию
произвольная функция. Выберем функцию 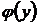 так, чтобы выполнялось и второе (правое) соотношение (43). Для этого продифференцируем обе части равенства (46) по у, применяя правило дифференцирования интеграла по параметру («правило Лейбница»),
так, чтобы выполнялось и второе (правое) соотношение (43). Для этого продифференцируем обе части равенства (46) по у, применяя правило дифференцирования интеграла по параметру («правило Лейбница»),
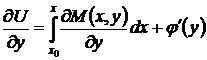 .
.
Заменим подынтегральную функцию, используя условие (45), и затем вычислим интеграл
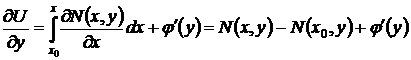 .
.
Видно, что правая часть полученного выражения окажется в точности равной функции 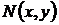 , если положить
, если положить
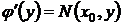 , отсюда
, отсюда 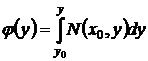 .
.
Таким образом, функция 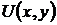 найдена
найдена
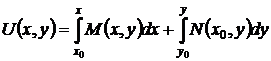
и общий интеграл (44) уравнения в полных дифференциалах (7) принимает вид
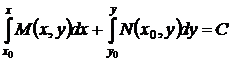 , (47)
, (47)
или, в силу очевидной симметрии
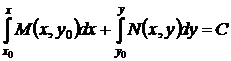 . (48)
. (48)
Из курса математического анализа известно, что криволинейный интеграл от точного дифференциала некоторой однозначной функции по замкнутому контуру, целиком лежащему в односвязной области (т.е. стягивающемуся в точку), равен нулю. Поэтому, если выполняется условие Эйлера (5), проще проинтегрировать уравнение (7), взяв криволинейный интеграл второго типа (криволинейный интеграл по координатам) от обеих частей уравнения (7) между некоторой фиксированной точки 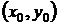 и «подвижной» точкой
и «подвижной» точкой 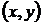 по любому пути, получив таким образом решение задачи Коши в виде интеграла уравнения (7)
по любому пути, получив таким образом решение задачи Коши в виде интеграла уравнения (7)
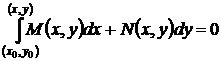 . (49)
. (49)
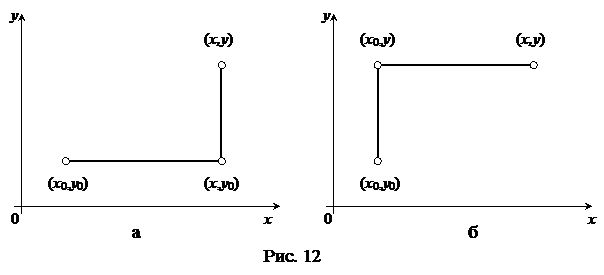 |
В качестве пути интегрирования удобно брать ломаную, составленную из двух звеньев, параллельным осям (рис. 12), тогда:
а) 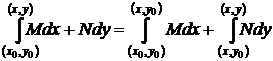 ;
;
б) 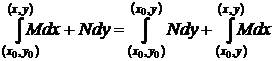 .
.
Заметим, что решение задачи Коши можно получить, полагая С = 0 в равенствах (47) или (48), которое может быть представлено либо в виде 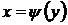 в окрестности точки
в окрестности точки 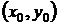 , согласно теории неявных функций.
, согласно теории неявных функций.
Интегрирующий множитель. В некоторых случаях, когда уравнение (7) не является уравнением в полных дифференциалах, удается подобрать функцию 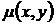 , после умножения на которую, левая часть уравнения (7) превращается в полный дифференциал
, после умножения на которую, левая часть уравнения (7) превращается в полный дифференциал
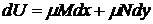 .
.
Такая функция 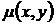 называется интегрирующим множителем.
называется интегрирующим множителем.
По определению интегрирующего множителя имеем
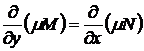 ,
,
или
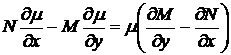 ,
,
откуда, деля обе части равенства на 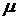 , получаем уравнение в частных производных относительно неизвестной функции
, получаем уравнение в частных производных относительно неизвестной функции 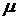
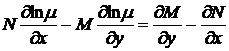 . (50)
. (50)
В общем случае интегрирование этого уравнения является задачей более трудной, чем интегрирование исходного уравнения, однако в некоторых случаях подбор решения уравнения (50) сравнительно прост в осуществлении.
Считая, что интегрирующий множитель является функцией только одного аргумента (например, 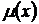 ,
, 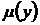 ,
, 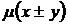 ,
, 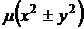 ,
, 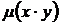 ,
, 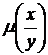 и т.д.), можно уже без труда проинтегрировать уравнение (50) и указать условия, при которых интегрирующий множитель рассматриваемого вида существует. Тем самым выделяются классы уравнений, для которых интегрирующий множитель может быть найден. Рассмотрим два частных случая.
и т.д.), можно уже без труда проинтегрировать уравнение (50) и указать условия, при которых интегрирующий множитель рассматриваемого вида существует. Тем самым выделяются классы уравнений, для которых интегрирующий множитель может быть найден. Рассмотрим два частных случая.
1. Если 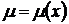 , то уравнение (50) примет вид
, то уравнение (50) примет вид
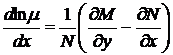 ,
, 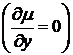 . (51)
. (51)
Для существования интегрирующего множителя необходимо и достаточно, чтобы правая часть уравнения (51) была функцией только х, тогда ln 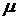 найдется квадратурой.
найдется квадратурой.
2. Аналогично, если выражение
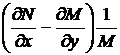
есть функция только у, то уравнение (7) имеет интегрирующий множитель 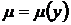 .
.
Если функции M и N имеют непрерывные производные в области G и по крайней мере одна из этих функций не обращается в нуль, можно доказать существование ненулевого решения уравнения в частных производных (50), или, что то же самое, существование интегрирующего множителя. Следовательно, метод интегрирующего множителя (развитый еще в работах Эйлера) можно рассматривать как общий метод интегрирования уравнений (7). Однако, ввиду трудности нахождения интегрирующего множителя этот метод применяется лишь в тех случаях, когда интегрирующий множитель очевиден.
Примеры.
30. 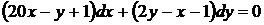 . Это уравнение в полных дифференциалах, поскольку удовлетворяется условие (45). Группируя, находим
. Это уравнение в полных дифференциалах, поскольку удовлетворяется условие (45). Группируя, находим
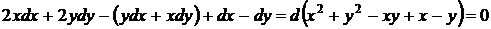 ,
,
следовательно, общий интеграл данного уравнения
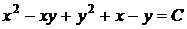 .
.
31. 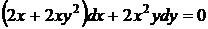 . Здесь не следует сокращать на
. Здесь не следует сокращать на 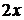 , так как после сокращения левая часть перестает быть полным дифференциалом. Группируя
, так как после сокращения левая часть перестает быть полным дифференциалом. Группируя
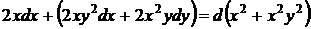 ,
,
согласно формуле (44), находим общий интеграл
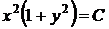 .
.
32. Найти решение задачи Коши:
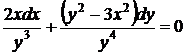 ,
, 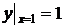 .
.
Здесь 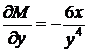 ,
, 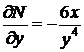 , так что условие (45) выполнено, поэтому данное уравнение есть уравнение в полных дифференциалах. Замечая, что
, так что условие (45) выполнено, поэтому данное уравнение есть уравнение в полных дифференциалах. Замечая, что
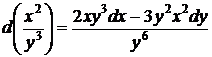 ,
, 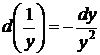 ,
,
непосредственной группировкой членов уравнения находим общий интеграл (44) данного уравнения
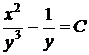 .
.
Используя начальные условия, определяем, что 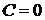 , следовательно, решение поставленной задачи Коши
, следовательно, решение поставленной задачи Коши
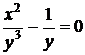 или
или 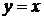 .
.
33. 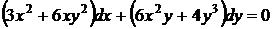 . Здесь
. Здесь
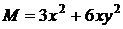 ,
, 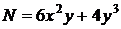 ,
, 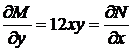 .
.
Вместо применения формул (47) или (48), на практике часто оказывается проще дифференцировать равенство (46) по у и, заменяя 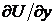 известной функцией
известной функцией 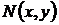 , определить из полученного выражения
, определить из полученного выражения 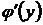 , а затем найти
, а затем найти 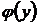 квадратурой.
квадратурой.
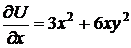 ,
, 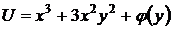 ;
;
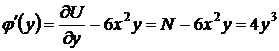 ,
, 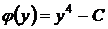 .
.
Итак, общий интеграл 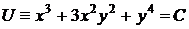 .
.
34. Найти решение задачи Коши:
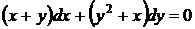 ,
, 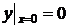 .
.
Условие (45) выполнено во всей плоскости, поэтому для любой точки 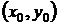 формулы (47) или (48) при
формулы (47) или (48) при 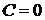 доставляют решение задачи Коши в неявном виде
доставляют решение задачи Коши в неявном виде
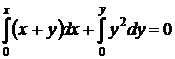 , или
, или 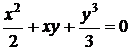 .
.
35. Найти решение задачи Коши:
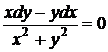 ,
, 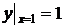 .
.
Здесь условие (45) выполнено во всей плоскости с выключенной точкой (0,0), т.е. в двусвязной области. Известно, что в случае многосвязной области 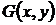 функция
функция 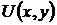 (левая часть уравнения (49)) также определена во всей области
(левая часть уравнения (49)) также определена во всей области 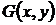 , но может оказаться многозначной. В этом случае можно получать решения задачи Коши при помощи формулы (49) так же, как и при помощи формулы (47) поскольку в односвязной части
, но может оказаться многозначной. В этом случае можно получать решения задачи Коши при помощи формулы (49) так же, как и при помощи формулы (47) поскольку в односвязной части 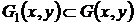 любая ветвь функции
любая ветвь функции 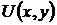 удовлетворяет равенству dU = 0. Значения любой ветви функции
удовлетворяет равенству dU = 0. Значения любой ветви функции 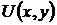 в односвязной части
в односвязной части 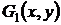 области
области 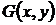 отличаются от значений другой ветви, построенной в этой области
отличаются от значений другой ветви, построенной в этой области 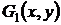 , на постоянное число. Именно поэтому следует свойство dU = 0 в случае многосвязной области
, на постоянное число. Именно поэтому следует свойство dU = 0 в случае многосвязной области 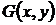 , поскольку условие (45) не является достаточным в этом случае.
, поскольку условие (45) не является достаточным в этом случае.
Применяя формулу (49) в варианте б, как показано на рис. 12, найдем интеграл рассматриваемого уравнения
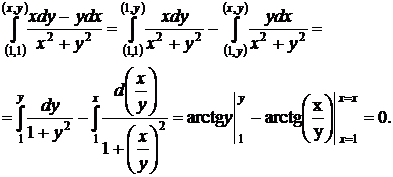
Используя формулу сложения для обратных тригонометрических функций
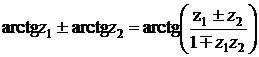 ,
,
из интеграла находим решение поставленной задачи Коши
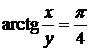 , или
, или 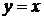 .
.
36. Найти интеграл уравнения
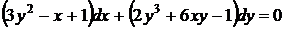 .
.
Применяя формулу (49) в варианте а (рис. 12) и полагая 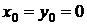 , найдем интеграл данного уравнения.
, найдем интеграл данного уравнения.
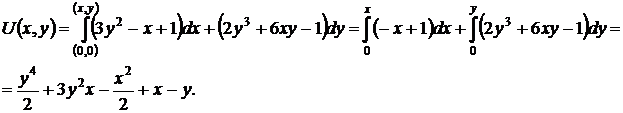
37. 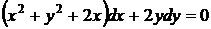 . Данное уравнение не является уравнением в полных дифференциалах, но, составляя уравнение для интегрирующего множителя (50), можно заметить, что выполняется частный случай 1.(51) этого уравнения.
. Данное уравнение не является уравнением в полных дифференциалах, но, составляя уравнение для интегрирующего множителя (50), можно заметить, что выполняется частный случай 1.(51) этого уравнения.
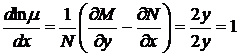 ,
, 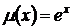 .
.
Умножением на интегрирующий множитель 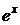 приводим рассматриваемое уравнение к уравнению в полных дифференциалах.
приводим рассматриваемое уравнение к уравнению в полных дифференциалах.
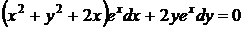 .
.
Показанным в примере 33 способом
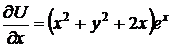 ,
, 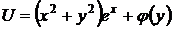 ,
,
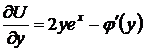 ,
, 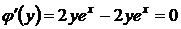 ,
,
находим общий интеграл данного уравнения
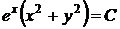 .
.
38. 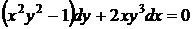 . Здесь для уравнения (50) выполняется частный случай 2.
. Здесь для уравнения (50) выполняется частный случай 2.
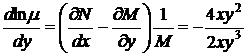 ,
, 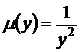 .
.
Соответствующее уравнение в полных дифференциалах имеет вид
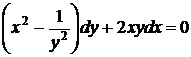 .
.
Полагая 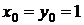 , применим формулу (49) (рис. 12, б)
, применим формулу (49) (рис. 12, б)
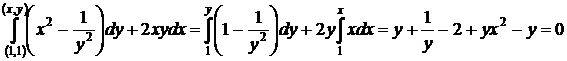 ,
,
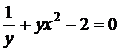 ;
;
следовательно, общий интеграл рассматриваемого уравнения
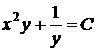 .
.
Пусть для уравнения (7) 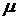 есть какой-нибудь интересующий множитель, а
есть какой-нибудь интересующий множитель, а 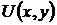 есть интеграл этого уравнения. Тогда при произвольной дифференцируемой функции
есть интеграл этого уравнения. Тогда при произвольной дифференцируемой функции 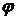 величина
величина
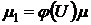 (52)
(52)
является также интегрирующим множителем уравнения (7).
Данное утверждение воплощается на практике в виде технического приема, когда члены исследуемого уравнения разбиваются на (две) группы, для каждой из которых легко усмотреть интегрирующий множитель (и интеграл). Затем из выражений (52) для интегрирующего множителя каждой группы выбираются подходящие произвольные функции с тем, чтобы интегрирующие множители групп оказались равными (согласованными).
39. 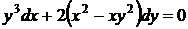 . Проинтегрируем это уравнение методом интегрирующего множителя Эйлера. Для нахождения множителя разобьем уравнение на две группы
. Проинтегрируем это уравнение методом интегрирующего множителя Эйлера. Для нахождения множителя разобьем уравнение на две группы
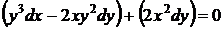 .
.
Замечая, что разделение переменных сводится к умножению на некоторый интегрирующий множитель, определяем интегрирующий множитель первой скобки и интеграл
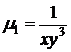 ,
, 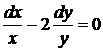 ,
, 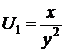 ;
;
у второй скобки очевиден интегрирующий множитель 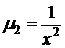 . Общее выражение интегрирующего множителя первой скобки, согласно формуле (52), имеет вид
. Общее выражение интегрирующего множителя первой скобки, согласно формуле (52), имеет вид
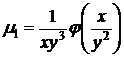 .
.
Выберем теперь произвольную функцию 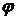 так, чтобы множитель
так, чтобы множитель 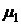 по переменной х совпадал бы с
по переменной х совпадал бы с 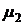 . Для этого достаточно положить
. Для этого достаточно положить 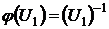 и получить
и получить
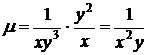 .
.
Умножая исходное уравнение на 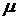 , приводим его к уравнению в точных дифференциалах
, приводим его к уравнению в точных дифференциалах
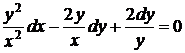 ,
,
откуда немедленно следует общий интеграл
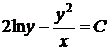 .
.
40. 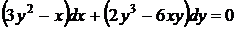 . Группируя члены данного уравнения, можно увидеть
. Группируя члены данного уравнения, можно увидеть  и
и 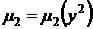 для отдельных групп. Однако определить сразу общий для всего уравнения интегрирующий множитель
для отдельных групп. Однако определить сразу общий для всего уравнения интегрирующий множитель 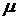 не удается, поэтому обратимся к уравнению (50).
не удается, поэтому обратимся к уравнению (50).
Предположим 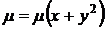 ,
, 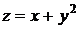 ,
, 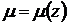 , тогда
, тогда
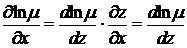 ,
, 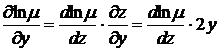 .
.
Уравнение (50) принимает вид
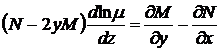 ,
, 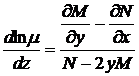 .
.
Для данного уравнения 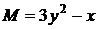 ,
, 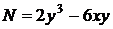 , значит
, значит
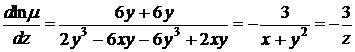 ,
,
отсюда находим интегрирующий множитель 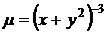 , следовательно, данное уравнение приводится к уравнению в полных дифференциалах
, следовательно, данное уравнение приводится к уравнению в полных дифференциалах
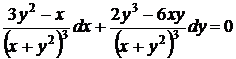 ,
,
поскольку
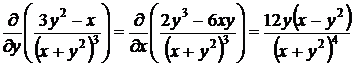 .
.
Методом, изложенным в примерах 33, 37, проинтегрируем полученное уравнение
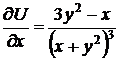 ;
; 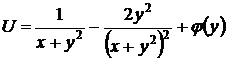 ;
;
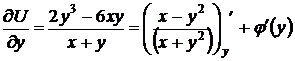 ;
; 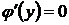 ;
;
таким образом, запишем общий интеграл исходного уравнения
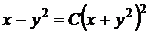 .
.
Линейное уравнение
Линейным дифференциальным уравнением первого порядка неоднородным называется уравнение, линейное относительно неизвестной функции и ее производной. Оно имеет вид
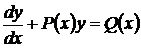 , (53)
, (53)
где заданные функции 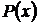 и
и 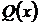 определены и непрерывны в интервале
определены и непрерывны в интервале 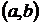 . Наряду с неоднородным рассматривается линейное однородное уравнение.
. Наряду с неоднородным рассматривается линейное однородное уравнение.
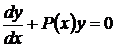 . (54)
. (54)
Всякое решение линейного уравнения есть частное решение, особых решений линейное уравнение не имеет, поскольку в области
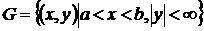
всегда выполняются условия существования и единственности решения задачи Коши для линейного уравнения с непрерывными коэффициентами P, Q (53).
Методы интегрирования линейного уравнения
1. Метод мультипликативной подстановки Бернулли. Мультипликативная подстановка (34), предложенная в 1693г. Лейбницем для интегрирования однородного уравнения была обобщена его ближайшими последователями, братьями Бернулли (и самим Г.В. Лейбницем) в работах 1696–1697гг. на случай линейного уравнения в виде
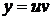 ,
, 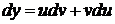 , (55)
, (55)
где 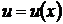 и
и 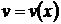 некоторые неизвестные функции.
некоторые неизвестные функции.
Следуя методу, запишем уравнение (53) и дифференциалах и применим подстановку(55)
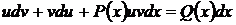 .
.
Считая, например, функцию v неизвестной, а функцию u произвольной, сгруппируем второй и третий члены в левой части вышенаписанного равенства
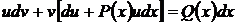 . (56)
. (56)
Выберем функцию и так, чтобы выражение в квадратных скобках уравнения (56) обращалось в нуль
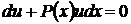 . (54)
. (54)
Это линейное однородное уравнение относительно неизвестной функции и является также уравнением с разделяющимися переменными. Разделяя переменные, квадратурой, потенцируя
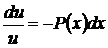 ,
, 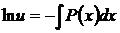 ,
,
находим искомую функцию
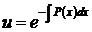 . (57)
. (57)
Постоянную интегрирования здесь не пишем, так как достаточно в качестве функции 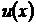 взять какое-нибудь отличное от нуля частное решение уравнения (54).
взять какое-нибудь отличное от нуля частное решение уравнения (54).
Подставим найденную функцию (57) в уравнение (56). Так как в этом уравнении выражение в квадратных скобках равно нулю, получим уравнение с разделяющимися переменными v и х
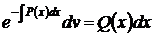
Разделяя переменные, квадратурой, находим вторую искомую функцию
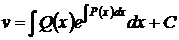 . (58)
. (58)
Возвращая выражения (57) и (58), соответственно для функций u и v, в подстановку (55), получаем общее решение уравнения (53) в рассматриваемой области G
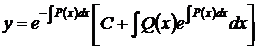 . (59)
. (59)
Его можно переписать в форме Коши
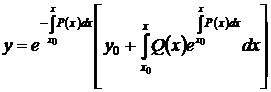 . (60)
. (60)
Из формулы (60) видно, что всякое решение однородного уравнения является непрерывно дифференцируемой функцией как зависимой переменной х, так и начальных данных х0 и у0.
2. Метод интегрирующего множителя Эйлера. Особенно широкое развитие метод интегрирующего множителя получил в работах Эйлера 1768–1769гг., в которых был установлен ряд классов дифференциальных уравнений первого порядка, обладающих множителем данного вида.
Для линейного уравнения (53) выполнено условие существования интегрирующего множителя, зависящего только от х. В самом деле (проверим условие 1 формула (50))
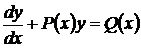 ,
, 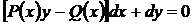 ,
,
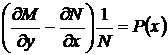 , следовательно
, следовательно 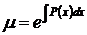 .
.
Следуя методу, умножим обе части уравнения (53) на интегрирующий множитель, найденный выше
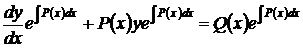 .
.
Так как левая часть этого равенства представляет собой производную произведения, то
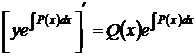 ,
,
или в полных дифференциалах
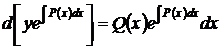 .
.
Интегрируя последнее равенство, получаем
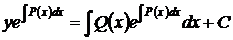 ,
,
откуда искомое общее решение уравнения (53)
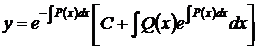 . (59)
. (59)
3. Метод вариации произвольной постоянной Лагранжа. Этот метод был детально разработан Лагранжем в 1766–1777гг.
Обратимся к линейному однородному уравнению (54)
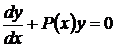 . (54)
. (54)
Из формулы (54) видно, что однородное линейное уравнение всегда имеет тривиальное нулевое решение 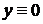 , которое не представляет практического интереса, хотя является одним из частных решений. В области G нетрудно получить общее решение уравнения (54) в виде
, которое не представляет практического интереса, хотя является одним из частных решений. В области G нетрудно получить общее решение уравнения (54) в виде
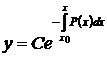 ,
, 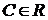 (60)
(60)
или в форме Коши
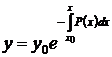 . (61)
. (61)
Все решения однородного линейного уравнения (54) содержатся в формуле общего решения (60) или (61). Любое ненулевое решение однородного линейного уравнения целиком расположено или выше или ниже оси Ох. Если у1 – ненулевое решение уравнения (54), то 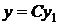 есть общее решение этого уравнения.
есть общее решение этого уравнения.
Следуя методу, зная решение однородного уравнения (54), будем искать общее решение неоднородного уравнения (53) в виде
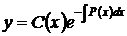 , (62)
, (62)
где 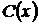 – некоторая непрерывно дифференцируемая функция х. Для определения функции
– некоторая непрерывно дифференцируемая функция х. Для определения функции 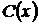 подставим выражение (62) в данное неоднородное уравнение (53) (по сути осуществим замену специального вида (62) неизвестной функции у), предварительно вычисляя производную
подставим выражение (62) в данное неоднородное уравнение (53) (по сути осуществим замену специального вида (62) неизвестной функции у), предварительно вычисляя производную
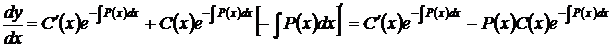 .
.
После подстановки и приведения подобных, приходим к дифференциальному уравнению с разделяющимися переменными С и х
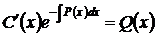 .
.
Интегрируя, получаем
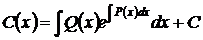 ,
,
здесь новая произвольная постоянная снова обозначена через С. В результате подстановки полученного значения 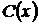 в равенство (62), находим общее решение данного неоднородного линейного уравнения
в равенство (62), находим общее решение данного неоднородного линейного уравнения
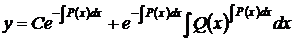 , (63)
, (63)
которое совпадает с решением (59). Из вида (63) следует важное предложение. Общее решение линейного неоднородного дифференциального уравнения (53) равно сумме общего решения соответствующего однородного уравнения (60) и частного решения неоднородного уравнения,получающегося, например, из формулы (63) при 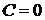 .
.
Заметим, что при практическом рассмотрении конкретных примеров не рационально пользоваться готовыми формулами (59), (63). Важно владеть методами их получения.
Примеры.
41. 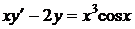 . Это линейное уравнение, будем искать его общее решение методом Бернулли в виде (55)
. Это линейное уравнение, будем искать его общее решение методом Бернулли в виде (55)
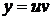 ,
, 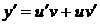 .
.
Подставим выражения для у и у' в данное уравнение и перегруппируем его, выделив квадратными скобками условие для нахождения первой искомой функции 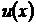
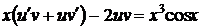 ,
,
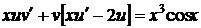 .
.
Из условия 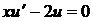 , разделяя переменные, квадратурой получаем
, разделяя переменные, квадратурой получаем
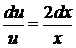 ,
, 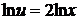 ,
, 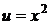 ;
;
здесь не пишем константу интегрирования, так как достаточно любого частного решения при нахождении первой функции. Подставляя частное решение 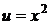 в промежуточное уравнение, с учетом того, что выражение в квадратных скобках обращается в нуль, приходим к уравнению для определения второй искомой функции
в промежуточное уравнение, с учетом того, что выражение в квадратных скобках обращается в нуль, приходим к уравнению для определения второй искомой функции 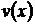
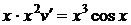 ,
, 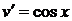 ,
,
общее решение которого и есть вторая искомая функция
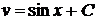 .
.
Следовательно, общее решение данного уравнения
 .
.
42. 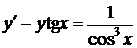 ,
, 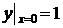 .
.
Применим метод Эйлера, поскольку очевиден для данного уравнения интегрирующий множитель ((50) условие 1)
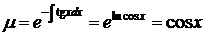 .
.
Умножая обе части данного уравнения на 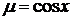 , получим
, получим
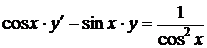 .
.
Так как в левой части производная произведения, квадратурой вычисляем общий интеграл уравнения
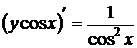 ,
, 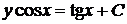 .
.
Используя начальные условия, из общего интеграла получаем для нахождения константы С уравнение
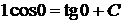 , откуда
, откуда 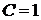 ;
;
следовательно, решение поставленной задачи Коши
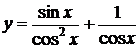 ,
, 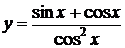 .
.
43. 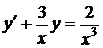 ,
, 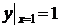 .
.
Согласно методу вариации постоянной, рассмотрим соответствующее однородное уравнение
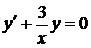 , или
, или 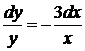 ,
,
квадратурой находим его общее решение
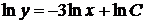 ,
, 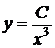 .
.
Далее ищем решение неоднородного уравнения в виде
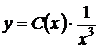 .
.
Подставляя это выражение в данное уравнение, находим 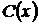
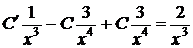 ,
, 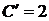 ,
, 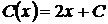 .
.
Следовательно, общее решение данного уравнения есть
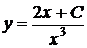 .
.
Из общего решения, используя начальные условия, определяем постоянную интегрирования 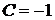 и получаем решение поставленной задачи Коши
и получаем решение поставленной задачи Коши
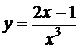 .
.
44. 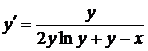 . Это нелинейное уравнение, однако, линейным является перевернутое уравнение, если рассматривать х как функцию от у
. Это нелинейное уравнение, однако, линейным является перевернутое уравнение, если рассматривать х как функцию от у
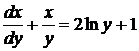 .
.
В соответствии с методом вариации произвольной постоянной, решаем соответствующее однородное уравнение
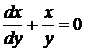 ,
, 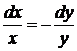 ,
, 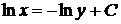 ,
, 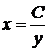 .
.
Будем искать решение перевернутого уравнения в виде
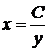 ,
,
где 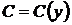 – неизвестная функция от у. Подставляем это выражение в неоднородное (перевернутое) уравнение
– неизвестная функция от у. Подставляем это выражение в неоднородное (перевернутое) уравнение
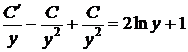 ,
, 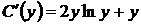 .
.
Отсюда, интегрируя по частям первое слагаемое, имеем
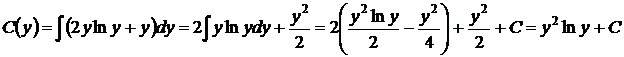 .
.
Подставляя найденное выражение для неизвестной функции С в искомый вид решения, получаем общее решение перевернутого уравнения, а, значит, общий интеграл данного уравнения
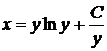 .
.
45. 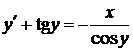 . Это нелинейное уравнение, умножая обе его части на
. Это нелинейное уравнение, умножая обе его части на 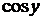 и делая замену
и делая замену 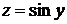 , приводим данное уравнение к линейному относительно новой неизвестной функции
, приводим данное уравнение к линейному относительно новой неизвестной функции 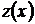
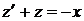 .
.
Следуя методу Лагранжа, сначала находим общее решение соответствующего однородного уравнения
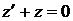 ,
, 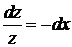 ,
, 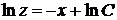 ,
, 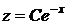 ,
,
а затем, варьируя постоянную интегрирования С, находим общее решение (интегрированием по частям) неоднородного промежуточного уравнения
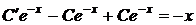 ,
, 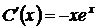 ;
;
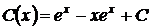 ;
; 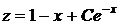 .
.
Возвращаясь к старым переменным, запишем общий интеграл данного уравнения
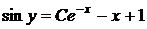 .
.
Уравнение Бернулли
Дифференциальное уравнение Бернулли имеет вид
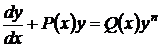 , (64)
, (64)
где заданные функции 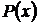 и
и 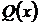 определены и непрерывны в интервале
определены и непрерывны в интервале 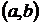 , а n – вещественное число, отличное от 0 и 1 (так как при
, а n – вещественное число, отличное от 0 и 1 (так как при 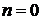 или
или 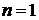 уравнение Бернулли обращается в линейное дифференциальное уравнение).
уравнение Бернулли обращается в линейное дифференциальное уравнение).
Уравнение Бернулли (64) приводится к линейному введением новой переменной
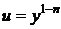 ,
, 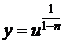 . (65)
. (65)
Для новой искомой функции и получаем уравнение
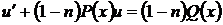 . (66)
. (66)
Согласно формуле (59), общее решение уравнения (66)
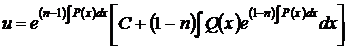 , (67)
, (67)
следовательно, общее решение уравнения Бернулли
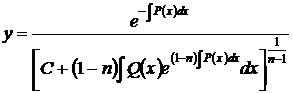 . (68)
. (68)
Из уравнения (64) видно, что при 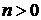 существует решение
существует решение 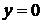 этого уравнения.
этого уравнения.
Если 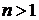 , то прямая
, то прямая 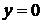 является асимптотой всех интегральных кривых уравнения Бернулли, а, значит, частным решением этого уравнения, которое получается из формулы (68) при
является асимптотой всех интегральных кривых уравнения Бернулли, а, значит, частным решением этого уравнения, которое получается из формулы (68) при 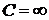 . (В формуле (68) можно положить
. (В формуле (68) можно положить 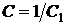 и, заново переписав формулу, получить решение
и, заново переписав формулу, получить решение 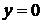 при
при 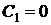 ).
).
Если 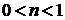 , то
, то 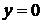 является особым решением уравнения Бернулли, оно не может быть получено из общего решения (68) ни при каком значении постоянной интегрирования С.
является особым решением уравнения Бернулли, оно не может быть получено из общего решения (68) ни при каком значении постоянной интегрирования С.
Из вышеизложенного следует, что вопросы, связанные с интегрированием и изучением поведения решений уравнения Бернулли, сводятся к аналогичным вопросам для линейного уравнения. Однако, классически уравнение (64) интегрируется непосредственно применением мультипликативной подстановки Бернулли (55) (или методом Лагранжа) без предварительного сведения его к линейному.
Примеры.
46.
