Дифференциальные уравнения: учебное пособие.-СПб:СПГУВК, 2011 - 34 с.

ФЕДЕРАЛЬНОЕ АГЕНТСТВО МОРСКОГО И РЕЧНОГО

ТРАНСПОРТА

ФЕДЕРАЛЬНОЕ БЮДЖЕТНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

УНИВЕРСИТЕТ ВОДНЫХ КОММУНИКАЦИЙ»

———————————————————————————————

М.Ю. Ястребов

МАТЕМАТИКА

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Санкт-Петербург

УДК

ББК

Рецензенты:

К. ф.-м.н., доцент

Кузнецов В.О.,

К. ф.-м.н., доцент

Гулевич Н.М.

Ястребов М.Ю.

Дифференциальные уравнения: учебное пособие.-СПб:СПГУВК, 2011 - 34 с.

Предназначено для студентов технических и информационных специальностей.

Содержание соответствует рабочей программе дисциплины «Математика».

Печатается по решению редакционно-издательского совета Санкт-Петербургского государственного университета водных коммуникаций.

УДК

ББК

©Санкт-Петербургский государственный

университет водных коммуникаций, 2012

ИСХОДНЫЕ ПОНЯТИЯ

Определение. Обыкновенным дифференциальным уравнением называется уравнение вида

, (1)

связывающее независимую переменную 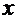, неизвестную функцию и ее производные различных порядков.

Функция предполагается заданной на некотором промежутке (который также, как правило, не задан изначально и подлежит определению вместе с ).

Замечание. В отличие от дифференциальных уравнений вида (1), в которых искомая функция зависит только от одной переменной, уравнения, связывающие неизвестную функцию нескольких независимых переменных и ее частные производные различных порядков, называются уравнениями в частных производных, или уравнениями математической физики.

Например, уравнение теплопроводности описывает изменение температуры тела в каждой его точке в зависимости от времени :

.

В дальнейшем, говоря о дифференциальных уравнениях, мы будем иметь ввиду обыкновенные дифференциальные уравнения.

Определение. Порядком дифференциального уравнения называется порядок старшей производной, входящей в уравнение.

Таким образом уравнение (1) задает дифференциальное уравнение 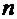-го порядка.

Напомним, что под промежутком понимается любой из возможных промежутков, содержащий или не содержащий граничные точки: .

Определение. Решением дифференциального уравнения (1) на промежутке называется функция , дифференцируемая 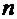раз и обращающая его на в тождество (то есть в равенство, верное при всех ).

Примеры.

(а) — уравнение 1-го порядка;

(б) — уравнение 2-го порядка;

(в) — уравнение 4-го порядка.

Нетрудно проверить (проделайте это самостоятельно), что для уравнения (а) решениями на , являются, в частности, функции . Для уравнения (б) решениями при всех вещественных 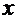являются функции и . Для уравнения (в) всякая функция вида , где — произвольная постоянная, является решением на .

Определение. График решения 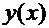дифференциального уравнения называется интегральной кривой.

Процесс отыскания решения дифференциального уравнения называют интегрированием данного уравнения.

МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ

Определение. Уравнением с разделенными переменными называетсядифференциальное уравнение первого порядка вида

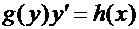, (4)

с непрерывными функциям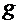и и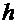

Смысл этого термина заключается в том, что переменные 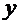и 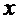разделены по разным частям равенства (4).

Напомним, что, согласно определению, дифференциал функции 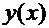есть произведение производной на дифференциал независимой переменной: 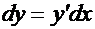. Если умножить обе части равенства (4) на 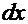, получим:

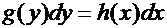. (5)

Это другой, более традиционный способ записи уравнения с разделенными переменными.

Теорема. Если в уравнении (5) функци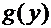и и 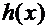имеют первообразные 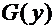и 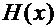, то общий интеграл уравнения имеет вид:

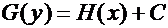, (6)

где 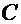— произвольная постоянная.

Замечание. Если для обозначения первообразных использовать символ неопределенного интеграла, то общий интеграл записывается в виде:

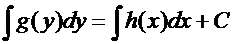. (7)

Доказательство. Опуская доказательство того, что уравнение (6) действительно задает неявную функцию 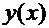, убедимся, что 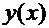удовлетворяет уравнению (4). Для этого продифференцируем по 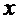равенство (6), применяя для левой части правило производной сложной функции с промежуточной переменной :

,

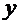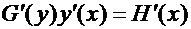или, учитывая, что 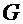и 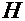первообразные для 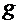и :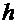

.

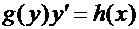Остается убедиться, что за счет выбора значения произвольной постоянной 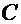можно обеспечить выполнение любых начальных условий 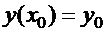. Подставляя начальные условия в (6), получаем:

. ▄

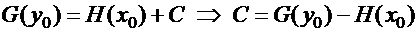Примеры. 1. Для уравнения 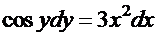найдем общий интеграл и частный интеграл для начальных условий 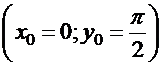. Имеем:

—

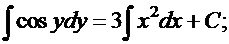
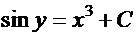это общий интеграл.

Подставим теперь в общий интеграл начальные условия и найдем соответствующее значение константы :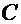

.

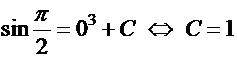Следовательно, частный интеграл, дающий решение задачи Коши, имеет вид:

.

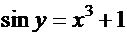2. Рассмотрим уравнение 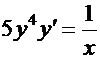с начальными условиями 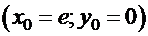. Умножая обе части уравнения на 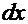и затем интегрируя, получаем:

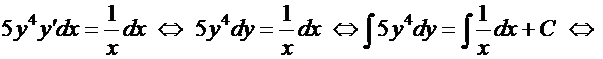
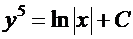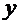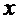– это общий интеграл. Выражая отсюда явно через и 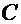, получаем общее решение: 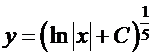. Подстановка начальных условий в общее решение дает: 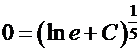, так что 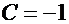. Следовательно, функция 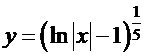является решением задачи Коши.

Определение. Уравнением с разделяющимися переменными называетсядифференциальное уравнение первого порядка вида

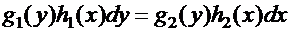, (8)

с непрерывными функциями .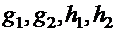

В этом уравнении каждая из частей является произведением двух множителей, один из которых зависит только от 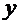, а другой – только от .

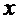От этого уравнения легко перейти к уравнению с разделенными переменными, деля обе части на произведение 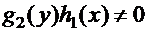(«разделяя переменные»):

.

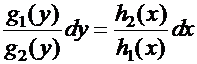Примеры. 1. 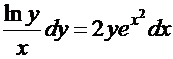. Обе части разделим на 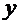и умножим на 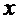: 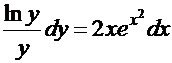. Интегрируем:

—

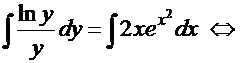
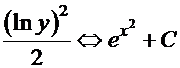общий интеграл.

2. 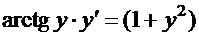; начальные условия: 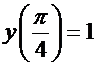. Записываем производную 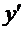как отношение дифференциалов:

.

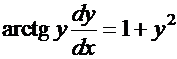Обе части умножим на 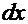, разделим на 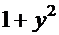и проинтегрируем:

—

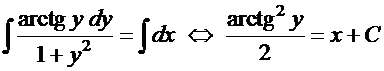общий интеграл. Найдем теперь частный интеграл, удовлетворяющий начальным условиям. Подставляя начальные условия в полученное уравнение, имеем:

; .

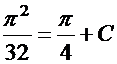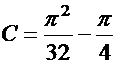Следовательно, частный интеграл, дающий решение задачи Коши, имеет вид:

.

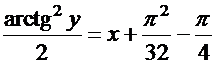Основные понятия

Определение. Линейным уравнением второго порядка называется уравнение вида:

(14)

с непрерывными на интервале функциями и .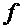

Из теоремы 2, приведенной на с. 6, следует, что указанная непрерывность гарантирует при существование и единственность решения задачи Коши с любыми начальными данными .

Определение. Однородным линейным уравнением второго порядка называется уравнение с нулевой правой частью:

. (15)

ЛИТЕРАТУРА

1. Пискунов Н.С. Дифференциальное и интегральное исчисления, т. 1-2.- Интеграл-Пресс, 2005. – 416 с.

2. Данко П.Е. и др. Высшая математика в упражнениях и задачах,

часть 1,2. М.: "Оникс 21 век". – 2003.

3. Волков Н.И., Голоскоков П.Г., Шкадова А.Р. Матрицы, опреде-

лители и системы линейных уравнений. Учебное пособие. – СПб.:

СПбГУВК. – 2006.

4. Ястребов М.Ю. Производная и исследование функций. СПб.: СПГУВК, 2003. – 45 с.

5. Ястребов М.Ю. Неопределенный и определенный интегралы. СПб.: СПГУВК, 2004. – 55 с.

6. Ястребов М.Ю. Функции нескольких переменных. СПб.: СПГУВК, 2006. – 48 с.

7. Лащенов В.К. Комплексные числа. СПб.: СПГУВК, 2010. – 8 с.

СОДЕРЖАНИЕ

	Исходные понятия…………………………………………..
	Начальные условия и задача Коши………………………...
	Общее решение и общий интеграл………………………...
	Метод разделения переменных…………………………….
	Однородное уравнение первого порядка………………….
	Линейное уравнение первого порядка…………………….
	Уравнения, допускающие понижение порядка…………...
7.1	Уравнение вида ………………………………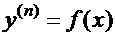
7.2	Уравнение, не содержащее явно неизвестную функцию …………………………………………………..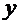
7.3	Уравнение, не содержащее явно независимую переменную ………………………………………………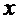
	Линейное уравнение второго порядка……………………..
8.1	Основные понятия…………………………………………..
8.2	Свойства решений однородного линейного уравнения…..
8.3	Линейное уравнение с постоянными коэффициентами…..
8.4	Структура общего решения неоднородного линейного Уравнения……………………………………………………
	Метод вариации произвольных постоянных (метод Лагранжа)……………………………………………
	Метод неопределенных коэффициентов…………………..
	Литература…………………………………………………..

Михаил Юрьевич Ястребов

МАТЕМАТИКА

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Учебное пособие

ФЕДЕРАЛЬНОЕ АГЕНТСТВО МОРСКОГО И РЕЧНОГО

ТРАНСПОРТА

ФЕДЕРАЛЬНОЕ БЮДЖЕТНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

УНИВЕРСИТЕТ ВОДНЫХ КОММУНИКАЦИЙ»

———————————————————————————————

М.Ю. Ястребов

МАТЕМАТИКА

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Санкт-Петербург

УДК

ББК

Рецензенты:

К. ф.-м.н., доцент

Кузнецов В.О.,

К. ф.-м.н., доцент

Гулевич Н.М.

Ястребов М.Ю.

Дифференциальные уравнения: учебное пособие.-СПб:СПГУВК, 2011 - 34 с.

Предназначено для студентов технических и информационных специальностей.

Содержание соответствует рабочей программе дисциплины «Математика».

Печатается по решению редакционно-издательского совета Санкт-Петербургского государственного университета водных коммуникаций.

УДК

ББК

©Санкт-Петербургский государственный

университет водных коммуникаций, 2012

ИСХОДНЫЕ ПОНЯТИЯ

Определение. Обыкновенным дифференциальным уравнением называется уравнение вида

, (1)

связывающее независимую переменную 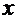, неизвестную функцию и ее производные различных порядков.

Функция предполагается заданной на некотором промежутке (который также, как правило, не задан изначально и подлежит определению вместе с ).

Замечание. В отличие от дифференциальных уравнений вида (1), в которых искомая функция зависит только от одной переменной, уравнения, связывающие неизвестную функцию нескольких независимых переменных и ее частные производные различных порядков, называются уравнениями в частных производных, или уравнениями математической физики.

Например, уравнение теплопроводности описывает изменение температуры тела в каждой его точке в зависимости от времени :

.

В дальнейшем, говоря о дифференциальных уравнениях, мы будем иметь ввиду обыкновенные дифференциальные уравнения.

Определение. Порядком дифференциального уравнения называется порядок старшей производной, входящей в уравнение.

Таким образом уравнение (1) задает дифференциальное уравнение 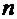-го порядка.

Напомним, что под промежутком понимается любой из возможных промежутков, содержащий или не содержащий граничные точки: .

Определение. Решением дифференциального уравнения (1) на промежутке называется функция , дифференцируемая 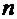раз и обращающая его на в тождество (то есть в равенство, верное при всех ).

Примеры.

(а) — уравнение 1-го порядка;

(б) — уравнение 2-го порядка;

(в) — уравнение 4-го порядка.

Нетрудно проверить (проделайте это самостоятельно), что для уравнения (а) решениями на , являются, в частности, функции . Для уравнения (б) решениями при всех вещественных 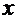являются функции и . Для уравнения (в) всякая функция вида , где — произвольная постоянная, является решением на .

Определение. График решения 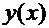дифференциального уравнения называется интегральной кривой.

Процесс отыскания решения дифференциального уравнения называют интегрированием данного уравнения.