ГЛАВА 3: Линейные системы дифференциальных уравнений с постоянными коэффициентами.

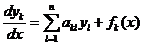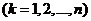, (1), где 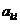- постоянные вещественные числа, 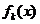- непрерывны в интервале (a,b).

Так как общее решение неоднородной системы связано с построением общего решения соответствующей однородной системы, то, естественно, сначала рассмотрим однородную систему 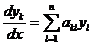, 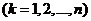(2).

Фундаментальная система решений, из ранее доказанного, существует в интервале .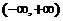

Для системы (2) всегда можно построить ФСР из элементарных целых функций.

Решение системы (2) будем искать в виде 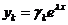, 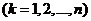(3).

Подставляя (3) в (2), получаем , .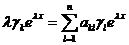

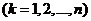Сокращая на 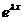, имеем линейную однородную систему относительно , .

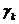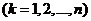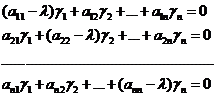(4).

Нетривиальное решение система (4) имеет, когда определитель её равен нулю, т.е. 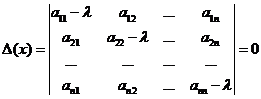(5).

Уравнение (5) называется характеристическим уравнением системы (2), а корни его называются характеристическими числами. 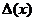представляет собой многочлен степени n относительно λ.

Случай 1. Все корни характеристического многочлена 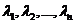- действительные и различные, т.е. .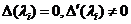

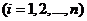Покажем, что в этом случае ранг матрицы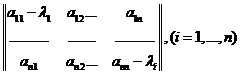

равен n-1.

Рассмотрим:

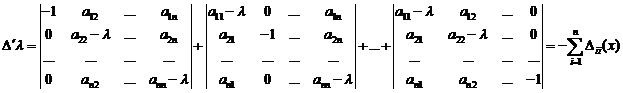
где 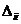- алгебраические дополнения элемента 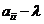определителя .

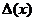Следовательно, хоть один из определителей (n-1)-го порядка отличен от нуля.

Система (4) имеет ненулевое решение, которое определяется с точностью до множителя. Таким образом, получим n решений системы (2).

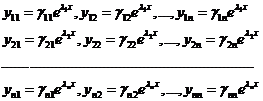(6) - ФСР системы (2).

Поэтому, в силу основной теоремы, общее решение системы (2) в области 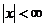, 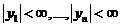имеет вид:

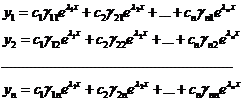(7).

Пример.

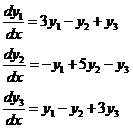(8).

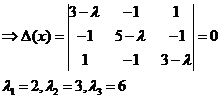
Подставляя 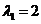в систему (4), получаем:

.

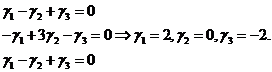
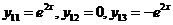Аналогично находим при :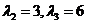

.

.

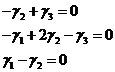
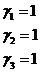
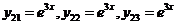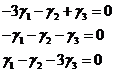
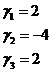
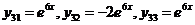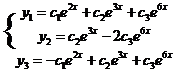(9) – общее решение системы (8).

Случай 2. Все корни различны, но среди них имеются комплексные.

a + ib u a – ib - простые корни характеристического уравнения. Корню a + ib, согласно формуле (3), соответствует решение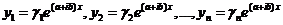

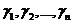- комплексные числа. Поэтому y₁,..., y_n – комплексное решение.

Отделяя в нём вещественную и мнимую части, получим два вещественных решения. Сопряжённый корень a – ib не порождает новых вещественных решений.

Итак, паре комплексно сопряжённых корней соответствует два вещественных линейно независимых решения.

Пример. 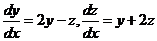(10)

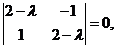
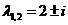
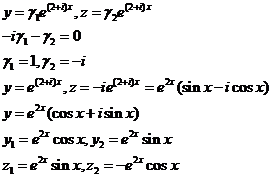
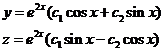(11) – общее решение данной системы.

Случай 3. Среди корней характеристического уравнения имеются кратные корни.

Как построить в этом случае ФСР для системы (2) даёт ответ следующая теорема.

Теорема.

Если 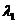есть характеристическое число кратности k, то ему соответствует решение вида 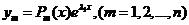, где P₁(x), P₂(x),..., P_n(x) – полиномы от х степени, не превышающей k-1, имеющие в совокупности k произвольных коэффициентов. Полиномы могут вырождаться в постоянные числа. В таком случае k-кратному характеристическому числу 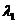будет соответствовать решение вида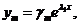 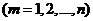. Но среди коэффициентов 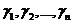k коэффициентов являются произвольными.

Пример.

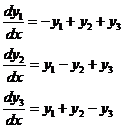(12)

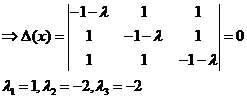
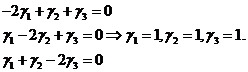
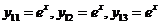
λ=-2 - корень кратности два, ему соответствуют решения

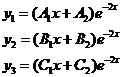(13). Сокращая их на 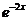и подставляя 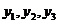в систему (12), получаем:

(14).

Сравнивая в системе (14) коэффициенты при одинаковых степенях, получаем следующие соотношения:

.

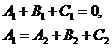
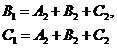
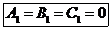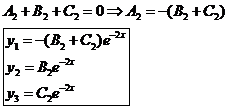
Положим : .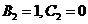

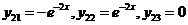Положим : .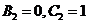

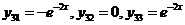Таким образом, 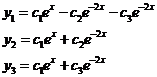(15).

(15) – общее решение системы (12).

ЛЕКЦИЯ 10:

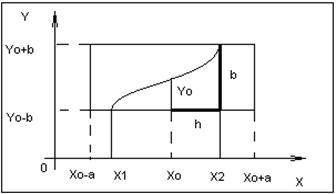
27. Теорема Пикара:

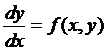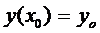Если в уравнении , при (1)

1. 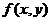определена и непрерывна в области 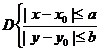и, следовательно, ограничена в области 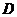, т.е. .

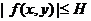2. Удовлетворяет в области 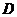условию Липшица по :

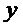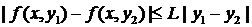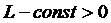, (2)

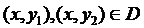, то существует единственное решение 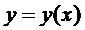, удовлетворяющее условию 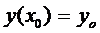, а в промежутк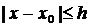е , где 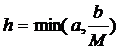и решение это определено и непрерывно дифференцируемо для 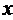из отрезка 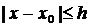и не выходит за пределы области 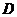при этих значениях .

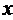Поясним некоторые условия теоремы

Пикара.

1.

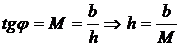
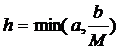
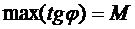
2. На практике условие Липшица заменяется 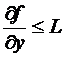. Из этого условия следует условие Липшица.

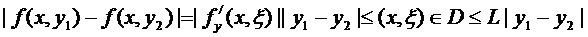
Обратно, из условия Липшица не следует условие .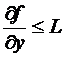

Примером может служить функция 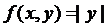. Производная не принадлежит в .

Доказательство:

Предположим, что существует решение 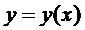с условием 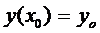. Тогда 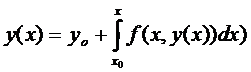(3)

Уравнение (1) и (3) равносильны. Решение (1) является решением (3).

Если найдено решение интегрального уравнения (3), тем самым найдено решение уравнения (1).

Доказывать существование и единственность решения уравнения (1) при заданных условиях будем методом приближений.

За нулевые приближения возьмём ,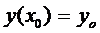

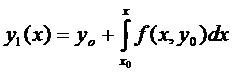
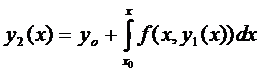(4)

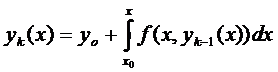
1. Покажем, что все члены функциональной последовательности (4) определены и непрерывны на отрезке 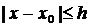и не выходят за пределы области .

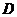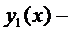определена и непрерывна,

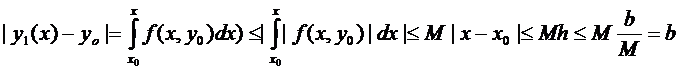Предположим, что 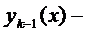определена и непрерывна на промежутках , .

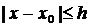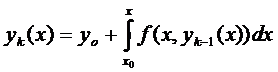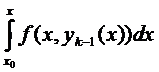даже дифференцируемая функция (интеграл с верхним переменным пределом).

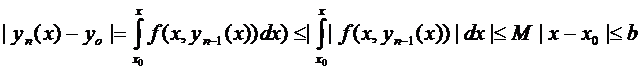
Таким образом, все члены последовательности (4) определены и непрерывны в промежутках 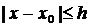и не выходят при этих значениях за пределы области .

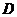2. Докажем равномерную сходимость функциональной последовательности (4) в промежутке .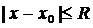

Вместо (4) будем рассматривать функциональный ряд:

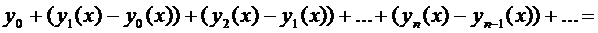
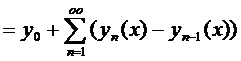(5)

Сходимость последовательности (4) равносильна сходимости ряда (5), так как частные суммы ряда (5) являются .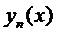

Оценим разность 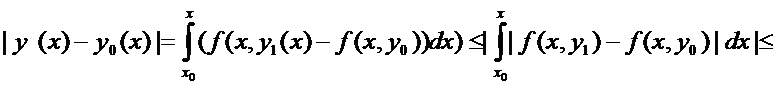{применяем условие Липшица} ,

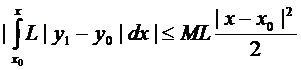Учитывая .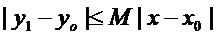

Аналогично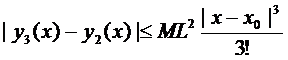

И так далее.

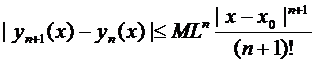(6)

Предполагая, что это утверждение верно для 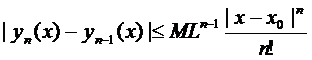доказывается (6).

Члены ряда для всех значений 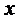из промежутка 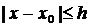не превосходят по абсолютной величине соответствующих членов следующего ряда с положительными членами:

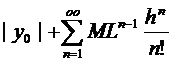(7)

Ряд (7) сходится. Сумма этого ряда равна 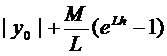(8)

Согласно признаку Ваейрштрасса ряд (5) сходится равномерно в промежутке .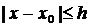

Пусть 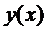сумма ряда (5) или предельная функция последовательности (4).

Тогда по теореме непрерывности суммы равномерно сходящегося ряда функция 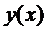также непрерывна в промежутке .

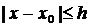1. Покажем, что функция 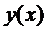является решение интегрального уравнения (3) и её значения не выходят за пределы област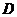и при .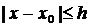

Так как 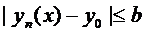, то переходя к пределу при 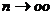получим:

.

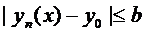В формуле (4) перейдём к пределу при :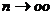

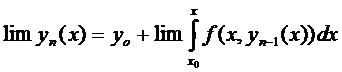
Докажем, что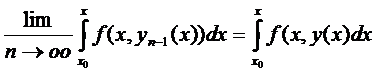

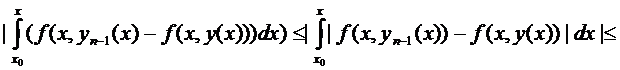
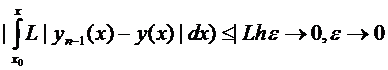
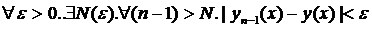
для 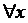из промежутка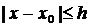

Итак,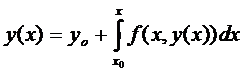

1. Докажем, что получено решение единственное.

Предположим, что существует ещё одно решение 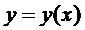, удовлетворяющее тем же начальным условиям, которое определено и непрерывно в промежутке 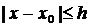и не выходит при этих значениях 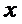за пределы области .

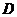Итак,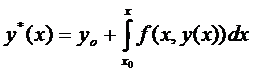

Оценим

,

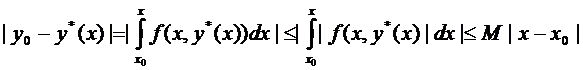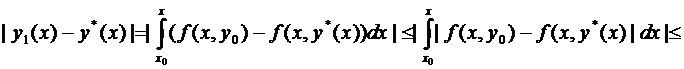
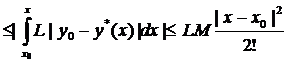и т.д.

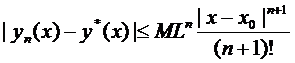(9)

Устремляем 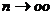в формуле (9):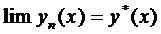

Откуда .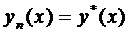

Замечание:

1. Формула (9) даёт оценку погрешности нашего приближения к решению .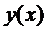

2. Формула (8) даёт оценку решения .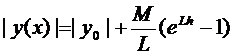

3. За нулевое приближение не обязательно брать 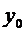. Можно брать любую непрерывно дифференцируемую функцию, значения которой не выходят за пределы области .

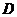Пример:

, ,

.

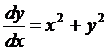
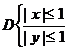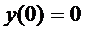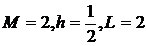
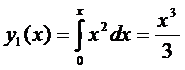
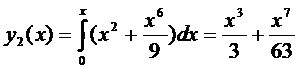
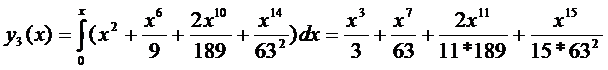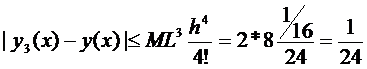
ЛЕКЦИЯ 11: