Нахождение частного решения неоднородного уравнения методом неопределённых коэффициентов.
1.
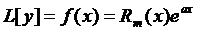 (14), где Rm(x) полином степени m с вещественными или комплексными коэффициентами, а – постоянное вещественное или комплексное или равное нулю число.
(14), где Rm(x) полином степени m с вещественными или комплексными коэффициентами, а – постоянное вещественное или комплексное или равное нулю число.
Случай 1.1:
P(a)≠0
В этом случае частное решение y1 уравнения L[y] = 0 (1) следует искать в виде:
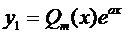 , где
, где 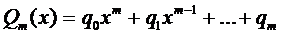 (15)
(15)
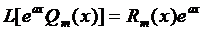 ,
,
где 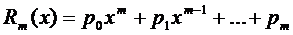 (16)
(16)
Распишем левую часть (16), используя свойства оператора L подробнее
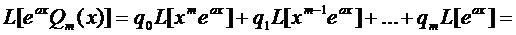
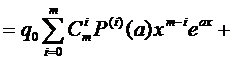
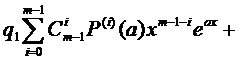
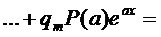
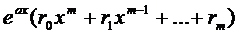 (17)
(17)
Сокращая на 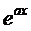 и сравнивая коэффициенты при одинаковых степенях
и сравнивая коэффициенты при одинаковых степенях 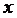 , получаем:
, получаем:
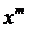 :
: 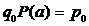
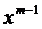 :
: 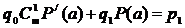
… (18)
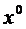 :
: 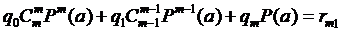
Так как P(a) ≠ 0, все qi находятся из (18) последовательно единственным образом.
Случай 1.2:
«а» является корнем характеристического многочлена кратности k, т.е. P (a) = 0, P/ (a) = 0, …, P( k-1) (a) = 0, P( k) (a) ≠ 0.
Тогда частное решение ищется в виде 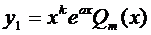 (19)
(19)
Доказательство аналогично случаю 1.
2.
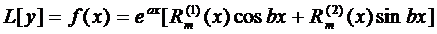 (20)
(20)
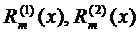 - заданные полиномы от
- заданные полиномы от 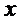 степени равной или меньшей m, причём хоть один из них имеет степень m.
степени равной или меньшей m, причём хоть один из них имеет степень m.
Заменяя 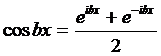 ,
, 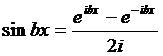 (21)
(21)
2. сводится к случаю 1.
Используем результаты случая 1.
Случай 2.1:
Число 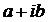 не является корнем характеристического уравнения. Тогда частное решение имеет вид:
не является корнем характеристического уравнения. Тогда частное решение имеет вид:
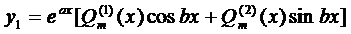 (22)
(22)
где 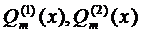 –полиномы степени m с неопределёнными коэффициентами, которые определяются единственным образом.
–полиномы степени m с неопределёнными коэффициентами, которые определяются единственным образом.
Случай 2.2:
Число 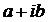 является корнем характеристического уравнения кратности k (k≥1). Тогда частное решение имеет вид:
является корнем характеристического уравнения кратности k (k≥1). Тогда частное решение имеет вид:
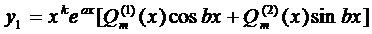 (23)
(23)
где 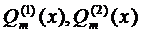 –полиномы степени m с неопределёнными коэффициентами, которые определяются единственным образом.
–полиномы степени m с неопределёнными коэффициентами, которые определяются единственным образом.
Пример 1:
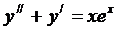 ,
,
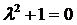 – характеристическое уравнение,
– характеристическое уравнение,
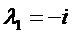
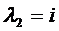
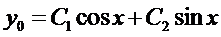 – общее решение однородного уравнения.
– общее решение однородного уравнения.
Случай ?.?:
а =1 не является корнем характеристического уравнения. Тогда частное решение имеет вид:
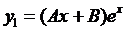 ,
, 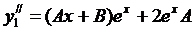
Подставляя значения 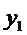 и
и 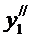 в уравнение и сокращая на e x , получаем:
в уравнение и сокращая на e x , получаем: 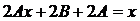 .
.
Откуда 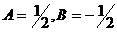 .
. 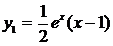 .
.
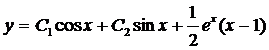 –общее решение данного уравнения.
–общее решение данного уравнения.
Пример :
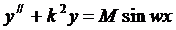 ,
,
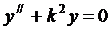 ,
,
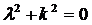 ,
,
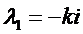
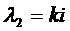
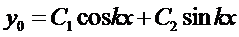 – общее решение однородного уравнения.
– общее решение однородного уравнения.
1) 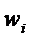 не является корнем характеристического уравнения.
не является корнем характеристического уравнения.
Тогда 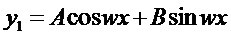

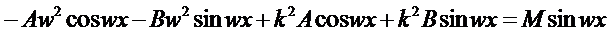
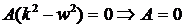
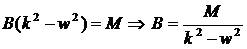
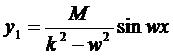
2) 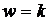 ,
, 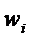 является корнем характеристического уравнения.
является корнем характеристического уравнения.
Тогда 
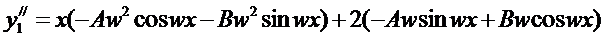 Подставляя значения
Подставляя значения 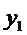 и
и 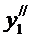 в уравнение , получаем:
в уравнение , получаем:
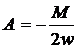 ,
, 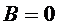
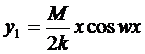 , такой член называется вековым.
, такой член называется вековым.
ЛЕКЦИЯ 5:
Приведение однородного линейного уравнения n-го порядка к уравнению с постоянными коэффициентами при помощи замены независимой переменной.
Рассмотрим линейное однородное уравнение 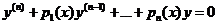 (1).
(1).
Сделаем замену независимой переменной 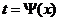 :
:
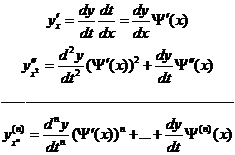 (2)
(2)
Подставим (2) в (1) и разделим на 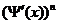 , получим :
, получим : 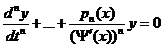 (3).
(3).
Необходимо, чтобы 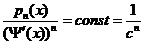 (4), следовательно:
(4), следовательно:
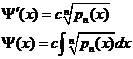 (5).
(5).
Пример. Уравнение Чебышева.
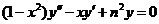
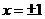 - особые точки уравнения ,
- особые точки уравнения , 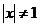 .
.
Построим общее решение уравнения Чебышев при 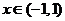
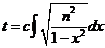 (7). Возьмём
(7). Возьмём 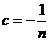 , тогда
, тогда 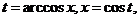
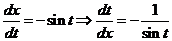 ;
;  (8)
(8)
Подставляя (8) в уравнение Чебышева (6), получаем:
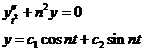
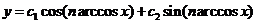 (9) – общее решение уравнения (6)
(9) – общее решение уравнения (6)
Линейное уравнение Эйлера.
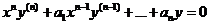 (1)
(1)
х=0 – особая точка уравнения (1)
Решение этого уравнения существует и единственно при 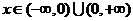 .
.
Будем рассматривать уравнение (1) при 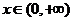 .
.
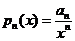 . Поэтому, согласно №14 :
. Поэтому, согласно №14 : 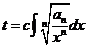 (2) ,
(2) , 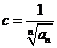 .
.
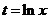 или
или 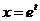 (3).
(3).
Тогда
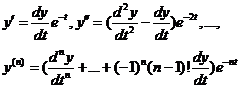 (4).
(4).
Подставляя (4) в уравнение (1), получаем однородное линейное уравнение n-го порядка с постоянными коэффициентами. Найдя общее решение и полагая в нём 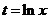 , мы получим общее решение уравнения Эйлера.
, мы получим общее решение уравнения Эйлера.
Пример 1. 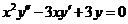 .
.
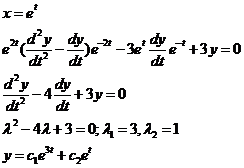
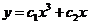 - общее решение однородного уравнения Эйлера.
- общее решение однородного уравнения Эйлера.
Пример 2. 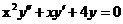
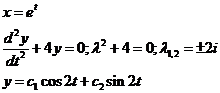
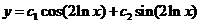 - общее решение уравнения Эйлера.
- общее решение уравнения Эйлера.
