Несистематические БПФ-укорочения

Порядок мультипликативной группы поля 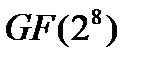является составным числом n=255=3*5*17. Группа 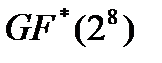является циклической и порождается примитивным элементом α; она содержит 255 элементов: 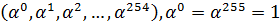. Эта группа имеет циклические подгруппы порядка 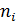( 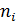делят ).

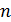В таблице 1 приведены циклические подгруппы мультипликативной группы поля .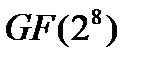

Таблица 1.

Циклические подгруппы мультипликативной группы поля

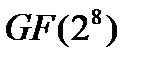
Порядок подгруппы	Порождающий элемент	Подгруппа

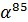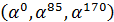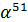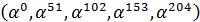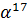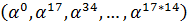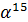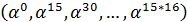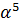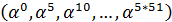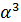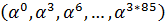В основе несистематического кодированияукороченных РС-кодов лежит дискретное преобразование Фурье (ДПФ) на группе, образуемой ненулевыми элементами поля.

Кодовое слово 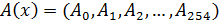задается как ДПФ информационного вектора 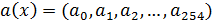c 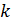информационными символами и 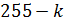нулями, где 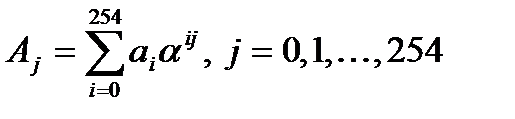, а в качестве примитивного элемента 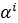выбран корень неприводимого многочлена .

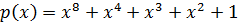Aлгоритм трехмерного ДПФ позволяет вычислить элементы 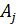кодового вектора по формуле:

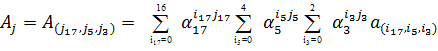(24)

Рассмотрим преобразование Фурье длины 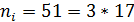в поле 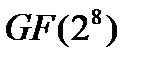. Элементами этого преобразование 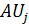должны быть элементы подгруппы, образованной примитивным элементом 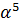(в соответствии с таблицей 1). Перекодируем укороченный вектор 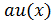(вектор длины 51) в полный вектор 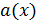(длины 255) таким образом, чтобы все координаты 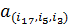, для которых 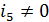, были нулевыми. Практически это означает, что мы разместим укороченный вектор 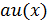только в одной плоскости БПФ-куба там, где 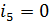. Тогда формулу (24) можно переписать в виде:

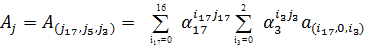(25)

А это означает переход к ДПФ с ядром 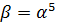для вектора 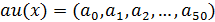. Преобразование Фурье вычисляется как значение многочлена 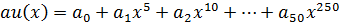в точках поля: 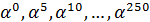, что эквивалентно работе в подгруппе с ядром : .

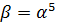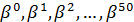Очевидно, что для реализации БПФ-укорочения длины 85 с порождающим элементом 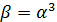из формулы (24) необходимо исключить суммирование по 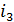, что достигается путем размещения укороченного вектора в плоскости БПФ-куба там, где 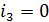. Это означает переход к ДПФ с ядром 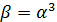для мультипликативной подгруппы порядка 85 с шагом 3.

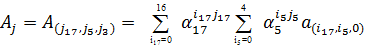(26)

Проводя аналогичные рассуждения можно построить формулы вычисления ДПФ для всех циклических подгрупп, указанных в таблице 1.Эти БПФ-укорочения можно применить для кодирования укороченными кодами Рида-Соломона над полем 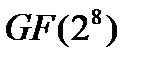длин n=85,51,17,15,5,3.

ЗАКЛЮЧЕНИЕ

На основании китайской теоремы об остатках получен результат, существенно понижающий вычислительную сложность ДПФ. Приведены формулы для трехмерного преобразования Фурье поле 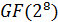. Построены алгоритмы быстрого преобразование Фурье (БПФ) длин 3, 5 и 17 на основе алгоритма Рейдера и алгоритма Винограда вычисления циклической свертки. Показана эквивалентность между вычислением ДПФ простой длины и вычислением циклической свертки.

На основании трехмерного преобразования Фурье построеныукороченные преобразования длин 15, 51, 85, которые рационально применять, когда не требуется кодировать слова длины 255. Показана эквивалентность между укорочением преобразования и переходом на соответствующую ему подгруппу мультипликативной группы поля.

В приложении представлен программный комплекс, реализующий построение поля 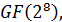основные операции в этом поле, вычисление значения произвольного многочлена в любой точке поле, вычисление ДПФ, ОДПФ, трехмерного преобразования Фурье и БПФ длин 255,85,51,15,17,5,3, кодирование кодом Рида-Соломона в частотной области.

Проведенные вычислительные эксперименты показали практическую эффективность перехода от ДПФ к трехмерному преобразованию: если на вычисление ДПФ длины 255 затрачивается примерно 300-350 мс машинного времени, то трехмерное преобразование занимает от 20 до 35 мс. При этом на вычисление БПФ длины 255 затрачивается всего 13-17 мс.

Разработанный программный комплекс можно применять при создании систем хранения и передачи данных с повышенной надежностью. Удобный и наглядный пользовательский интерфейс интуитивно понятен и не вызовет проблем у разработчиков этих систем.

Языком реализации выбранBorlandDelphiEnterprise 2007.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1. Берлекэмп Э. Р. Алгебраическая теория кодирования. М.: Мир, 1971

2. Nussbaumer H. J. Fast Fourier Transform and Convolution Algorithms. – Springer-Verlag: Berlin, Heidelberg, New York, 1981.

3. Помехоустойчивое кодирование и надежность ЭВМ. М.: Наука, 1987.

4. Макмеллан Дж. Х., Рейдер Ч. М. Применение теории чисел в цифровой обработке сигналов. М.: Радио и связь, 1983.

5. Блейхут Р. Теория и практика кодов, контролирующих ошибки. М.: Мир, 1986.

6. Зюко А.Г., Кловский Д.Д., Назаров М.В., Финк Л.М. Теория передачи сигналов. М: Радио и связь, 2001 г.

7. Золотарев В. В. Помехоустойчивое кодирование. Методы и алгоритмы:

справочник / В. В. Золотарев, Г. В. Овечкин. – М.: Горячая линия –

Телеком, 2004. – 126 с.

8. Блейхут Р. Быстрые алгоритмы цифровой обработки сигналов. М.: Мир, 1989.

9. Лидл Р., Нидеррайтер Г. Конечные поля, т.1. М.: Мир, 1988

10. Волошина В. Н., Руднева И. В. Надежное хранение информации с помощью кодов Рида-Соломона: Препр. Владивосток: ИАПУ ДВНЦ АН СССР, 1987, 13 с.

11. Волошина В. Н., Герасимов В. В., Руднева И. В., Программно-технологическая система хранения информации с повышенной надежностью: Препр. Владивосток: ИАПУ ДВО АН СССР, 1989, 22 с.

ПРИЛОЖЕНИЯ

Приложение 1.