Мультипликативный порядок элементов поля. Примитивные элементы. Другой подход к построению расширения поля Галуа

В любом поле 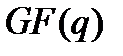, является ли оно простым или расширенным, определена операция 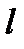–кратного умножения элемента 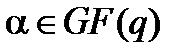. Естественно назвать такое произведение 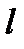–ой степенью элемента 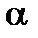, обозначив его как

.

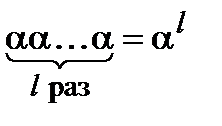Тогда

,

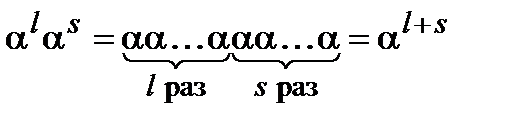и для любого ненулевого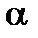

.

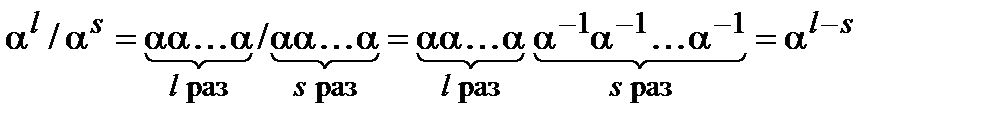Следовательно, в конечных полях действуют те же самые правила обращения с целочисленными степенями элементов, что и в обычной арифметике.

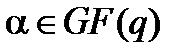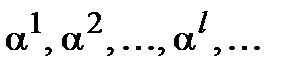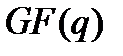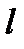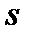
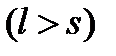Возьмем некоторый ненулевой элемент и рассмотрим его степени вида . Поскольку все они являются элементами поля , то вследствие его конечности лишь ограниченное число подобных степеней будет различными, т.е. для некоторых и будет справедливо 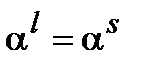, а значит, 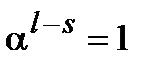. Назовем минимальное натуральное число 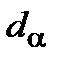, для которого

,

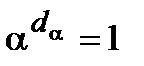мультипликативным порядком элемента 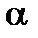. Очевидно, что только единичный элемент любого конечного поля обладает мультипликативным порядком, равным единице, т.е. .

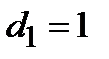Следующая теорема, приводимая без доказательства, утверждает, что значения мультипликативных порядков элементов поля подчиняются достаточно строгому ограничению.

Теорема 2.5.1.Мультипликативный порядок любого ненулевого элемента 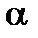поля 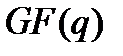делит 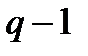, т.е. число ненулевых элементов поля .

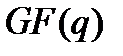Элемент 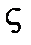поля 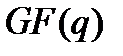, имеющий максимальный мультипликативный порядок 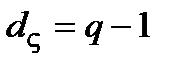, называется примитивным элементом поля.

В любом конечном поле 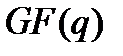всегда существует хотя бы один примитивный элемент 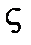. Отличительной особенностью данного элемента является то, что все его 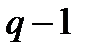последовательных степеней 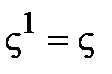, 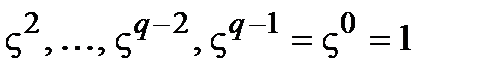различны и пробегают все ненулевые элементы поля .

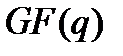Утверждение 2.5.1.Если мультипликативный порядок элемента 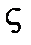равен 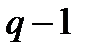, то порядок элемента 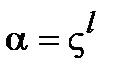определяется как

,

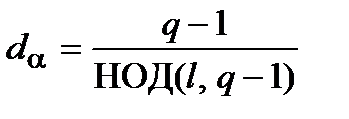где 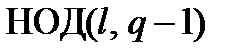– наибольший общий делитель .

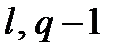Утверждение 2.5.2.В любом поле 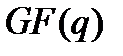содержится 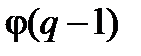примитивных элементов, где 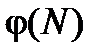– функция Эйлера, указывающая число целых чисел из диапазона от 1 до 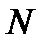, взаимно простых с .

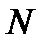Расширенное поле, построенное как множество полиномов по модулю некоторого неприводимого полинома, всегда содержит в качестве элемента поля полином 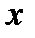. Если окажется, что 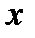– примитивный элемент, то соответствующий неприводимый полином называется примитивным полиномом. Примитивные полиномы произвольной степени 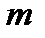определены над любым конечным полем. Они являются полезным инструментом для построения расширенных полей, поскольку позволяют реализовать очень простой вариант таблицы умножения элементов поля. Действительно, любые ненулевые элементы 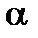и 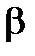расширенного поля 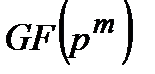могут быть выражены как некоторые 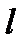–я и 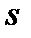–я степени примитивного элемента 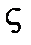: 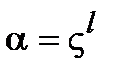, 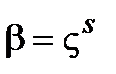. Тогда 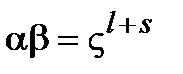и, значит, таблица умножения двух элементов поля 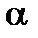и 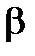представляет собой ни что иное, как все не нулевые степени примитивного элемента.

Таким образом, построение расширенного поля 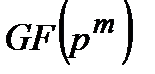в виде степеней примитивного элемента предполагает следующий алгоритм действий. На первом этапе выбирается некоторый примитивный полином степени 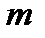над основным полем 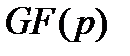, которые содержатся в специальных таблицах: 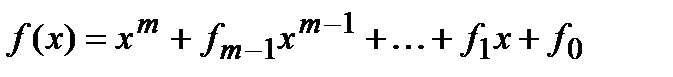. Тогда 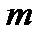–я степень 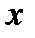по модулю 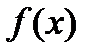определится как 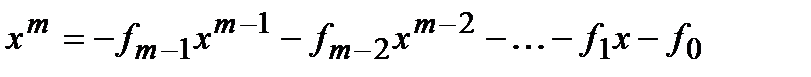. Предположение о примитивности 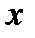позволяет задать 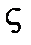в виде 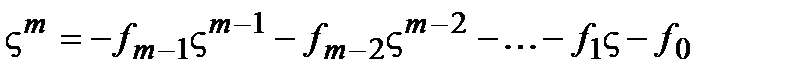. Отсюда

.

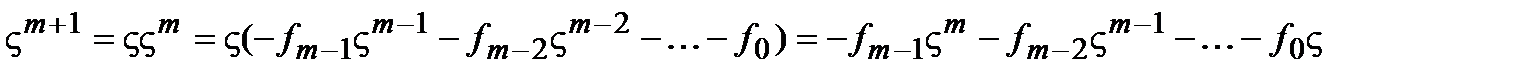Учитывая, что 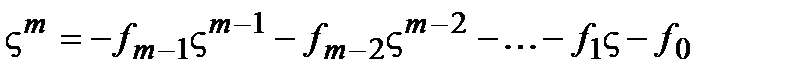и подставляя его в последнее соотношение, получаем в явном виде выражение для 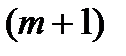–й степени 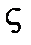. Последовательное возведение в степень 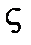позволяет, таким образом, определить все ненулевые элементы расширенного поля в виде линейной комбинации первых 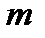степеней 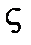: 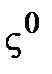, , 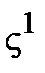…, 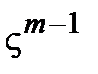с коэффициентами из основного поля .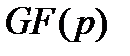