Корректирующая способность кода

Для того, чтобы дать наглядное, геометрическое толкование процедуры различения сигналов, введем понятие расстояния Хэмминга.

Расстояние Хэмминга , определяется как число позиций, в которых кодовые символы двух слов отличаются друг от друга.

Данная характеристика показывает, насколько удалены сигналы друг от друга, что играет определяющую роль в теории информации в целом. Чем больше расстояние между сигналами, тем меньше вероятность перепутывания переносимой ими информации.

Для расстояния Хэмминга выполняются следующие три аксиомы:

– симметрии – ;

– неотрицательности – , причем если , то ;

– неравенства треугольника – .

Наряду с расстоянием Хэмминга широко используется такая характеристика, как вес Хэмминга . Весом Хэмминга вектора называется число его ненулевых компонент. Очевидно, что и , где под суммированием векторов понимается покомпонентное сложение.

Пример 1.4.1.Для двух двоичных векторов и расстояние Хэмминга , поскольку символы, стоящие на второй, третьей и пятой позиций различаются, а на первой и четвертой – совпадают. В свою очередь вес Хэмминга для указанных векторов составляет величину и .

Теорема 1.4.1.Код исправляет любые ошибки кратности и менее в том и только в том случае, если кодовое расстояние удовлетворяет неравенству

. (*)

Доказательство:

Достаточность:Пусть имеется код 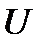с кодовым расстоянием . Предположим, что произошла ошибка кратности , и что найдутся два кодовых вектора и такие, что

,

а значит, не позволяющие исправить ошибку кратности . Однако, как следует из аксиом расстояния,

,

X2

X1

X3

XM

Y

t

d(Y,X3)£t

Рис. 1

что противоречит условию теоремы. Следовательно, неравенство (*) определяет достаточное условие исправление ошибок кратности и менее.

Необходимость:С другой стороны, если , то обязательно возникнет ситуация, при которой произойдет неверное декодирование. Например, если , то существует такой вектор наблюдения 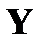, для которого , и, следовательно, наблюдается неопределенность в принятии решения. Таким образом, условие (*) является необходимым.

Полезной иллюстрацией приведенного доказательства может служить диаграмма, представленная на рис. 1. На ней изображены сферы Хэммингарадиуса c центром , представляющие собой множество точек (векторов), расположенных от на расстоянии Хэмминга или ближе. Если все сферы Хэмминга радиуса , окружающие кодовые вектора , не перекрываются, декодер воспримет любой вектор внутри i–ой сферы, как i–ый кодовый вектор . Это означает, что любая ошибка кратности и менее в кодовом слове будет исправлена. Вместе с тем, при условии исправления любых ошибок кратности избежать перекрытия сфер можно только в том случае, если минимальное расстояние Хэмминга между кодовыми векторами не меньше, чем .

Из представленной диаграммы легко увидеть, что обнаружение ошибок кратности в принятых векторах возможно тогда, когда выполняется условие

.

Из рассмотренного видно, что основными параметрами блокового кода являются: кодовое расстояние 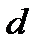, его объем 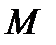и длина 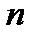. Часто при описании характеристик кода вместо объема 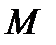используют либо число информационных символов в кодовом слове , либо скорость кода . Именно с этими параметрами связаны два основных варианта задач, рассматриваемых теорией кодирования. Первая из них связана с максимизацией 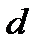при заданных значениях 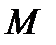( или ) и 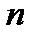для достижения хорошей корректирующей способности кода. Дуальной задачей является максимизация ( или 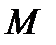) при минимуме 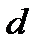и длины .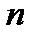