Метод линеаризации экспериментальных кривых
При малом объеме эмпирических данных, полученных в опыте (хi0, yi0), линейность кривой регрессии предварительно проверяют графически, то есть путем нанесения экспериментальных точек на график в координатах х0, y0 (индекс «0» обозначает в данном случае – «опытные», а не показатель степени). Если визуальная оценка подтверждает линейность ожидаемой зависимости, то в качестве изучаемых величин x, y оставляют экспериментальные значения, непосредственно определенные в опытах, то есть x = х0; у = y0.
Если экспериментальные точки (по визуальной оценке) лучше группируются не около прямой, а около некоторой воображаемой кривой, то следует произвести предварительную линеаризацию полученной кривой путем перехода к другим осям координат. В простейшем случае такая процедура заключается в следующем. Система осей заменяется на логарифмическую или полулогарифмическую с введением новых величин х = ℓg х0; у = ℓg y0. В этом случае в качестве изучаемых величин принимаются полученные таким образом значения x, y.
2.3. Организация опытов и анализ результатов массового эксперимента (на примере исследования твердости)
Механические испытания и использование
Корреляционного анализа
В табл. 2.4 приведены результаты экспериментального определения прочностных характеристик серии предлагаемых для исследования деталей (образцов). Дополните таблицу результатами, полученными вами, и установите в итоге окончательный объем выборки, то есть число n.
Таблица 2.4
Основные прочностные характеристики детали
| Номер образца | Предел пропорциональности | Предел текучести | Временное сопротивление | Твердость (по Роквеллу) | ||||
| σпц | ℓg σпц | σ0,2 | ℓg σ0,2 | σв | ℓg σв | HRCЭ | ℓg HRCЭ | |
| МПа | – | МПа | – | МПа | – | – | ||
| . . . |
Нанесите экспериментальные значения, полученные в опытах, на графики, принимая за аргумент х0 твердость, за функцию у0 – один из конкретных параметров прочности, то есть графики в координатах (σпц, HRCЭ), (σ0,2, HRCЭ) и (σв, HRCЭ). Визуально оцените, в каких случаях в принятых осях координат результаты можно аппроксимировать линейными зависимостями, в каких – нет. При необходимости воспользуйтесь рекомендациями, изложенными в пункте 2.2.3. Приведите в отчете поля разброса экспериментальных точек на полученных таким образом графиках (поля регрессии).
С целью определения выборочных коэффициентов корреляции прочностных параметров с твердостью (HRCЭ) используйте формулы (2.1)…(2.5) из пункта 2.2.1. Результаты расчетов удобно свести в таблицу (для примера рекомендуемая форма представлена в виде табл. 2.5).
Таблица 2.5
Пример таблицы для оформления результатов корреляционного анализа
 |  | 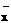 | 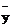 |  |  |  |  |  |
| HRCЭ | ℓg σпц | |||||||
| ℓg HRCЭ | ℓg σ0,2 | |||||||
| HRCЭ | σв |
На основании проведенного корреляционного анализа сделайте выводы об уровнях взаимосвязи (см. табл. 2.1) между каждым из исследуемых прочностных параметров и твердостью детали.
Для проверки нулевой гипотезы (см. пункт 2.2.1 – текст, набранный курсивом) используйте преобразование Фишера и его анализ согласно выражениям (2.6)…(2.9). Уровень значимости (α) задается или принимается самостоятельно. Обоснуйте правомерность своих выводов и дайте им вероятностную трактовку (на основании проверки нулевой гипотезы).
