Уровни взаимосвязи между случайными величинами

Модуль коэффициента корреляции	Взаимосвязь между исследуемыми величинами
0,00 £ | r | < 0,20	Связи практически нет
0,20 £ | r | < 0,50	Существует слабая связь
0,50 £ | r | < 0,75	Существует средняя связь
0,75 £ | r |< 0,95	Существует сильная связь
0,95 £ | r | £ 1,00	Связь практически функциональная

При анализе результатов механических испытаний в случае малой выборки (число испытаний, то есть выборка n ≤ 50) при линейной зависимости между нормально распределенными случайными величинами в качестве количественной оценки тесноты связи между этими величинами используют выборочный коэффициент корреляции r_о

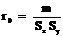. (2.1)

Здесь выборочный смешанный центральный момент

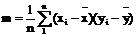, (2.2)

где 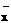, 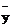– выборочные средние экспериментальных величин x_i , y_i :

,

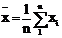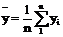. (2.3)

Выборочные средние квадратические отклонения:

,

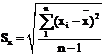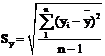. (2.4)

При малом объеме n значение выборочного коэффициента корреляции (2.1) целесообразно корректировать по формуле:

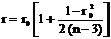. (2.5)

Выборочный коэффициент корреляции, как и другие выборочные характеристики, является случайным параметром (ввиду ограниченности n) и может принимать различные значения в пределах своего разброса, но если число опытов стремится к бесконечности, его средняя величина в пределе стремится к генеральному коэффициенту корреляции r.

При теоретическом анализе экспериментальных величин генеральный коэффициент корреляции r равен нулю в том случае, когда они независимы по природе. Однако выборочный коэффициент r, полученный в результате ограниченного числа опытов, тем не менее может отличаться от нуля. В связи с этим возникает важная практическая задача: проверка нулевой гипотезы, то есть гипотезы о равенстве нулю генерального коэффициента корреляции на основании эмпирических данных, для которых оказалось, что r ≠ 0. Дело в том, что признание генерального коэффициента корреляции равным нулю будет автоматически означать признание изучаемых величин независимыми по природе.

В начале решения такой задачи необходимо, прежде всего, установить закон распределения выборочного коэффициента корреляции, потому что при ограниченном количестве опытов он может существенно отличаться от нормального закона. При этом обычно используют пре-

образование Фишера, который показал, что распределение случайной величины

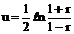(2.6)

хорошо аппроксимируется нормальным законом с математическим ожиданием

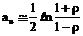(2.7)

и дисперсией 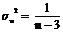. (2.8)

Проверка нулевой гипотезы, то есть гипотезы: r = 0 (при альтернативной r ≠ 0), заключается в вычислении по формулам (2.6), (2.8) значений U, σ_u и сопоставлении выборочного значения U с критическим, найденным по табл. 2.2 для вероятности 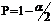( 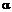– принимаемый исследователем «уровень значимости). Если

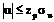, (2.9)

нулевую гипотезу принимают, т. е. r = 0. В том случае, когда 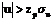, нулевую гипотезу отвергают (r ≠ 0). В условии (2.9) Z_p – значение квантили нормированного нормального распределения U *.

Таблица 2.2

Значения квантили Z_p величины U в зависимости от вероятности P

Ρ	Тысячные доли Ρ
0,80 0,81 0,82 0,83 0,84 0,85 0,86 0,87 0,88 0,89 0,90 0,91 0,92 0,93 0,94 0,95 0,96 0,97 0,98 0,99	0,842 0,879 0,915 0,954 0,994 1,036 1,080 1,126 1,175 1,227 1,282 1,341 1,405 1,476 1,555 1,645 1,751 1,881 2,054 2,326	0,849 0,885 0,922 0,962 1,003 1,045 1,089 1,136 1,185 1,237 1,293 1,353 1,419 1,491 1,572 1,665 1,774 1,911 2,097 2,409	0,856 0,893 0,931 0,970 1,011 1,054 1,098 1,146 1,195 1,248 1,305 1,366 1,433 1,506 1,589 1,685 1,799 1,943 2,144 2,512	0,863 0,900 0,938 0,978 1,019 1,063 1,108 1,155 1,206 1,259 1,317 1,379 1,447 1,522 1,607 1,706 1,825 1,977 2,197 2,652	0,871 0,908 0,946 0,986 1,028 1,071 1,117 1,165 1,216 1,270 1,329 1,392 1,461 1,538 1,626 1,728 1,852 2,014 2,257 2,878