Отношения рода и вида между понятиями.
Отношения рода и вида между понятиями.
Одно понятие может определяться через другое, и в этом случае говорят, что эти понятия находятся в отношении рода-вида. Понятие четырехугольника является родовым по отношению к понятию квадрат, а квадрат есть видовое понятие по отношению к четырехугольнику. Видовое понятие обладает всеми свойствами родового понятия. Но нельзя сказать, что родовое понятие обладает всеми свойствами видового понятия.
Следует отметить, что одно и то же понятие может быть по отношению к одному родовым, а по отношению к другому видовым. #: параллелограмм – родовое понятие по отношению к квадрату и видовое понятие по отношению к понятию четырехугольник. А также одно и то же понятие может иметь несколько родовых понятий. #, для квадрата родовыми понятиями могут быть: параллелограмм, ромб, прямоугольник.
Явные и неявные определения понятий.
Определение – это логическая операция, раскрывающая содержание данного понятия.
| Явные | Неявные | |
| Имеют форму равенства и состоят из двух частей: определяемое понятие + определяющее понятие (родовое понятие и видовое отличие). | контекстуальные это такое неявное определение понятия, при котором суть (содержание понятия) раскрывается через рассказ. | остенсивные определение понятия раскрывается через показ объектов, принадлежащих объему данного понятия. |
Примеры явных и неявных определений понятий, изучаемых в начальном курсе математики.
| Явные | Неявные | |
| Квадрат – это ромб, у которого углы прямые. Квадрат – определяемое понятие. Ромб – определяющее понятие, в котором ромб – это родовое понятие, а прямые углы – видовое отличие. | контекстуальные # Текст: к какому числу надо прибавить 6, чтобы получилось 15? Обозначим неизвестное число латинской буквой икс. x+6=15 – это уравнение. Решить уравнение – значит найти неизвестное число | остенсивные #Пример понятия равенства и неравенства. |
3 ВОПРОС:Истомина 1кл,1ч
2. Высказывания и высказывательные формы. Смысл логических связок «и», «или» в составных высказываниях. Высказывания с кванторами. Особенности формулирования высказываний с квантором общности в начальном курсе обучения математике.
Высказываниемназывается такое предположение, относительно которого имеет смысл задать вопрос, истинно оно или ложно.
Высказывательная форма–предположение, содержащее одно или несколько переменных, которое обращается высказыванием при подстановке в него вместо переменного или переменных конкретных значений. Это предложение, относительно которого не имеет смысл задавать вопрос истинно оно или ложно.
Смысл логических связок «и», «или» в составных высказываниях.
Определить истинно высказывание или ложно – это значит найти значение истинности высказывания. Высказывания бывают элементарныеи составные.Составные образуются из элементарных при помощи логических связок: и, или, если…то, не и т.д.
Значение истинности составных высказываний устанавливается по определенным правилам с помощью таблиц истинности.
Высказывание вида A ^ B (“и”) называется конъюнкцией. Высказывание вида A v B (“или”) называется дизъюнкцией.
| А | В | А V В |
| и | и | и |
| и | л | л |
| л | и | л |
| л | л | л |
Конъюнкцией высказываний А и В называется высказывание A ^ B, которое истинно, когда оба высказывания истинны, и ложно, когда хотя бы одно из этих высказываний ложно.
| А | В | А V В |
| и | и | и |
| и | л | и |
| л | и | и |
| л | л | л |
Дизъюнкцией высказываний А и В называется высказывание А v В, которое истинно, когда истинно хотя бы одно из высказываний, и ложно, когда оба высказывания ложны.
Высказывания с кванторами.
Для того, чтобы высказывательную форму преобразовать в высказывание, существуют специальные слова, называемые кванторами. Различают кванторы общности и кванторы существования.
К кванторам общности ( 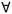 ) относятся слова: все, любой, каждый и т.д.Запись (
) относятся слова: все, любой, каждый и т.д.Запись ( 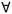 х) А(х) означает: “для всякого значения х предложение А(х) – истинное высказывание”.
х) А(х) означает: “для всякого значения х предложение А(х) – истинное высказывание”.
К кванторам существования ( 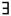 ) относятся слова: некоторые, хотя бы один и т.д. Запись (
) относятся слова: некоторые, хотя бы один и т.д. Запись ( 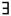 х) А(х) означает: “существует такое значение х, что А(х) – истинное высказывание”
х) А(х) означает: “существует такое значение х, что А(х) – истинное высказывание”
Примеры построения дедуктивных умозаключений с использованием этих схем.
1. Правило заключения:
# Если запись числа х оканчивается цифрой 5, то число х делится на 5 Запись числа 135 оканчивается цифрой 5. Следовательно число 135 делится на 5.
2. Правило отрицания:
# Если запись числа х оканчивается цифрой 5, то число х делится на 5. Число 177 не оканчивается цифрой 5. Следовательно, оно не делится на 5.
3. Правило силлогизма:
# Если число х кратно12, то оно кратно 6. Если число х кратно 6, то оно кратно 3. Следовательно, если число х кратно 12, то оно кратно З.
Построение умозаключения, доказывающего, например, что: «В заданном прямоугольнике противоположные стороны равны».
Для того, чтобы доказать данное утверждение строят общую посылку: если четырехугольник прямоугольный, то его противоположные стороны равны.
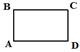
Частная посылка: ABCD – прямоугольник. Заключение: AB=CD, AD=BC
Данное рассуждение проходило по правилу заключения: (А(х) => B(x) и А(ABCD)) => B(ABCD) – верно.
5. Понятие соответствия между множествами. Взаимно однозначные соответствия. Определение числовой функции. Способы задания функций. Примеры числовых функций из начального курса математики, заданных при помощи: а) таблицы; б) выражения с переменной; в) формулы.
Примеры числовых функций из начального курса математики, заданных при помощи:
См. учебник Петерсон 4 кл. 3 ч.
а) таблицы; (стр. 70, №3 Тема: График движения)
Заполни таблицу и построй график движения Сиропчика и Незнайки.
| t ч | t | |||||
| S км |
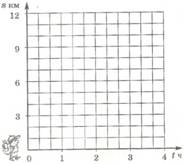
v = 3 км/ч
б) выражения с переменной; (см. учебники 4 кл.)
Вычисли значения выражений:
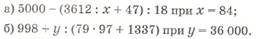
в) формулы.
Постройте график функций y=5-x, если ее область определения X такова:
- X={0,1,2,3,4,5};
- X=[0;5].
3 ВОПРОС:Персон 4 кл,3ч
6. Определения отношений на множестве. Отношения эквивалентности и их связь с разбиением множества на классы. Примеры заданий из учебников математики для начальных классов, при выполнении которых происходит разбиение на классы с помощью отношения.
Определения отношений на множестве.
Рассматриваемое отношения между двумя элементами, называется бинарным;
между тремя элементами – тернарным.
Отношениемна множестве или отношением между элементами множества называется, любое подмножество декартова произведения множества самого на себя.
Отношение – это есть множество упорядоченных пар.
Отношение обозначается заглавными буквами латинского алфавита (конечными).
| Свойства отношений: | |
| 1) Отношение R, заданное на множестве X, обладает свойством рефлексивности, если каждый элемент данного множества вступает в отношение R с самим собой. На множестве натуральных чисел рефлексивными свойствами обладают отношения кратности, равенства, делимости. |  |
| 2) Отношение R, заданное на множестве X, обладает свойством симметричности, если из того, что какой-либо элемент х из множества Х вступает в отношение R с элементом у из множества Х, следует, что элемент у вступает в отношение R с элементом х. R – равенство на множестве. | 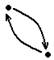 |
| 3) Отношение R, заданное на множестве X, обладает свойством антисимметричности, если для различных элементов х и у из множества X из того, что элемент х вступил в отношение R с элементом у следует, что элемент у в отношение R с элементом х не вступает. Отношения кратности, делимости, больше (меньше) на … |  |
| 4) Отношение R, заданное на множестве X, обладает свойством транзитивности, если из того, что элемент х из множества Х входит в отношение R с элементом у из множества У и элемент у входит в отношении R с элементом z из множества Х, следует, что элемент х входит в отношение R с элементом z. Отношения кратности, делимости, параллельности между прямыми. | 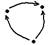 |
Уравнение первой степени с одной переменной. Равносильные уравнения. Теоремы о равносильности уравнений. Примеры уравнений из учебников математики для начальной школы и способы их решения.
Пусть f(х) и g(х) два выражения с переменной, определенные на некотором множестве Х, тогда высказывательная форма вида f(x)=g(x) называется уравнением с одной переменной. Х – область определения уравнения.
Решить уравнение - значит найти все те значения переменной х из области определения уравнения, при которых уравнение превращается в истинное числовое равенство.
Решить уравнение - значит найти множество истинности высказывательной формы f(x)=g(x).
 Два уравнения называются равносильными на некотором множестве X, если множества их решений совпадают.
Два уравнения называются равносильными на некотором множестве X, если множества их решений совпадают.
Пример:
3(х – 2) = 0 равносильные уравнения, т.к множества их решений
3х – 6 = 0 совпадают
Отрезок натурального ряда чисел и счет элементов конечного множества. Теоретико-множественный смысл натурального числа. Определение отношения «меньше» для натуральных чисел, его теоретико-множественный смысл. Примеры заданий из начального курса математики, раскрывающих теоретико-множественный смысл натурального числа и отношения «меньше».
Натуральные числа - числа, используемые при счете. Отрезком натурального ряда чисел Nа называется множество, элементами которого являются все те натуральные числа, которые меньше или равны а : Nа = {1, 2, 3, …., а} Например: отрезок N7 – это множество натуральных чисел, не превосходящих числа 7, т.е. N7 = {1, 2, 3, 4, 5, 6, 7}
Свойства отрезка натурального ряда чисел:
- каждый отрезок натурального ряда должен содержать «1».
- если натуральное число х принадлежит отрезку Nа и х≠а => число, которое следует за х (х+1) будет принадлежать Nа.
(х?Nа и х≠а) => (х+1 ? Nа)
Счетом элементов множества А называется установление взаимно однозначного соответствия между элементами данного множества и отрезком натурального ряда Nа.
В результате пересчета элементов, входящих в данное множество, мы получаем число, которое можно считать характеристикой численности множества.
Взаимно однозначным соответствием между элементами множества X и элементами множества Y называется такое соответствие, при котором каждому элементу из множества X соответствует единственный элемент из множества Y и каждый элемент их множества Y соответсвует единственному элементу из множества Х
Множества называются равномощными, если между ними можно установить взаимно однозначное соответствие.
Множество является конечным, если оно равномощно некоторому отрезку натурального ряда чисел Nа.
Правила счета:
1) Любой элемент из множества может быть назван первым при счете, т.е. пересчитывать элементы можно в любом порядке.
2) Никакой элемент не должен быть пропущен при счете, т.е. должен быть просчитан.
3) Каждый элемент при счете должен быть просчитан только один раз.
Любое натуральное число при счёте носит количественный (количество просчитанных элементов) и порядковый (показано, какой элемент был просчитан под этим номером) смысл.
Теоретико-множественный смысл суммы натуральных чисел. Свойства сложения, их теоретико-множественный смысл. Словесные формулировки свойств сложения, изучаемых в начальной школе. Примеры заданий из начального курса математики, раскрывающих теоретико-множественный смысл суммы натуральных чисел.
Сложение целых неотрицательных чисел связано с объединением конечных непересекающихся множеств. Например, если множество А содержит 5 элементов, а множество В – 4 элемента и пересечение множеств А и В, пусто, то число элементов в их объединении равно сумме 5 + 4.
Теорема. Пусть А и В — конечные множества, не имеющие общих элементов. Тогда их объединение тоже конечно, причем n(A и B) =п(А) + n(B). Доказательство. Докажем сначала, что если a и b натуральные числа, то существует взаимно-однозначное отображение отрезка натурального ряда Nа на множество X таких чисел, что а + 1 =<х=<а + b. Действительно, если поставить в соответствие числу с ? Nb число с + а, то в силу монотонности сложения этим будет задано взаимно однозначное отображение отрезка Nb на множество X. Например, если а = 3, b = 5, то соответствие между множествами N5 и X = {4, 5, 6, 7, 8} может быть установлено так: числу с ? N5 сопоставим число х = 3 + с; числу 1 - число 3 + 1=4, числу 2 - число 3 + 2 = 5 и т.д., числу 5 - число 2 + 5 = 8.
Пусть п (А) = а, п (В) = b. Тогда существуют взаимно однозначные отображения А на Nа и В на Nb. Но согласно доказанному выше, отрезок Nb можно взаимно однозначно отобразить на множество X таких чисел, что а + 1 <х<а + Ъ. Тем самым множество В взаимно однозначно отображается на X. Отображая взаимно-однозначно множество А на Na, множество В на X, получаем взаимно - однозначное отображение множества А объедин. В на отрезок Na+b Поскольку нет элементов, одновременно принадлежащих А и В, то это отображение определено на всем множестве А объедин. В. Значит, в множестве А объедин. В имеется а +b элементов, что и требовалось доказать. Из рассмотренной теоремы следует, что
Теоретико-множественных позиций сумма натуральных чисел а и в представляет собой число элементов в объединении конечных непересекающихся множеств А и В таких, что а = n(A), b = n(B): а + в = n(A) + n(B) = n(A È B), если А Ç В = Æ.
Определение вычитания натуральных чисел через сложение. Теоретико-множественный смысл разности натуральных чисел. Условие существования разности в множестве натуральных чисел. Правила вычитания числа из суммы и суммы из числа. Примеры заданий из начального курса математики, раскрывающих теоретико-множественный смысл разности натуральных чисел.
Натуральные числа — числа, возникающие естественным образом при счёте (как в смысле перечисления, так и в смысле исчисления).
Разность целых не отрицательных чисел а - в, называется такое целое неотрицательное число, что: а = в + с.
8 – 6 = 2 т. к. 6 + 2 = 8
С теоретико-множественной позиции разность натуральных чисел a и b представляет собой число элементов в дополнении множества B до множества A, если а = n(A), (целое неотрицательное число определяющее число элементов в множестве А) b = n(B) (целое неотрицательное число определяющее число элементов в множестве В) и BСA (Множество В, является подмножеством множества А).
а = n(A)
 b = n(B)
b = n(B)
 BСA
BСA
а – в = n(B\A)
Пример:
7 – 2 = n(B\A) = 5
7 = n(A)
2 = n(B)
BСA
Условие существования разности натуральных чисел: разность натуральных чисел a и b существует тогда и только тогда, когда b 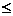 a и эта разница единственна.
a и эта разница единственна.
Правило вычитания числа из суммы и суммы из числа, их теоретико-множественная интерпретация.
Взаимосвязь вычитания чисел и вычитание множеств позволяет обосновать выбор действия. Чтобы узнать, насколько одно число меньше или больше другого, надо из большего числа вычисть меньшее.
Взаимосвязь действий над числами, теоретико-множественный смысл отношений «меньше на и больше на» позволяют обосновывать выбор действий при решении задач с этими отношениями.
1. Вычитание числа из суммы:
Правило вычитания числа из суммы: чтобы вычесть число из суммы достаточно вычесть это число из любого слагаемого и полученному результату прибавить оставшееся слагаемое(другое, которое еще не задействовано).
Теор.множ.трактовка этого правила:
Для трех конечных мн-в А, В и С, таких, что а=n(А), в=n(В) и с=n(С), A 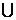 B= Ø, С
B= Ø, С 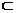 А
А
имеет место равенство: (А U В) \ С=(А\С) В, из этого следует, что число элементов в этой разности n((А 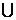 В) \ С) равно разности элементов из объединения – число элементов во мн-ве С: n((А
В) \ С) равно разности элементов из объединения – число элементов во мн-ве С: n((А 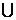 В) \ С)=n(А\C)
В) \ С)=n(А\C) 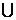 B) = (а+в)-с=(а-с)+в n(А\C)+n(В) = (а-с)+в
B) = (а+в)-с=(а-с)+в n(А\C)+n(В) = (а-с)+в
2.Вычитание суммы из числа:
a - (b + c) = a - b - c (при а >= b + c)
Для того, чтобы вычесть сумму из числа, можно сначала вычесть из этого числа первое слагаемое, а потом из полученной разности - второе слагаемое.
Теоретико-множественная интерпретация правила вычитания суммы из числа: для трёх конечных множеств А, В, С таких, что a=n(A), b=n(B), c=n(C), B 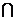 C=
C= 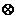 , B
, B 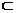 A и C
A и C 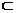 A, тогда имеет место равенство: A\(B
A, тогда имеет место равенство: A\(B 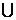 C)=(A\B)\C) из этого следует, что: n(A\(B
C)=(A\B)\C) из этого следует, что: n(A\(B 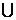 C))=n(A)\n(B
C))=n(A)\n(B 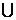 C)=n(A)- n(B
C)=n(A)- n(B  C)=a-(b+c)
C)=a-(b+c)
1. Если из числа вычесть нуль, оно не изменится.
2. Если из числа вычесть это число, получится нуль.
3 ВОПРОС:Истомина 1 кл.1ч.с,88
Определение умножения натуральных чисел через сложение. Теоретико-множественный смысл произведения. Свойства умножения. Словесные формулировки свойств умножения, изучаемых в начальной школе. Примеры заданий из начального курса математики, раскрывающих теоретико-множественный смысл умножения натуральных чисел.
Натуральные числа — числа, возникающие естественным образом при счёте (как в смысле перечисления, так и в смысле исчисления).
Определение деления натуральных чисел через умножение. Теоретико-множественный смысл частного натуральных чисел. Условие существования частного натуральных чисел. Правило деления суммы на число. Примеры заданий из начального курса математики, раскрывающих теоретико-множественный смысл частного.
Натуральные числа — числа, возникающие естественным образом при счёте (как в смысле перечисления, так и в смысле исчисления).
Частным натуральных чисел а и b называется такое число с, что а=b*с.
Натуральное число как результат измерения положительной скалярной величины. Смысл суммы и разности натуральных чисел, полученных в результате измерения величин. Примеры заданий из начального курса математики, раскрывающих смысл суммы и разности натуральных чисел – мер величин.
ПЕРЕСЕЧЕНИЕ
Пересечением множеств А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству А и множеству В.
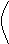

 Пересечение множеств А и В обозначают А Ç В. Таким образом, по определению, А ÇВ = {х / xÎA и xÎ В].
Пересечение множеств А и В обозначают А Ç В. Таким образом, по определению, А ÇВ = {х / xÎA и xÎ В].
Если изобразить множества А и В при помощи кругов Эйлера, то пересечением данных множеств является заштрихованная область
В том случае, когда множества А и В не имеют общих элементов, говорят, что их пересечение пусто и пишут: А ÇВ =Æ.
Примеры:
| Если элементы множеств А и В перечислены, то, чтобы найти А Ç В, достаточно перечислить элементы, которые одновременно принадлежат множеству А и множеству В, т.е. их общие элементы. | Пересечение множества А - четных натуральных чисел и множества В — двузначных чисел. Тогда, согласно определению, элементы пересечения данных множеств должны обладать свойством «быть четными натуральными и двузначными числами». Таким образом, множество А Ç В состоит из четных двузначных чисел. Полученное множество не пусто. Например, 24 Î А Ç В, поскольку число 24 четное и двузначное. |
ОБЪЕДИНЕНИЕ

 Объединением множеств А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству А или множеству В.
Объединением множеств А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству А или множеству В.
Объединение множеств А и В обозначают А ÈВ. Таким образом, по определению, А ÈВ = {х \ х ÎА или х Î В].
при помощи кругов Эйлера, то объединение данных множеств изобразится заштрихованной областью.
Примеры:
| Если элементы множеств А и В перечислены, то, чтобы найти А È В, достаточно перечислить элементы, которые принадлежат множеству А или множеству В. | Найдем объединение множества А - четных натуральных чисел и множества В - двузначных чисел. В объединение данных множеств войдут числа, характеристическое свойство которых - «быть четным натуральным или двузначным числом».Такие числа образуют бесконечное множество, но сформулированное характеристическое свойство позволяет однозначно определять, содержится тот или иной элемент в объединении множеств А и В или не содержится. Например, в А ÈВ есть число 8, поскольку оно четное; есть число 36 - оно четное и двузначное. |
РАЗНОСТЬ
ДОПОЛНЕНИЕ
Пусть В Ì А. Дополнением множества В до множества А называется множество, содержащее те и только те элементы множества А, которые не принадлежат множеству В.
Из определения следует, что В'а = {х | х Î А и х Ï В}.
ПРИМЕРЫ:
| Если элементы множеств А и В перечислены и В с А, то, чтобы найти дополнение множества В до множества А, достаточно перечислить элементы, принадлежащие множеству А и не принадлежащие множеству В. Так, если А = {1,2,3,4,5}, а В = {2, 4}, то В`а = {1,3, 5). | Так, если А - множество четных чисел, а В - множество чисел, кратных 4, то в'а -это множество, содержащее такие четные числа, которые не делятся на 4. Например, 22 Î в'а , т.к. 22 Î А (т.е. оно четное) и 22 Ï В (т.е. оно не кратно 4). |
ПРИМЕРЫ ИЗ НАЧАЛЬНОЙ ШКОЛЫ:
Объединение:
а. У школы посадили 4 липы и 3 березы. Сколько всего деревьев посадили у школы?
б. У Коли было 6 книг. В день рождения ему подарили еще 4 книги. Сколько книг стало у Коли?
Пересечение:
а. У Коли 10 книг, 2 книги он подарил товарищу. Сколько книг осталось у Коли?
В зале было 100 стульев. После того как вынесли несколько стульев, в зале осталось 86 стульев. Сколько стульев вынесли из зала?
3 ВОПРОС:Истомина 1кл.1ч.с.70.
17. Теоретико-множественный смысл отношений "X больше (меньше) Y на а ", заданных на множестве целых неотрицательных чисел. Примеры заданий из начального курса математики, раскрывающих связь данного отношения с операциями над целыми неотрицательными числами.
В аксиоматической теории определение отношения «меньше на» («больше на») естественным образом вытекает из определения отношения «меньше».
Действительно, из того, что а < b тогда и только тогда, когда существует такое натуральное число с, что а + с = b, имеем, что «а меньше b на с» или «b больше а на с».
Итак, с теоретико-множественной точки зрения «а меньше b на с» (или «b больше а на с») означает, что если а = п(А), b = n(B), то в множестве В содержится столько элементов, сколько их в А, и еще с элементов.
Так как с = п(В\В1), где В1Ì В, п(В) = b, п(В1) = а, то, по определению разности, с = а - b.
Следовательно, чтобы узнать, на сколько одно число меньше или больше другого, надо из большего числа вычесть меньшее.
ПРИМЕРЫ ЗАДАНИЙ ИЗ НАЧАЛЬНОГО КУРСА МАТЕМАТИКИ
Взаимосвязь действий над множествами с действиями над числами, теоретико-множественный смысл отношений «меньше на» и «больше на» позволяют обосновывать выбор действий при решении задач с этими отношениями.
| Рассмотрим, например, такую задачу: «На столе 5 чашек, а ложек на 2 больше. Сколько на столе ложек?» | Рассмотрим еще одну задачу: «На столе 5 чашек, а ложек на 2 меньше. Сколько на столе ложек?» |
| Легко видеть, что она решается при помощи сложения. Почему? В задаче речь идет о двух множествах: множестве чашек (А) и множестве ложек (В). Известно, что в первом множестве 5 элементов, т.е. п(А) = 5. Число элементов во втором множестве требуется найти при условии, что в нем на 2 элемента больше, чем в первом. Отношение «больше на 2» означает, что в множестве В элементов столько же, сколько их в А, и еще 2 элемента. Применимо к тем множествам, о которых идет речь в задаче, это означает, что ложек на столе столько же, сколько чашек, и еще 2. Используя правило подсчета элементов в объединении непересекающихся множеств, получаем: n(B) = n(B1) + n(B\B1) =5+2. Так как 5 + 2 = 7, то получим ответ на вопрос задачи: на столе 7 ложек. | Выясним, почему она решается при помощи вычитания. В задаче речь идет о двух множествах: множестве чашек (А) и множестве ложек (В). Известно, что в первом множестве 5 элементов, т.е. п(А) - 5. Число элементов во втором множестве надо найти при условии, что в нем на 2 элемента меньше, чем в первом. Отношение «меньше на 2» означает, что в множестве В элементов столько же, сколько их в А, но без двух. Применимо к тем множествам, о которых идет речь в задаче, это означает, что ложек на столе столько же, сколько чашек, но без двух. Таким образом, п (В) = п(А1) = п(А)-п(А\А1) =5-2. Так как 5 - 2 = 3. то получим ответ на вопрос задачи: на столе 3 ложки. |
3 ВОПРОС:Истомина 1кл.2ч.с.11. Рудницкая 3кл.2ч. с.4
Позиционные и непозиционные системы счисления. Особенности десятичной системы счисления. Правило установления отношений «равно», «меньше», «больше» для чисел, записанных в этой системе. Примеры заданий из начального курса математики, при выполнении которых младшие школьники знакомятся с особенностями десятичной системы счисления.
Язык для наименования, записи чисел и выполнения действий над ними называют системой счисления.
Называть числа и вести счет людям помогали пальцы рук и ног, верёвочные узлы, зарубки. Но это слишком долго, поэтому счет стали вести группами, состоящими из одинакового числа элементов. Наряду с группами по 10 элементов встречались группы по 5, 12, 20 элементов. В Древнем Вавилоне считали группами по 60 единиц. Древневавилонская система используется до сих пор при измерении времени и углов в минутах и секундах.
Наибольшее распространение получила десятичная система записи чисел. Эта система, принятая сейчас почти всюду, основана на группировании десятками и берет свое начало от счета на пальцах. (Возникла в Индии, первыми её заимствовали арабы).
Различают позиционные и непозиционные системы счисления.
В позиционных системах один и тот же знак может обозначать различные числа в зависимости от места (позиции), занимаемого этим знаком в записи числа. Так, шестидесятеричная вавилонская и десятичная системы счисления являются позиционными.
Непозиционные системы характеризуются тем, что каждый знак (из совокупности знаков, принятых в данной системе для обозначения чисел) всегда обозначает одно и то же число, независимо от места (позиции), занимаемого этим знаком в записи числа. Примером такой системы может служить римская система, возникшая в средние века. В этой системе счисления имеются знаки для узловых чисел:
· единица - I, пять - V,, десять – Х, пятьдесят - L, сто - С, пятьсот- D, тысяча- М.
Все остальные числа получаются при помощи двух арифметических операций: сложения и вычитания. Вычитание производится тогда, когда знак, соответствующий меньшему узловому числу, стоит перед знаком большего узлового числа. Например, IV - четыре, ХС - девяносто.
Запишем несколько чисел в римской нумерации.
193 - это сто (С) плюс девяносто, т.е. сто без десяти (ХС), плюс три (III); следовательно, число 193 записывается как CXCIII.
564 - это пятьсот (D) плюс пятьдесят (L) плюс десять (X) плюс четыре, т.е. пять без одного (IV). Следовательно, 564 записывается как DLXIV.
2708 - это две тысячи (ММ) плюс пятьсот (D) плюс сто (С) плюс сто (С) плюс пять (V) плюс три (III). Следовательно, число 2708 записывается так: MMDCCVIII.
Если число содержит несколько (немного) тысяч, то для его записи в римской нумерации пользуются повторением знака М. Вообще же числа четырех-, пяти- и шестизначные записывались с помощью буквы m (от лат. слова mille - тысяча), слева от которой записывали тысячи, а справа - сотни, десятки, единицы. Так, запись CXXXIIImDCCCXLII является записью числа 133842.
Римская система записи чисел была удобнее, чем зарубки на бирках, поскольку позволяли записывать большие числа. Однако выполнение действий над ними было весьма сложным делом. Поэтому на смену им пришла десятичная система счисления.
Правило установления отношений «равно», «меньше», «больше» для чисел, записанных в десятичной системе счисления.
Чтобы установить отношения «равно», «меньше», «больше»для чисел, записанных в десятичной системе счисления, необходимо определить разрядность данных чисел (если отличается, то больше то число, в котором больше разрядов). Если количество разрядов в числах совпадает, то сравнение начинается со старшего разряда.
3 ВОПРОС:Истомина 1кл.2ч.с.31. Рудницкая 3кл.1ч. с.46
Алгоритм сложения многозначных чисел в десятичной системе счисления; теоретические факты, лежащие в их основе. Примеры заданий из учебников математики для начальной школы, раскрывающих теоретические основы данного алгоритма.
В начальной школе эти алгоритмы известны под: сложением, вычитание, умножением, делением многозначных чисел в столбик.
В основе алгоритмов письменного сложения и вычитания лежат следующие теоретические положения:
1. Представление числа в десятичной системе счисления.
6145 = 6*103 + 1*102 + 4*10 + 5
Представление числа в десятичной системе счисления аналогом в начальной школе является разрядный состав числа.
2. Предлагая учащимся записать одно слагаемое под другим, а также вычитаемое, разряд под разрядом, мы тем самым раскрываем такие теоретические основы данных алгоритмов, как коммутативно-ассоциативное свойство сложения, а также правило вычитания числа из суммы и суммы из числа.
3. В основе сложения и вычитания многозначных чисел также лежит дистрибутивный закон умножения относительно сложения и вычитания соответственно.
4. Общее положение лежащее в основе данных письменных вычислительных алгоритмов – табличные случаи сложения однозначных чисел.
451 + 237 (представление чисел в десятичной системе счисления) ===
=== (4*102 + 5*10 + 1) + (2*102 + 3*10 + 7) (ассоциативный и коммутативный законы) === (4*102 + 2*102) + (5*10 + 3*10) + (1+7) (дистрибутивный закон умножения относительно сложения) === (4+2)*102 + (5+3)*10 + (1+7) (табличное сложение) === 6*102 + 8*10 + 8 (представление числа в десятичной системе счисления) === 688.
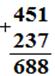
Для того, чтобы упростить указанную запись, представим эту запись "в столбик".
Алгоритм письменного сложения многозначных чисел:
1. Записываем второе слагаемое под первым строго разряд под разрядом.
2. Сложение начинаем с разряда единиц: число единиц второго слагаемого прибавляем к числу единиц первого слагаемого.
Если полученный результат < 10, записываем его в разряд единиц суммы и переходим к сложению в следующем разряде.
Если полученный результат >= 10, то представляем его в виде 10 + c, где с – однозначное число. С записываем в разряд единиц суммы, увеличивая одновременно число единиц в разряде первого десятка на 1.
3. Повторяем один из процессов.
4. Сложение считаем законченным после того, как сложены единицы старших разрядов.
3 ВОПРОС:Рудницкая 3кл.1ч. с.46
Алгоритм умножения многозначных чисел в десятичной системе счисления; теоретические факты, лежащие в его основе. Примеры заданий из учебников математики для начальной школы, раскрывающих теоретические основы данного алгоритма.
Кроме алгоритмов письменного сложения и вычитания, изучаемых в курсе математики в начальной школе, также изучается алгоритм письменного умножения многозначных чисел в десятичной системе счисления.
Алгоритм письменного умножения многозначных чисел подразделяется на следующие этапы:
1. умножение многозначного числа на однозначное
2. умножение многозначного числа на степень числа 10
3. сложение многозначных чисел
В основе алгоритма письменного умножения многозначного числа на однозначное лежат следующие положения:
- представление числа в десятичной системе счисления
- свойство действий умножения и деления
- табличное умножение однозначных чисел
Рассмотрим указанные теоретические положения на конкретном примере: 231* 3 (представление числа в десятичной системе счисления) = (2 * 102 + 3 * 101 + 1) * 3 (дистрибутивный закон умножения относительно сложения) = (2 * 102) * 3 + (3 * 10) * 3 + 1 * 3 (коммутативный и ассоциативный законы умножения) = (2 * 3) * 102 + (3 * 3) * 10 + 1 * 3 (табличное умножение однозначных чисел) = 6 * 102 + 9 * 10 + 3 (представление числа в десятичной системе счисления) = 693.
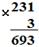 Для того, чтобы упростить указанную запись, которая представляет собой алгоритм письменного умножения многозначного числа на однозначное, предлагается представить эту запись в следующем виде, называя его письменным у
Для того, чтобы упростить указанную запись, которая представляет собой алгоритм письменного умножения многозначного числа на однозначное, предлагается представить эту запись в следующем виде, называя его письменным у
