Применение дифференциального исчисления
К исследованию функций одной переменной
Монотонность:Если производная дифференцируемой функции положительна (отрицательна) внутри некоторого промежутка 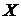 , то функция возрастает (убывает) на этом промежутке.
, то функция возрастает (убывает) на этом промежутке.
Заметим, что необходимое условие монотонности более слабое. Если функция возрастает (убывает) на некотором промежутке 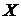 , то можно лишь утверждать, что производная неотрицательна (неположительная) на этом промежутке:
, то можно лишь утверждать, что производная неотрицательна (неположительная) на этом промежутке: 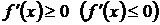 ,
, 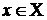 , т.е. в отдельных точках производная монотонной функции может равняться нулю.
, т.е. в отдельных точках производная монотонной функции может равняться нулю.
Практическое нахождение участков монотонности функции
Пусть функция 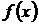 задана на
задана на 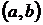 . Отметим на
. Отметим на 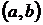 точки, в которых либо
точки, в которых либо 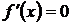 , либо
, либо 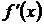 не существует, либо терпит разрыв. Пусть это точки
не существует, либо терпит разрыв. Пусть это точки 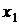 ,
, 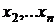 , занумерованные в порядке возрастания. На каждом из интервалов
, занумерованные в порядке возрастания. На каждом из интервалов 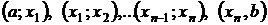 производная
производная 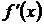 непрерывна и сохраняет знак, который совпадает со знаком
непрерывна и сохраняет знак, который совпадает со знаком 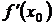 , где
, где 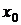 - выбранная для удобства вычислений точка этого интервала. Следовательно, на любом из этих интервалов
- выбранная для удобства вычислений точка этого интервала. Следовательно, на любом из этих интервалов 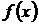 возрастает при
возрастает при 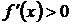 или убывает при
или убывает при 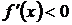 .
.
Пример № 1.
Найти интервалы монотонности функции 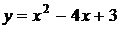 .
.
Решение.
Имеем 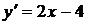 . Очевидно,
. Очевидно, 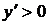 при
при 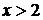 и
и 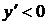 при
при 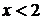 , так как:
, так как:
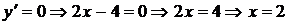 .
.
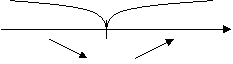
– +
2 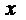
Т.е. функция убывает на интервале 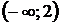 и возрастает на интервале
и возрастает на интервале 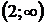 .
.
Пример № 2.
Найти интервалы монотонности функции 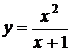 .
.
Решение.
Находим первую производную функции:
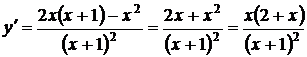 .
.
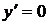 в точках
в точках 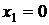 ,
, 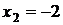 . Наносим точки на числовую прямую.
. Наносим точки на числовую прямую.
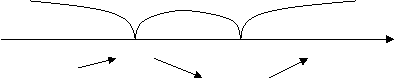 |
+ _ +
о 
-2 -1 0
В промежутках 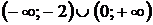 функция возрастает; а в промежутках
функция возрастает; а в промежутках 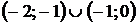 - убывает (точку
- убывает (точку 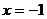 необходимо “выкалывать”, т.к. функция
необходимо “выкалывать”, т.к. функция 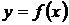 в этой точке не существует).
в этой точке не существует).
Экстремумы функции
| Определение. | Точка 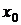 называется точкой максимума (минимума) функции называется точкой максимума (минимума) функции 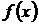 , если в некоторой окрестности точки , если в некоторой окрестности точки 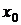 выполняется неравенство выполняется неравенство 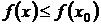 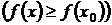 . . |
Значение функции в точке 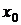 называется соответственно максимумом (минимумом) функции. Максимум и минимум функции объединяются общим названием экстремума функции.
называется соответственно максимумом (минимумом) функции. Максимум и минимум функции объединяются общим названием экстремума функции.
Экстремум функции часто называют локальным экстремумом, подчеркивая тот факт, что понятие экстремума связано лишь с достаточно малой окрестностью точки 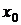 . Так что на одном промежутке функция может иметь несколько экстремумов, причем может случиться, что минимум в одной точке больше максимума в другой.
. Так что на одном промежутке функция может иметь несколько экстремумов, причем может случиться, что минимум в одной точке больше максимума в другой.
Необходимое условие экстремума:Для того чтобы функция 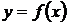 имела экстремум в точке
имела экстремум в точке 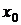 , необходимо, чтобы ее производная в этой точке равнялась нулю
, необходимо, чтобы ее производная в этой точке равнялась нулю 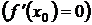 или не существовала.
или не существовала.
Точки, в которых выполнено необходимое условие экстремума, т.е. производная равна нулю или не существует, называются критическими (или стационарными).
Очень важно, однако, заметить, что обратное утверждение неверно. Критическая точка вовсе не обязательно является точкой экстремума.
Первое достаточное условие экстремума: если при переходе через критическую точку 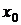 производная функции меняет свой знак с плюса на минус, то
производная функции меняет свой знак с плюса на минус, то 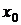 - есть точка максимума, а если с минуса на плюс, то - точка минимума.
- есть точка максимума, а если с минуса на плюс, то - точка минимума.
Схема исследования функции 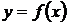 на экстремум.
на экстремум.
1. Найти ОДЗ функции 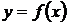 .
.
2. Найти производную 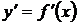 .
.
3. Найти критические точки функции, в которых производная 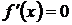 или не существует.
или не существует.
4. Исследовать знак производной слева и справа от каждой критической точки и сделать вывод о наличии экстремумов функции.
5. Найти экстремумы (экстремальные значения) функции.
Пример № 3.
Исследовать на экстремум функцию 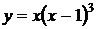 .
.
Решение.
1. ОДЗ: 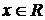 .
.
2. 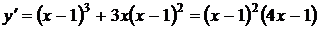 .
.
3. 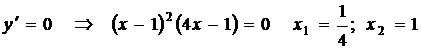 - критические точки.
- критические точки.
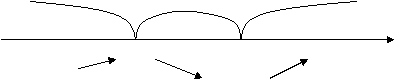
– + +
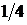 1
1 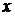
Нанести критические точки на числовую ось.
1. Согласно достаточному условию 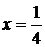 - точка минимума данной функции. В точке
- точка минимума данной функции. В точке 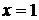 экстремума нет.
экстремума нет.
Второе достаточное условие экстремума: если первая производная 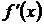 дважды дифференцируемой функции равна нулю в некоторой точке
дважды дифференцируемой функции равна нулю в некоторой точке 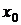 , а вторая производная в этой точке
, а вторая производная в этой точке 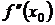 положительна, то
положительна, то 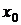 есть точка минимума функции
есть точка минимума функции 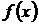 ; если
; если 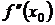 отрицательна, то
отрицательна, то 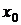 – точка максимума функции
– точка максимума функции 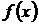 .
.
Схема исследования на экстремум функции 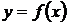 с помощью второго достаточного условия в целом аналогична схеме приведенной выше.
с помощью второго достаточного условия в целом аналогична схеме приведенной выше.
