Функции нескольких переменных
Глава XI
Функции нескольких переменных
Основные понятия
Во многих вопросах геометрии, естествознания и т. д. приходится иметь дело с функциями двух, трех переменных и более. Например, площадь треугольника 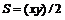 с основанием х и высотой у есть функция от двух переменных х и у, определенная в области
с основанием х и высотой у есть функция от двух переменных х и у, определенная в области 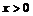 и
и 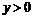 .
.
Пусть 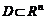 – произвольное множество точек n–мерного арифметического пространства. Если каждой точке
– произвольное множество точек n–мерного арифметического пространства. Если каждой точке 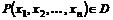 поставлено в соответствие некоторое вполне определенное действительное число
поставлено в соответствие некоторое вполне определенное действительное число 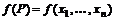 , то говорят, что на множестве D задана числовая функция f от n переменных
, то говорят, что на множестве D задана числовая функция f от n переменных 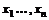 . Множество D называется областью определения, а множество
. Множество D называется областью определения, а множество 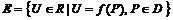 – областью значений функции
– областью значений функции 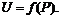
В частном случае при 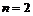 функция двух переменных
функция двух переменных  может рассматриваться, как функция точек плоскости в трехмерном геометрическом пространстве с фиксированной системой координат
может рассматриваться, как функция точек плоскости в трехмерном геометрическом пространстве с фиксированной системой координат 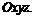 Графиком этой функции называется множество точек
Графиком этой функции называется множество точек 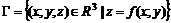 , представляющее собой, вообще говоря, некоторую поверхность в
, представляющее собой, вообще говоря, некоторую поверхность в 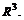
Пример.
Найти область определения функции  .
.
Решение.
Функция определена при 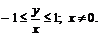
Следовательно, 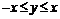 при
при 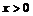 и
и 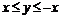 при
при 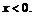
Область определения функции изображена на рис. 1 (содержит границы, за исключением начала координат).

Задачи.
11.1. Выразить площадь S треугольника как функцию длин двух его сторон x и y, если его периметр равен 2p. Найти область определения этой функции.
11.2. Выразить площадь S равнобочной трапеции как функцию длин его сторон, если x и y – длины оснований, z – длина боковой стороны. Найти область определения этой функции.
11.3.Выразить объем V прямоугольного параллелепипеда как функцию трех переменных, если длины двух его сторон основания x и y, а длина диагонали z. Найти область определения этой функции.
11.4.Выразить силу притяжения F двух материальных точек, имеющих массы m1 и m2 и занимающих соответственно положения
M(x, y, z) и M1(x1, y1, z1) как функцию шести переменных.
Найти области определения функций двух переменных:
11.5. 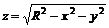 ;
;
11.6. 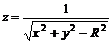 ;
;
11.7. 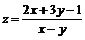 ;
;
11.8. 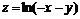 ;
;
11.9. 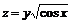 ;
;
11.10. 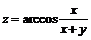 ;
;
11.11. 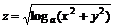 ;
;
11.12. 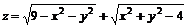 .
.
Найти область определения функций трех переменных.
11.13. 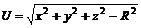 ;
;
11.14. 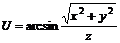 ;
;
11.15. 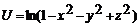 .
.
11.16. Дана функция 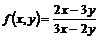 . Найти
. Найти 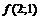 ,
, 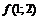 ,
, 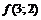 ,
, 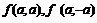 .
.
11.17. Даны функции 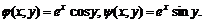
Доказать: a) 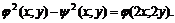
б) 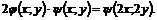
Частные производные
Пусть 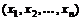 – произвольная фиксированная точка из области определения функции
– произвольная фиксированная точка из области определения функции 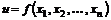 . Придавая значению переменной
. Придавая значению переменной 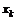 приращение
приращение 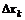 , рассмотрим предел
, рассмотрим предел
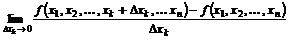 .
.
Этот предел называется частной производной данной функции по переменной 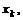 в точке
в точке  и обозначается
и обозначается 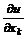 или
или 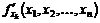 .
.
Частные производные вычисляются по обычным правилам и формулам дифференцирования (при этом все переменные, кроме 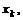 рассматриваются как постоянные).
рассматриваются как постоянные).
Пример.
Найти частные производные функции 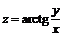 .
.
Решение.
Считая y постоянной, получим
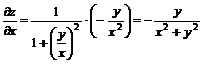 .
.
Считая x постоянной, получим
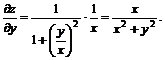
Частными производными 2–ого порядка функции 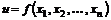 называются частные производные от ее частных производных первого порядка.
называются частные производные от ее частных производных первого порядка.
Производные второго порядка обозначаются следующим образом:
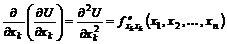 ,
,
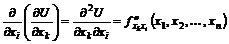 и т.д.
и т.д.
Аналогично определяются и обозначаются частные производные порядка выше второго.
Результат многократного дифференцирования функции по различным переменным не зависит от очередности дифференцирования при условии, что возникающие при этом «смешанные» частные производные непрерывны.
Пример.
Найти частные производные 2–ого порядка функции 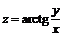 .
.
Решение.
Имеем 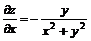 и
и 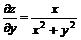 .
.
Дифференцируем вторично:
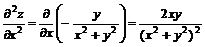 ;
;
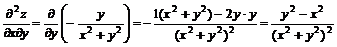 ;
;
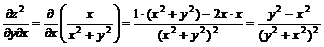 ;
;
(мы здесь убедились в том, что 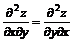 );
);
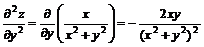 .
.
Задачи.
Найти частные производные 1–ого и 2–ого порядков от заданных функций.
11.18. 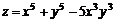 ; 11.19.
; 11.19. 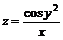 ;
;
11.20. 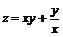 ; 11.21.
; 11.21. 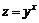 ;
;
11.22. 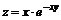 ; 11.23.
; 11.23. 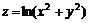 .
.
11.24. Найти 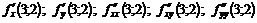 , если
, если 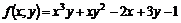 .
.
11.25. Показать, что 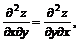 если
если 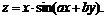
11.26. Показать, что 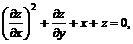 если
если 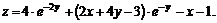
Задачи.
11.27. Найти полное приращение и дифференциал функции  если x изменяется от 2 до 2,1, а y от 1 до 1,2.
если x изменяется от 2 до 2,1, а y от 1 до 1,2.
Найти дифференциалы функций:
11.28.  ; 11.29.
; 11.29.  ;
;
11.30.  ; 11.31.
; 11.31. 
Вычислить приближенно:
11.32.  ;
;
11.33.  ;
;
11.34.  ;
;
11.35.  ;
;
11.36.  ;
;
11.37.  .
.
Задачи.
11.38. Функцию  разложить по формуле Тейлора в окрестности точки
разложить по формуле Тейлора в окрестности точки 
11.39. Функцию  разложить по формуле Тейлора в окрестности точки
разложить по формуле Тейлора в окрестности точки 
11.40. Разложить по формуле Маклорена до членов 4–го порядка включительно функцию 
11.41.Разложить по формуле Тейлора в окрестности точки (1,1) до членов 3–го порядка включительно функцию  .
.
11.42.Разложить по формуле Маклорена до членов 2–го порядка включительно функцию  .
.
Задачи.
Найти экстремумы функций двух переменных:
11.43. 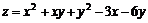 ;
;
11.44. 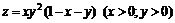 ;
;
11.45. 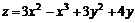 ;
;
11.46. 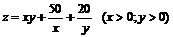 ;
;
11.47. 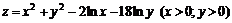 ;
;
11.48. 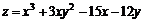 .
.
Производная сложной функции
Если  - дифференцируемая в точке
- дифференцируемая в точке 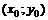 функция и
функция и 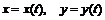 - дифференцируемые функции независимой переменной t, то производная сложной функции
- дифференцируемые функции независимой переменной t, то производная сложной функции 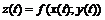 вычисляется по формуле:
вычисляется по формуле:
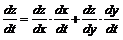 .
.
Пример.
Найти производную 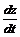 функции
функции 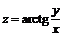 , если
, если 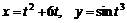 .
.
Решение.
Из предыдущего примера (см.пункт 2) имеем: 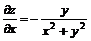 и
и 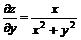 .
.
Найдем производные функций 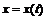 и
и 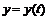 :
:
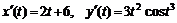 .
.
Отсюда,
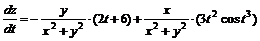 .
.
Задачи.
Найти производную 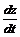 :
:
11.49. 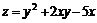 , если
, если 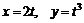 ;
;
11.50. 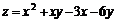 , если
, если 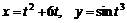 ;
;
11.51. 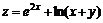 , если
, если 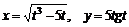 ;
;
11.52. 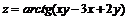 , если
, если 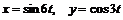 ;
;
11.53. 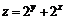 , если
, если 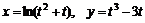 ;
;
11.54. 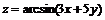 , если
, если 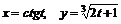 .
.
Ответы
Глава XI
11.1. 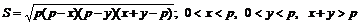 11.2.
11.2. 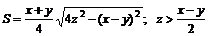 11.3.
11.3. 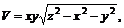
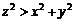 11.4.
11.4. 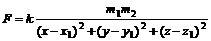 11.5.
11.5. 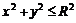 11.6.
11.6. 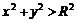 11.7.
11.7. 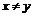 11.8.
11.8. 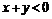 11.9.Полосы
11.9.Полосы 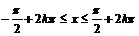 11.10.Два тупых вертикальных угла, образованных прямыми
11.10.Два тупых вертикальных угла, образованных прямыми 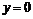 и
и 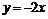 , включая границу без общей вершины (0,0)11.11.
, включая границу без общей вершины (0,0)11.11. 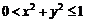 при
при 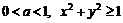 при
при 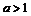 11.12.
11.12. 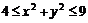 11.13.
11.13. 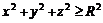 11.14.
11.14. 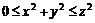 ,
,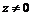 11.15.
11.15. 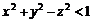 11.16.
11.16. 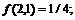
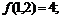
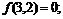
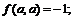
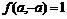 11.18.
11.18. 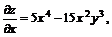
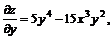
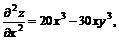
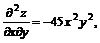
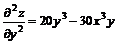 11.19.
11.19. 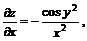
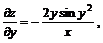
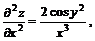
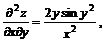
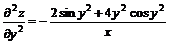 11.20.
11.20. 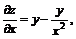
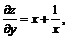
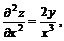
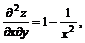
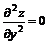 11.21.
11.21. 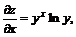
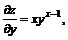
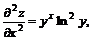
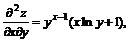
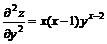 11.22.
11.22. 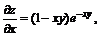
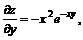
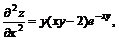
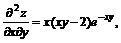
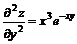 11.23.
11.23. 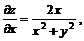
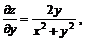
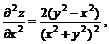
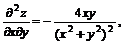
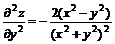 11.24.
11.24. 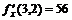 ,
, 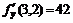 ,
, 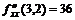 ,
, 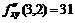 ,
, 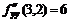 11.27.
11.27. 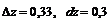 11.28.
11.28. 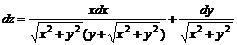 11.29.
11.29. 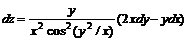 11.30.
11.30. 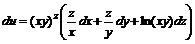 11.31.
11.31. 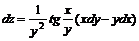 11.32.8,29 11.33.2,9511.34.0,22711.35.0,0211.36.0,03511.37.–0,0311.38.
11.32.8,29 11.33.2,9511.34.0,22711.35.0,0211.36.0,03511.37.–0,0311.38. 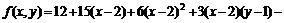
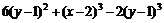 11.39.
11.39. 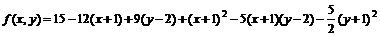
11.40. 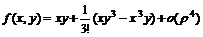 , где
, где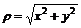
11.41. 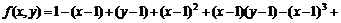
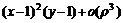 , где
, где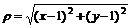 11.42.
11.42. 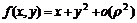 , где
, где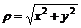 11.43.
11.43. 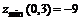 11.44.
11.44. 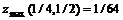 11.45.
11.45. 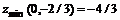 11.46.
11.46. 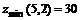 11.47.
11.47. 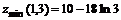 11.48.
11.48. 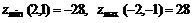 11.49
11.49 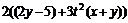 11.50.
11.50. 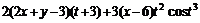 11.51.
11.51. 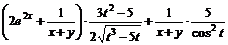 11.52.
11.52. 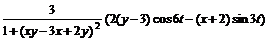 11.53.
11.53. 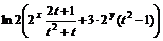 11.54.
11.54. 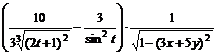 .
.
Глава XI
Функции нескольких переменных
Основные понятия
Во многих вопросах геометрии, естествознания и т. д. приходится иметь дело с функциями двух, трех переменных и более. Например, площадь треугольника 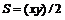 с основанием х и высотой у есть функция от двух переменных х и у, определенная в области
с основанием х и высотой у есть функция от двух переменных х и у, определенная в области 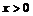 и
и 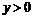 .
.
Пусть 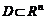 – произвольное множество точек n–мерного арифметического пространства. Если каждой точке
– произвольное множество точек n–мерного арифметического пространства. Если каждой точке 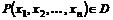 поставлено в соответствие некоторое вполне определенное действительное число
поставлено в соответствие некоторое вполне определенное действительное число 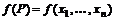 , то говорят, что на множестве D задана числовая функция f от n переменных
, то говорят, что на множестве D задана числовая функция f от n переменных 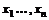 . Множество D называется областью определения, а множество
. Множество D называется областью определения, а множество 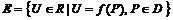 – областью значений функции
– областью значений функции 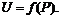
В частном случае при 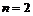 функция двух переменных
функция двух переменных  может рассматриваться, как функция точек плоскости в трехмерном геометрическом пространстве с фиксированной системой координат
может рассматриваться, как функция точек плоскости в трехмерном геометрическом пространстве с фиксированной системой координат 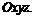 Графиком этой функции называется множество точек
Графиком этой функции называется множество точек 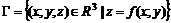 , представляющее собой, вообще говоря, некоторую поверхность в
, представляющее собой, вообще говоря, некоторую поверхность в 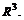
Пример.
Найти область определения функции  .
.
Решение.
Функция определена при 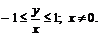
Следовательно, 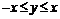 при
при 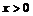 и
и 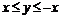 при
при 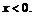
Область определения функции изображена на рис. 1 (содержит границы, за исключением начала координат).

Задачи.
11.1. Выразить площадь S треугольника как функцию длин двух его сторон x и y, если его периметр равен 2p. Найти область определения этой функции.
11.2. Выразить площадь S равнобочной трапеции как функцию длин его сторон, если x и y – длины оснований, z – длина боковой стороны. Найти область определения этой функции.
11.3.Выразить объем V прямоугольного параллелепипеда как функцию трех переменных, если длины двух его сторон основания x и y, а длина диагонали z. Найти область определения этой функции.
11.4.Выразить силу притяжения F двух материальных точек, имеющих массы m1 и m2 и занимающих соответственно положения
M(x, y, z) и M1(x1, y1, z1) как функцию шести переменных.
Найти области определения функций двух переменных:
11.5. 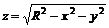 ;
;
11.6. 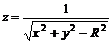 ;
;
11.7. 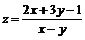 ;
;
11.8. 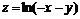 ;
;
11.9. 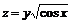 ;
;
11.10. 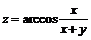 ;
;
11.11. 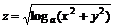 ;
;
11.12. 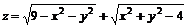 .
.
Найти область определения функций трех переменных.
11.13. 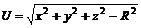 ;
;
11.14. 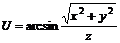 ;
;
11.15. 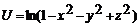 .
.
11.16. Дана функция 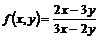 . Найти
. Найти 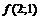 ,
, 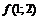 ,
, 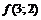 ,
, 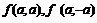 .
.
11.17. Даны функции 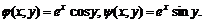
Доказать: a) 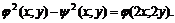
б) 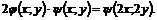
Частные производные
Пусть 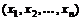 – произвольная фиксированная точка из области определения функции
– произвольная фиксированная точка из области определения функции 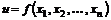 . Придавая значению переменной
. Придавая значению переменной 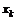 приращение
приращение 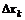 , рассмотрим предел
, рассмотрим предел
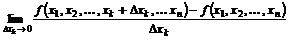 .
.
Этот предел называется частной производной данной функции по переменной 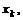 в точке
в точке  и обозначается
и обозначается 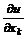 или
или 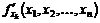 .
.
Частные производные вычисляются по обычным правилам и формулам дифференцирования (при этом все переменные, кроме 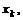 рассматриваются как постоянные).
рассматриваются как постоянные).
Пример.
Найти частные производные функции 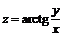 .
.
Решение.
Считая y постоянной, получим
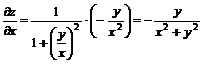 .
.
Считая x постоянной, получим
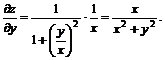
Частными производными 2–ого порядка функции 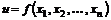 называются частные производные от ее частных производных первого порядка.
называются частные производные от ее частных производных первого порядка.
Производные второго порядка обозначаются следующим образом:
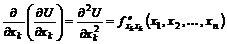 ,
,
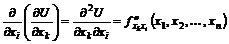 и т.д.
и т.д.
Аналогично определяются и обозначаются частные производные порядка выше второго.
Результат многократного дифференцирования функции по различным переменным не зависит от очередности дифференцирования при условии, что возникающие при этом «смешанные» частные производные непрерывны.
Пример.
Найти частные производные 2–ого порядка функции 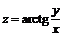 .
.
Решение.
Имеем 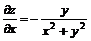 и
и 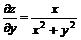 .
.
Дифференцируем вторично:
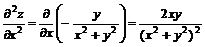 ;
;
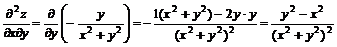 ;
;
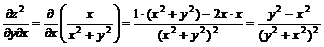 ;
;
(мы здесь убедились в том, что 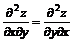 );
);
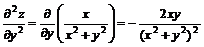 .
.
Задачи.
Найти частные производные 1–ого и 2–ого порядков от заданных функций.
11.18. 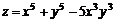 ; 11.19.
; 11.19. 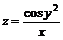 ;
;
11.20. 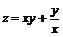 ; 11.21.
; 11.21. 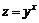 ;
;
11.22. 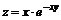 ; 11.23.
; 11.23. 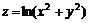 .
.
11.24. Найти 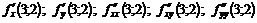 , если
, если 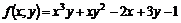 .
.
11.25. Показать, что 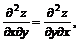 если
если 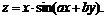
11.26. Показать, что 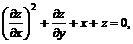 если
если