Как определяется логарифмический коэффициент затухания?

Во всякой реальной колебательной системе имеются силы сопротивления, действие которых приводит к уменьшению энергии системы. Если убыль энергии не восполняется за счет работы внешних сил, колебания будут затухать. В простейшем, и вместе с тем наиболее часто встречающемся случае, сила сопротивления 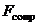пропорциональна величине скорости:

,

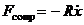где R – постоянная, называемая коэффициентом сопротивления. Знак минус обусловлен тем, что сила 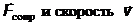имеют противоположные направления; следовательно, их проекции на ось х имеют разные знаки.

Второй закон Ньютона при наличии сил сопротивления имеет вид:

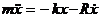
Применив обозначения: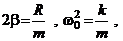

получим: 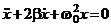- - дифференциальное уравнение затухающих гармонических колебаний.

Отметим, что 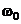представляет собой ту частоту, с которой совершались бы свободные колебания системы в отсутствие сопротивления среды (при R = 0). Эту частоту называют собственной частотой системы.

При не слишком сильном затухании (при 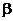< 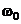) общее решение уравнения (4) имеет вид: 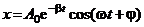, (5)

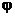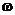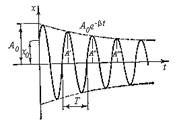
где A₀и - произвольные постоянные, - величина, определяемая формулой 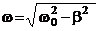. На рисунке дан график функции (5). Пунктирными линиями показаны пределы, в которых находится смещение колеблющейся точки х.

В соответствии с видом функции (5) движение системы можно рассматривать как гармоническое колебание частоты 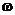с амплитудой, изменяющейся по закону:

.

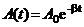Верхняя из пунктирных кривых дает график функции A(t), причем величина 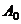представляет собой амплитуду в начальный момент времени.

Скорость затухания колебаний определяется величиной 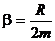, которую называют коэффициентом затухания.

Период затухания колебаний равен:

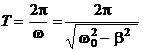(6)

При незначительном сопротивлении среды ( 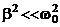) период колебаний практически не изменяется и равен 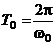. Последующие наибольшие отклонения в какую–либо сторону (например, 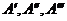и т.д. на рис.) образуют геометрическую прогрессию. Действительно, если 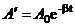, то 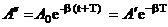, 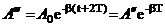и т.д.

Вообще, отношение значений амплитуд, соответствующих моментам времени, отличающимся на период, равно:

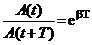
Это соотношение называется декрементом затухания, а его логарифм – логарифмическим декрементом затухания.

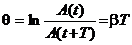. (7)

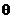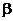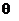Для характеристики колебательной системы обычно используется логарифмический декремент затухания . Выразив в соответствии с (7) через и 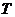, можно закон убывания амплитуды со временем записать в виде:

.

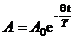Для характеристики колебательной системы часто употребляется также величина

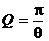, называемая добротностью колебательной системы.

Ранее мы установили, что полная энергия колеблющейся системы пропорциональна квадрату амплитуды. В соответствии с этим энергия системы при затухающих колебаниях убывает со временем по закону:

,

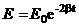где 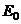- значение энергии при .

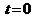Из формулы периода затухающих колебаний (6) следует, что с ростом коэффициента затухания период колебаний увеличивается. При 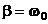период колебаний обращается в бесконечность, т.е. движение перестает быть периодическим.

При 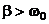решение дифференциального уравнения (5) оказывается равным сумме двух экспонент:

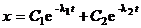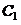, где и 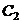- постоянные, значения которых зависят от начальных условий (от 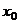и ),

,

.

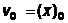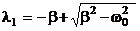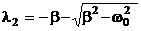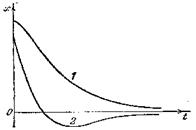
Движение в этом случае носит апериодический (непериодический) характер – выведенная из положения равновесия система возвращается в положение равновесия, не совершая колебаний.

На рисунке показано два возможных способа возвращения системы к положению равновесия при апериодическом движении. Каким из этих способов приходит система к положению равновесия, зависит от начальных условий.

47. Получите дифференциальное уравнение вынужденных гармонических колеба­ний.

48. От чего зависит амплитуда колебаний при вынужденных гармонических коле­баниях? Приведите график зависимости A(Q).

Вынужденные колебания – это колебания, которые происходят в колебательной системе под действием внешней вынуждающей силы:

,

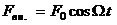где 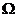- частота внешней силы.

В этом случае уравнение второго закона Ньютона имеет вид:

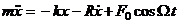
Введем обозначения

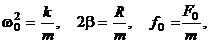
Тогда получим

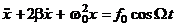- (8)

- дифференциальное уравнение вынужденных колебаний.

Это уравнение является неоднородным дифференциальным уравнением. Общее решение неоднородного уравнения равно сумме общего решения соответствующего однородного уравнения и частного решения неоднородного. Общее решение однородного уравнения мы уже знаем (см. уравнение (4) и его решение (5)).

Остается найти частное (не содержащее произвольных постоянных) решение уравнения (8). Это частное решение имеет вид:

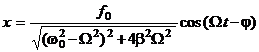, (9)

где .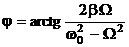

Функция (9) описывает установившиеся вынужденные колебания. Они представляют собой гармонические колебания с частотой, равной частоте вынуждающей силы. Амплитуда вынужденных колебаний

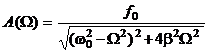(10)

пропорциональна амплитуде вынуждающей силы, а также зависит от частоты 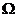вынуждающей силы. Вынужденные колебания отстают по фазе от вынуждающей силы, причем величина отставания 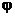также зависит от частоты вынуждающей силы.

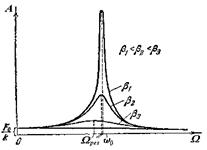На рисунке приведены графики функции 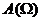при различных значениях коэффициента затухания 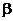. Как видно из рисунка, при некоторой определенной для данной системы частоте 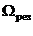амплитуда колебаний достигает максимального значения. Это явление называется резонансом, а соответствующая частота 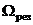- резонансной частотой. Чтобы определить резонансную частоту 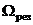, нужно найти максимум функции (10) или, что тоже самое, минимум выражения, стоящего под корнем в знаменателе.

Продифференцировав это выражение по 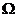и приравняв нулю, мы получим условие, определяющее :

.

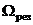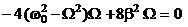Это уравнение имеет три решения: 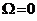и .

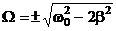Решение, равное нулю, соответствует максимуму знаменателя. Из остальных двух решений отрицательное должно быть отброшено, как не имеющее физического смысла. Таким образом, для резонансной частоты получается одно значение

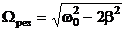. (11)

Подставив это значение частоты в (10), получим выражение для амплитуды при резонансе:

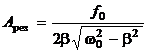. (12)

Из этого выражения следует, что при отсутствии сопротивления среды амплитуда при резонансе обращалась бы в бесконечность. Согласно (11) резонансная частота при тех же условиях (при 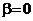) совпадает с собственной частотой колебания системы .

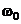Изображенная на рисунке совокупность графиков функции 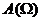, соответствующих различным значением параметра 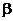, называется резонансными кривыми.

Из формулы (12) вытекает, что при малом затухании (т.е. при 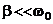) амплитуда при резонансе приближенно равна .

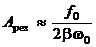Разделим это выражение на смещение 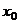от положения равновесия под действием постоянной силы ( 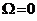), равное . В результате получим:

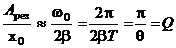
Таким образом, добротность Q показывает, во сколько раз амплитуда в момент резонанса превышает смещение системы из положения равновесия под действием постоянной силы той же величины, что и амплитуда вынуждающей силы (это справедливо лишь при небольшом затухании).

С явлением резонанса приходится считаться при конструировании машин и различного рода сооружений. Собственная частота колебаний этих устройств ни в коем случае не должна быть близка к частоте возможных внешних воздействий, т.к. в этом случае возникают вибрации, которые могут вызвать катастрофу. Вместе с тем явление резонанса часто оказывается весьма полезным, особенно в акустике, радиотехнике и т.д.

49. Получите уравнение плоской бегущей волны. Приведите график плоской бегу­щей волны.

Уравнением волны называется выражение, которое дает смещение колеблющейся частицы как функцию ее координат x, y, z и времени t:

,

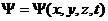где имеются в виду координаты равновесного положения частицы. Найдем вид функции 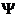в случае плоской волны, предполагая, что колебания носят гармонический характер. Для простоты направим оси координат так, чтобы ось x совпадала с направлением распространения волны. Тогда волновые поверхности будут перпендикулярными к оси x и, поскольку все точки волновой поверхности колеблются одинаково, смещение 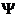будет зависеть только от x и t:

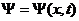
Пусть колебания точек, лежащих в плоскости 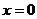, имеют вид:

.

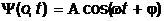Найдем вид колебания точек в плоскости, соответствующей произвольному значению x. Для того, чтобы пройти путь от плоскости 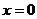до этой плоскости, волне требуется время 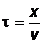, где v - скорость распространения волны. Следовательно, колебания частиц, лежащих в плоскости x, будут отставать по времени на t от колебаний частиц в плоскости 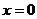, т.е. будут иметь вид:

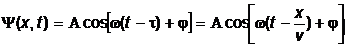
Итак, уравнение плоской волны, распространяющейся в направлении оси x, выглядит следующим образом:

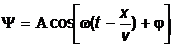
Начальная фаза волны 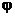определяется выбором начал отсчета x и t. При рассмотрении одной волны начала отсчета времени и координаты обычно выбираются так, чтобы 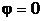. Зафиксируем какое-либо значение фазы, положив

.

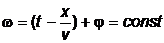Это выражение определяет связь между временем t и тем местом x, в котором фаза имеет зафиксированное значение. Вытекающее из него значение dx/dt дает скорость, с которой перемещается данное значение фазы. Продифференцировав указанное выше выражение, получим

.

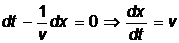Таким образом, скорость распространения волны v есть скорость перемещения фазы, в связи с чем ее называют фазовой скоростью.

Уравнению плоской волны можно придать симметричный относительно x и t вид (полагаем ):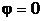

,

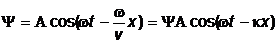где введена величина 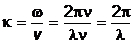, которая называется волновым числом. Таким образом

-

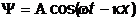- уравнение плоской бегущей волны, распространяющейся вдоль оси x,

где 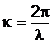- волновое число. Или

.

Теперь найдем уравнение сферической волны. Амплитуда колебаний в этом случае убывает с расстоянием от источника по закону 1/r. Тогда получим

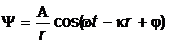- уравнение сферической волны,

где А - постоянная величина, численно равная амплитуде на расстоянии от источника, равном единице.