Разложение скорости точки на радиальную и трансверсальную компоненты

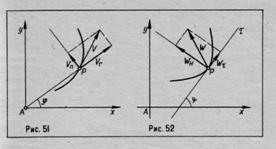
Пусть точка Р (рис. 51) движется в плоскости по какому-либо закону, А — на­чало отсчета. Требуется найти компоненты скорости: радиальную u_r (проекцию вектора скорости на ось АР) и трансверсальную (или поперечную) u_n (проекцию вектора скорости на ось, образующую с осью АР угол +p/2 радиан).

Решение. Пусть AN — действительная ось Ах, <NAP = j. В каждый момент t точка Р имеет ком­плексную координату z = re^ij (г и j — функции от t). Скорость точки Р характеризуется комплексным числом 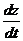(ż). Дифференцируя по обычным правилам произведение re^ij, получим:

z=re^ij+rj i e^ij. Отсюда ясно, что u_r =r, u_n=rj.

2. Разложение ускорения на тангенциальную и нор­мальную компоненты Пусть точка Р движется по неко­торой кривой Г так, что скорость точки задается в каж­дый момент t комплексным числом u=u(t) (рис. 52). Понятно, что скорость будет в течение всего движения направлена по касательной т к кривой, чего нельзя ска­зать об ускорении. Требуется найти проекции ускорения на касательную (w_i) и на нормаль (w_H) к кривой.

Эта задача аналогична предыдущей. Запишем вектор скорости в комплексной форме: z= ue^iY,

где u — абсолютная величина скорости точки Р, а Y— угол между осью Ох и касательной (Y) к кривой Г. Диф­ференцируя по переменному t, получим:

w = ż = u е^iY + uYie^iY.

Отсюда ясно, что проекция w_i вектора ускорения w на касательную ось т равна u, а проекция w_h того же векто­ра w на ось, получающуюся из оси т поворотом на

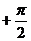радиан, равна vY: W_r = u, W_H=uy.

Широкое применение на­шли комплексные числа в картографии, электротехнике, гидродинамике, теории фильт­рации почв, теоретической фи­зике. Уже в нашем столе­тии комплексные числа и комплексные функции (функции, у которых и значениями аргумента и значениями функ­ции являются комплексные числа) успешно применялись русскими и советскими матема­тиками и механиками Н. Е. Жуковским (1847 — 1921), С. А. Чаплыгиным (1869— 1942), М. В. Келдышем (1911 — 1978) и другими в аэродина­мике. Советские математики Г. В. Колосов (1867—1936) и Н. И. Мусхелишвили (1891 — 1976) впервые стали приме­нять комплексные функции в теории упругости (то есть по существу к расчетам различ­ных конструкций на проч­ность). С применением комп­лексных переменных в теоре­тической физике связаны ис­следования советских ученых Н. Н. Боголюбова (род. 1909) и В. С. Владимирова (род. 1923).

В конце прошлого столе­тия стали широко применять генераторы переменного тока. Для расчета цепей переменно­го тока оказались непригодны­ми старые методы, разрабо­танные для цепей постоянного тока и основанные на законе Ома. В 1893 г. американский электротехник Ч. П. Штейнмец предложил эффективный метод расчета цепей перемен­ного тока. Этот метод целиком основан на применении комп­лексных чисел.

В 20-х годах нашего столетия стала разрабатываться квантовая механика. Для нее оказался особенно полезным аппарат комплексных чисел. Вот что пишет об этом изве­стный современный физик Е. Вагнер в своем очерке «Не­постижимая эффективность математики в естественных науках»: «Для неподготовлен­ного ума понятие комплексно­го числа далеко не естествен­но, не просто и никак не сле­дует из физических наблюде­ний. Тем не менее, использова­ние комплексных чисел стано­вится почти неизбежным при формулировке законов кван­товой механики. Кроме того, не только комплексным чис­лам, но и так называемым ана­литическим функциям сужде­но сыграть решающую роль в формулировке квантовой те­ории».

Для навигаторов представ­ляет значительный интерес способ построения географи­ческой карты, при котором со­храняются углы между ли­ниями. Такой способ называется конформной (то есть сохраняющей форму) проекцией. Оказывается, что с помощью функций комплексного пере­менного возможно указать бес­конечно много конформных проекций.

Значительное применение нашли комплексные числа при изучении движения есте­ственных и искусственных не­бесных тел. Приведем пример. Одна из важных задач, воз­никшая при подготовке запус­ков первых искусственных спутников Земли, состояла в следующем: как будет дви­гаться спутник под влиянием тяготения к «сплюснутому сфе­роиду» (такую форму имеет земной шар, который несколь­ко сплюснут у полюсов, его полярный диаметр примерно на 42 километра меньше эква­ториального диаметра). Одним из самых эффективных спосо­бов решения этой задачи ока­зался способ, основанный на применении комплексных чи­сел. Он был предложен совет­скими учеными Е. П. Аксе­новым, Е. А. Гребениковым и В. Г. Деминым.

ПРИЛОЖЕНИЕ 4