Построение D-оптимальной линейно-параметризованной линейно-комбинационной динамической регрессионной модели

ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА
ПРИ НЕЛИНЕЙНОЙ ПАРАМЕТРИЗАЦИИМОДЕЛИ РЕГРЕССИИ

Если модель регрессии нелинейно-параметризованная,то есть:

,

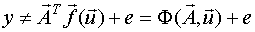то априорное планирование эксперимента невозможно, так как для нелинейно - параметризованных моделей информационная матрица Фишера и ковариационная матрица оценок зависят не только от входов, но и от неизвестных параметров модели.
В случае нелинейной параметризации возможно лишь последовательное планирование эксперимента.

Последовательное планирование эксперимента реализуется следующим образом:

1) Проводится "затравочный" эксперимент, то есть на объекте реализуется один из известных планов. При этом план должен быть невырожденным, то есть на его основе, используя метод Гаусса-Ньютона, можно найти НМНК-оценки всех неизвестных параметров модели. В результате получается начальная оценка вектора неизвестных параметров .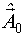

2) Планируется первый этап. Для этого синтезируемая модель раскладывается в ряд Тейлора в окрестности точки 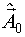. Получается линеаризованная модель. Для линеаризованной модели реализуется задача планирования эксперимента, то есть находится одна или несколько точек локального D-оптимального плана.

3) Реализуется первый этап, то есть на объекте проводятся спланированные опыты. После реализации первого этапа уточняются оценки неизвестных параметров модели методом Гаусса-Ньютона. При этом учитываются все ранее проведенные опыты (опыты "затравочного" эксперимента и опыты первого этапа).

Кроме вычисления оценок неизвестных коэффициентов вычисляется их ковариационная матрица:

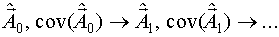
4) Планируется второй этап аналогично первому этапу. Получается линеаризованная модель в окрестности точки 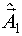, и определяется одна или несколько точек второго этапа.

5) После реализации второго этапа уточняется НМНК-оценка, то есть вычисляется 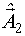с учетом всех ранее проведенных опытов. В качестве начального приближения для процедуры Гаусса-Ньютона используется оценка .

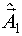Таким образом, процедура последовательного планирования представляет собой совокупность чередующихся этапов синтеза точек непрерывного, локального D-оптимального плана, их реализации на объекте и уточнения НМНК-оценок с учетом всех ранее проведенных опытов и уточняемых начальных приближений для процедуры нелинейного оценивания.

Правило останова здесь то же самое, что и для априорного планирования, то есть планирование заканчивается на том этапе, на котором отличие синтезируемого локального непрерывного плана от D-оптимального становится меньше заданного порога .

Рассмотрим формализацию процедуры для модели 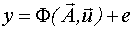. Пусть "затравочный" эксперимент включает N₀ опытов. В результате этого эксперимента найдем .

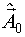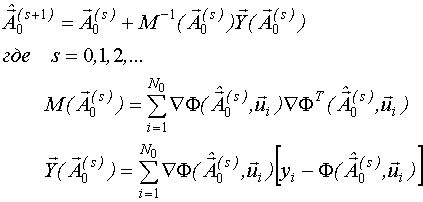
Линеаризованная модель имеет вид:

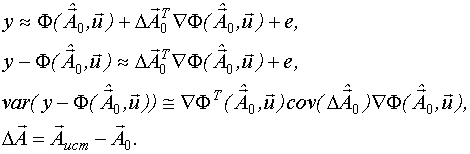
Так как 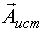неслучайная величина, то 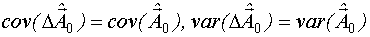, тогда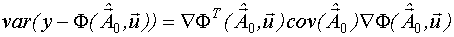

Таким образом, первая точка плана определяется как:

,

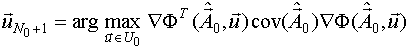где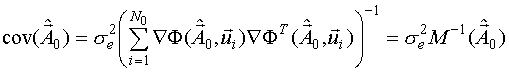

Возможно планирование сразу нескольких точек плана: 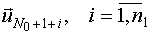, где n₁ - число экспериментов на первом этапе.

При этом необходимо воспользоваться процедурой непрерывного планирования, предполагая, что .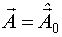

Спланированные опыты реализуется на объекте. После проведения опытов уточняется НМНК-оценка вектора 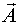. - находятся с помощью процедуры Гаусса-Ньютона. Далее планируется второй этап и т.д.

Запишем выражение для N+1-го этапа. Его осуществление производится при помощи решения следующей аргументной задачи:

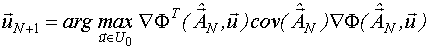
где 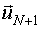- точка плана, синтезируемая на N+1 этапе.

Затем вычисляется НМНК-оценка вектора 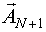по следующей формуле:

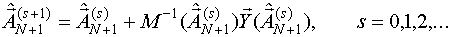
где

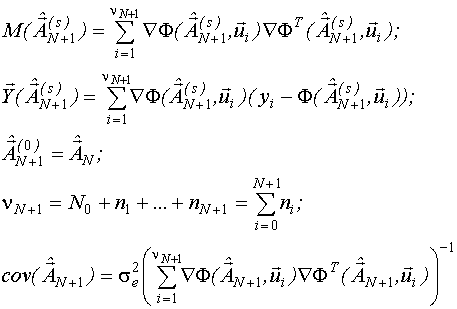
Остановка процедуры происходит на том этапе, при планировании которого отличие локального плана, состоящего из точек, полученных на всех предыдущих этапах, от D-оптимального становится меньше порогового значения .

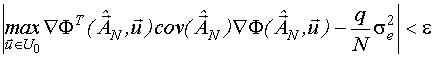
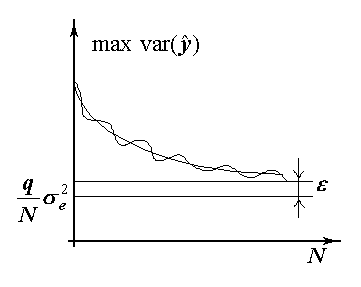
Выбор стратегии планирования, то есть числа планируемых опытов на каждом этапе, должен производиться из следующих соображений:

1) Если планируется один опыт на каждом этапе, то каждый такой опыт является наиболее информативным, так как он планируется после уточнения оценок неизвестных параметров модели. Однако при такой стратегии сильно затягивается реализация процедуры во времени, так как после каждого опыта требуется вычисление коэффициентов, увеличиваются и вычислительные затраты.

2) Если планируется сразу несколько опытов, то информативность каждого такого опыта снижается, так как они планируются без уточнения коэффициентов, но при этом резко сокращаются вычислительные затраты, и ускоряется процедура идентификации.

ПОСТРОЕНИЕ ОПТИМАЛЬНЫХ МОДЕЛЕЙ ТИПА "ВХОД - ВЫХОД".

Задача оптимального восстановления
ординат импульсной переходной функции

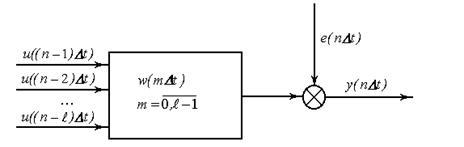
В задачах динамики в качестве факторов планирования выступают дискретные значения входного сигнала в моменты времени, предшествующие моменту планируемого измерения выхода, т.е.:

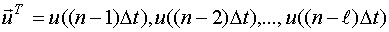
Задать значение вектора 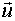- значит задать предысторию по входу.

Вектор факторов планирования однозначно определяет сигнал, длительностью 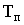, который является предысторией по входу, если планируемое измерение выхода производится в момент окончания этого участка сигнала (если входной сигнал является кусочно-постоянной функцией на интервале t).

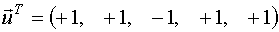
Пространство планирования U₀ обычно задается следующим образом:

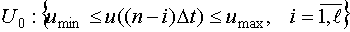
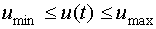- ограничение входного сигнала по амплитуде.

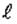- дискретное время памяти.

В задачах динамики также используются нормированные факторы, если соответствующая модель линейно параметризованная.

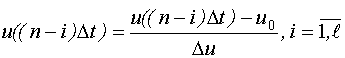
где 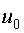- значение входного сигнала объекта до начала эксперимента.

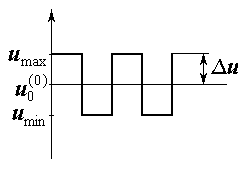
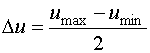- интервал варьирования.

.

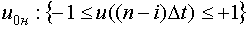План эксперимента в задачах динамики также определяется спектром и частотами. Последовательность точек плана определяет непрерывный тестирующий сигнал, который должен быть подан на вход объекта при реализации плана.

Рассмотрим пример для 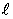=4.

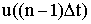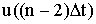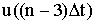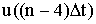+1	-1	+1	-1
+1	+1	-1	-1
-1	-1	-1	+1	сшивается на три такта
+1	+1	-1	+1
-1	+1	+1	+1	сшивается на два такта
+1	-1	+1	+1	сшивается на три такта

"Сшивание":

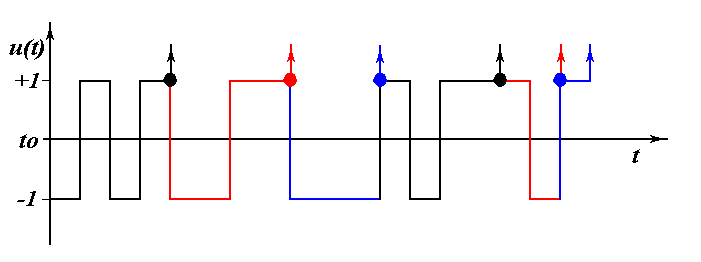
Построение сигнала на базе плана производится либо путем "стыковки" участков сигнала, определенных соседними точками плана, либо путем их "сшивания" на максимально возможную глубину. "Сшивание" возможно на 1,2,..., 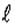-1 такт. При сшивании можно существенно сократить длину сигнала и протяженность эксперимента.

При построении непрерывного сигнала на базе плана имеются следующие возможности уменьшения длины сигнала:

1) Определение такой последовательности реализаций точек плана, которая обеспечивает минимальную длину сигнала. Нужно выбрать такую последовательность, при которой наибольшая "сшиваемость".

2) Учет свойств эквивалентности симметричных участков сигнала.

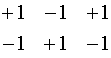- эти участки сигнала несут одинаковую информацию.

Дисперсия в симметричных точках одинакова, то есть можно менять знаки на противоположные.

Если это свойство выполняется, то при построении сигнала ординаты отдельных участков можно заменить на симметричные им значения и обеспечить тем самым большую глубину их сшивания.

Критерии оптимальности в задачах динамики те же, что и в задачах статики. Но эти критерии относятся обычно не к планам, а к определяемым ими тестирующим сигналам.

В задачах планирования эксперимента при синтезе моделей динамики реализуются два этапа:

1) синтез оптимального плана для заданной структуры динамической регрессионной модели и выбранного критерия оптимальности;

2) построение непрерывного тестирующего сигнала минимально возможно длины на основе синтезированного плана.

При планировании эксперимента в динамике моменты измерения выхода априори неизвестны. Они определяются лишь после построения тестирующего сигнала. Как правило, эти моменты неравноотстоящие. Минимальный интервал равен t, а максимальный интервал - .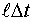

В общем случае, обработка результатов эксперимента методом наименьших квадратов возможна, когда время корреляции случайного процесса 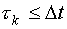.Таким образом, шаг дискретизации можно выбрать первоначально из того же условия. Но это только один аспект выбора шага дискретизации.

Особенности выбора шага дискретизации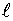

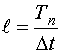
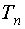всегда определено.

 tи 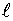нужно определить.

Параметр 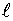можно рассматривать как дополнительный фактор планирования, то есть при синтезе оптимального тестирующего сигнала параметр 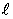можно варьировать и находить некоторое оптимальное его значение.

При выборе 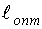можно исходить из следующих соображений:

1) целью задачи синтеза оптимального тестирующего сигнала является определение оптимальной формы сигнала как функции времени, то есть точное определение моментов переключения сигнала;

2) если 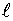или tвыбраны неудачно, то оптимальный сигнал может не быть синтезирован только потому, что точные моменты переключения отличаются друг от друга на величины,не кратныеt.

Два участка сигнала,полученные при кратных значениях 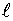совпадают по форме.

1. 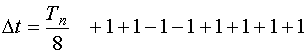2. 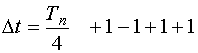, то форма сигнала не изменится.

Учитывая то, что два участка сигнала, полученные при кратных значениях 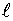совпадают по форме, если t выбрано оптимально, можно предложить следующий алгоритм оптимизации :

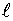1) Задается .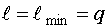

2) Синтезируется участок сигнала, соответствующий 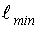. Для этого участка вычисляется критериальная функция .

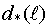3) 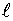увеличивается в два раза: .

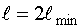4) Синтезируется участок сигнала для 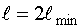. Вычисляем для этого участка критериальную функцию .

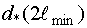5) Сравниваются по модулю: 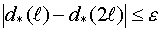. Если это условие выполняется, задача решена. Если не выполняется, то задается новое значение 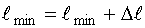, при чем 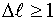и реализуются этапы 2-5.

После определения 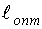в качестве искомого тестирующего сигнала необходимо использовать удовлетворяющий условию останова сигнал, а моменты измерений выхода определяются как моменты окончания участков тестирующего сигнала (максимально возможно сшитого).

Оптимизация параметра 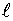обычно производится один раз при синтезе первого участка тестирующего сигнала, то есть первой точки плана. При определении остальных участков сигнала (точек плана) используется 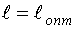или минимально возможное кратное ему значение.

Оптимальное восстановление ординат
импульсной переходной функции

Ранее была получена структура модели ординат:

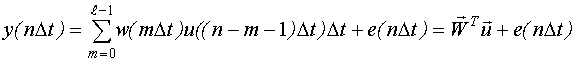
с вектолром неизвестных параметров

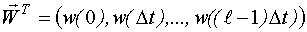
Необходимо найти оптимальные оценки неизвестных ординат.

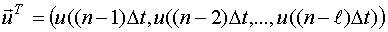- вектор входных переменных или факторов планирования.

По структуре данная модель эквивалентна модели: 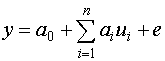, если обозначить .

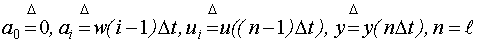Таким образом, задача оптимального восстановления ординат и.п.ф. может быть решена на основе ортогональных планов первого порядка типа ПФЭ и ДФЭ. Это следует из эквивалентности моделей.

Рассмотрим пример.

Пусть 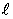=3. ПФЭ для такой модели является одновременно ортогональным, рототабельным, D- и G-оптимальным планом.

План будет иметь вид:

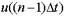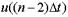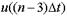+1	+1	+1
-1	+1	+1
+1	-1	+1
-1	-1	+1
+1	+1	-1
-1	+1	-1
+1	-1	-1
-1	-1	-1

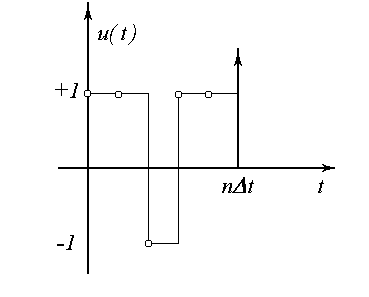
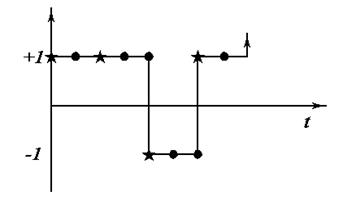
Этому плану будет соответствовать следующий тестирующий сигнал:

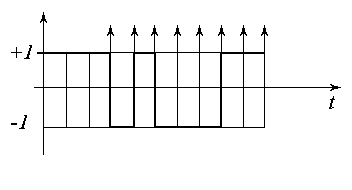
Стрелками указаны моменты планируемых измерений выхода.

Таким образом, оптимальные тестирующие сигналы для восстановления ординат могут быть построены на основе ортогональных планов первого и второго порядка типа ПФЭ и ДФЭ. Однако обеспечить минимальную длину сигнала на основе таких планов не всегда возможно.

ПЛАНЫ ПЛАККЕТТА-БЕРМАНА.

Большими возможностями для построения оптимальных тестирующих сигналов обладают ортогональные планы Плаккетта-Бермана.

Эти планы могут быть построены на основе соответствующих последовательностей символов +1 и -1. Такие последовательности получены для различных значений N (N - общее число точек плана) от 8 до 100 с шагом 4, кроме N=92. Каждая последовательность содержит N-1 символ и определяет ортогональный план Плаккетта-Бермана, матрица которого имеет размерность .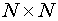

Рассмотрим последовательность для N=16.

+1 +1 +1 +1 -1 +1 -1 +1 +1 -1 -1 +1 -1 -1 -1

На основе этой последовательности можно построить матрицу плана следующим образом: последовательность символов принимается в качестве первых N-1 элементов первого столбца матрицы.

Второй столбец получается на основе первого столбца следующим образом: в качестве первого элемента второго столбца используется последний элемент первого столбца, то есть элементы первого столбца сдвигаются на один элемент вниз и переписываются во второй столбец. Остальные столбцы заполняются аналогично. Шестнадцатая строка заполняется ⌠√1■.

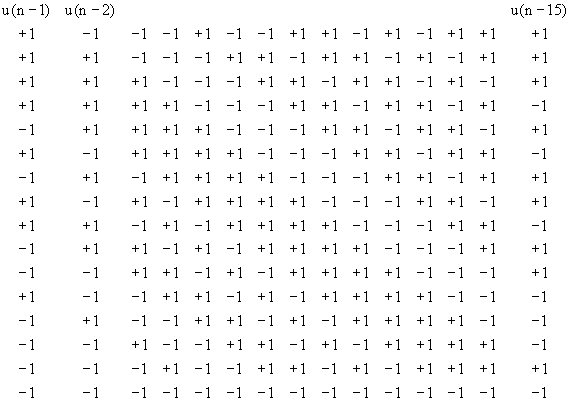
Построенному плану Плаккетта-Бермана будет соответствовать следующий тестирующий сигнал:

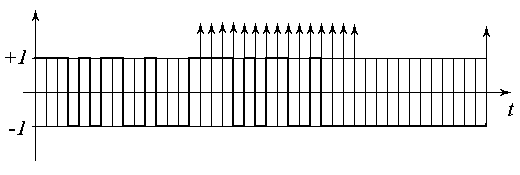
Это оптимальный сигнал для восстановления 15 ординат и.п.ф.

Матрица плана Плаккетта-Бермана является ортогональной и удовлетворяет всем трем свойствам матриц ортогональных планов первого порядка.

Сигналы, построенные на основе ПФЭ, ДФЭ и планов Плаккетта-Бермана, близки к псевдослучайным двоичным сигналам (ПСДС). Сигнал, построенный на основе плана Плаккетта-Бермана, может быть использован для нахождения оптимальных оценок до N-1 ординаты и.п.ф.

Для повторения сигнала можно использовать его симметричное отражение, чтобы увеличить глубину "сшивания".

Если измерения выхода не сопряжены с экономическими затратами, то после реализации тестирующего сигнала на объекте при вычислении оценок можно использовать не только запланированные измерения выхода, но и все дополнительные измерения (промежуточные), определивдля них соответствующую предысторию по входу. При этом оценки неизвестных параметров могут ухудшаться, однако точность оценок повышается.

Если используется МНК необходимо, чтобы выполнялось условие: 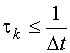. При невыполнении этого условия следует использовать ОМНК.

Если 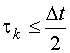, то можно повысить точность модели без повторного тестирования объекта, если при обработке информации использовать и промежуточные измерения выхода. Промежуточные измерения выхода возможны, так как входной сигнал является кусочно-постоянной функцией времени и, следовательно, предыстория для каждого промежуточного измерения выхода та же, что и для измерения, производимого в начальный момент соответствующего интервала времени, то есть для планируемого измерения.

Построение D-оптимальных моделей,
соответствующих разложению импульсной переходной функции по системе базисных функций

Структура такой модели была получена в виде:

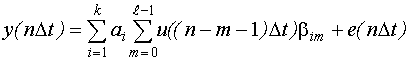
Эта модель соответствует разложению импульсной переходной функции по системе базисных функций:

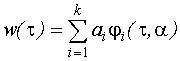
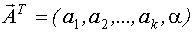- вектор неизвестных параметров.

Анализируя структуру линейно-комбинационной модели, легко видеть, что для нее неизвестны оптимальные планы. Для данной модели синтезировать ортогональный или рототабельный план невозможно, поэтому будем использовать критерий D-оптимальности.

Будем рассматривать два подхода к построению D-оптимальной линейно-комбинационной модели:

1. Построение D-оптимальной линейно-параметризованной модели.

2. Построение нелинейно-параметризованной D-оптимальной модели.

При первом подходе будем решать задачу априорного планирования эксперимента и задачу априорного синтеза D-оптимального тестирующего сигнала. При втором подходе будем использовать теорию последовательного планирования эксперимента и синтезировать локальный D-оптимальный тестирующий сигнал в реальном масштабе времени.

ПОСТРОЕНИЕ D-ОПТИМАЛЬНОЙ ЛИНЕЙНО-ПАРАМЕТРИЗОВАННОЙ,
ЛИНЕЙНО-КОМБИНАЦИОННОЙ ДИНАМИЧЕСКОЙ РЕГРЕССИОННОЙ МОДЕЛИ

Априорная оценка параметра затухания системы базисных функций равна:

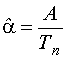
Вектор неизвестных параметров модели:

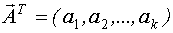
Мы должны построить модель, для которой .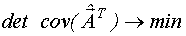

Для этого необходимо найти D-оптимальный план для линейно-комбинационной модели при известном  и построить тестирующий сигнал на основе этого плана, то есть построить непрерывный D-оптимальный тестирующий сигнал.

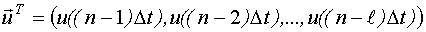- факторы планирования.

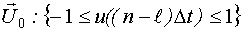
Синтез непрерывного D-оптимального плана будем производить на основе ПНП:

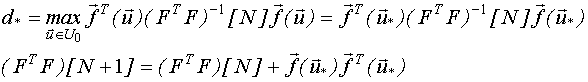
В качестве начального плана можно использовать любой ортогональный план (ПФЭ и ДФЭ и другие), а в качестве начального участка тестирующего сигнала использовать соответствующий сигнал, предназначенный для восстановления ординат.

Этот план предполагает 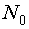измерений выхода. Вычисление информационной матрицы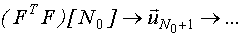

Рассмотрим особенности реализации ПНП для линейно-комбинационной модели.

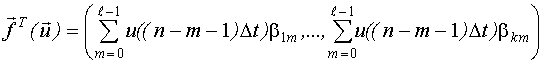
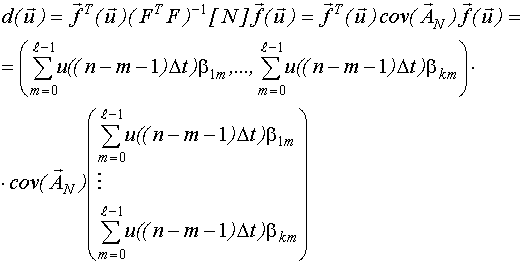
Важное значение имеет исследование дисперсионной функции 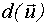и определение множества точек пространства планирования, в котором она может достигать глобального максимума. После нахождения такого множества поиск глобального максимума можно производить путем вычисления дисперсионной функции в точках этого множества и выбирать ту точку, где дисперсия максимальна.

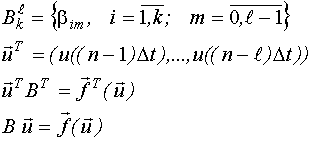
Наша дисперсионная функция .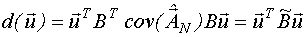

Таким образом, мы показали, что дисперсионная функция является квадратичной формой относительно вектора 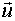. Отсюда следует, что максимумы этой функции могут достигаться лишь на границах области планирования. Отсюда следует, что синтезируемый D-оптимальный тестирующий сигнал является двухуровневым, то есть может принимать значения ╠ 1. Таким образом, мы показали, что только в вершинах пространства планирования дисперсионная функция может достигать глобальных максимумов, число которых равно 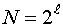. Очевидно, что в симметричных точках пространства планирования дисперсия предсказания выхода одинакова.

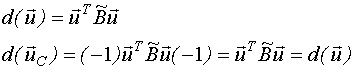
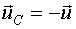- симметричная точка.

Таким образом, мы показали, что симметричные участки тестирующего сигнала эквивалентны. Это свойство необходимо использовать при сливании строк матрицы планирования с целью уменьшения длины соответствующего сигнала. Это свойство позволяет в два раза сократить число просматриваемых точек пространства планирования, то есть число просматриваемых точек будет .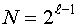

Известна теорема, согласно которой необходимо просматривать лишь те вершины пространства планирования, которым соответствуют участки сигнала, имеющие не более (k-1) переключения.

Предположим, что к=3.

0 переключений

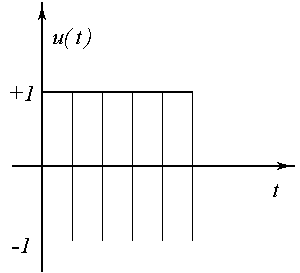
участки с 1-им переключением

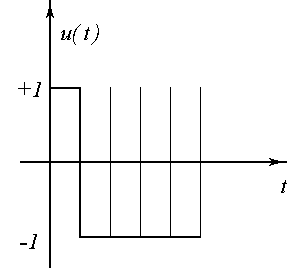
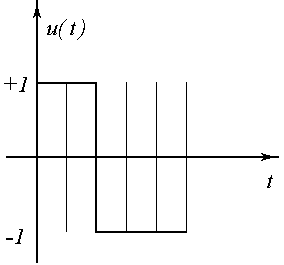
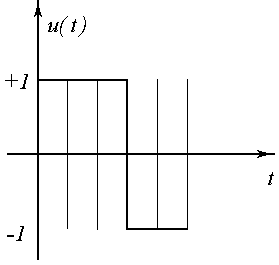
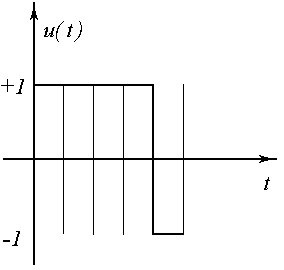
участки с 2-мя переключениями

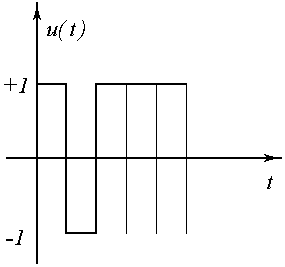
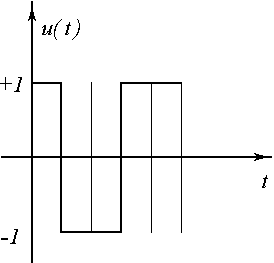
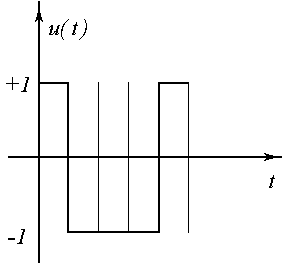
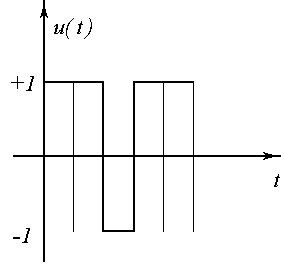
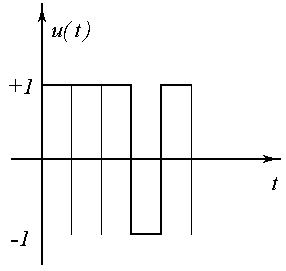
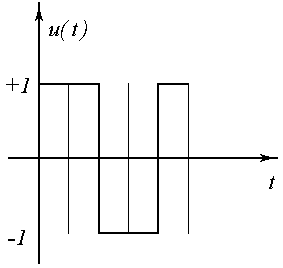
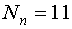- число вариантов

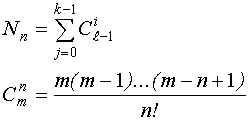
Реализация ПНП в данной задаче производится также как и в задаче статики с учетом результатов данной теоремы.

На первой итерации определяется оптимальная глубина памяти ( 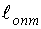). В результате находится план и строится тестирующий сигнал, построение которого производится также, как и восстановление ординат с учетом эквивалентности симметричных участков сигнала.