Вычисление МНК-оценок неизвестных параметров. Определение дисперсий оценок

РЦКП

ИДЕЯ МЕТОДА БОКСА-УИЛСОНА

Задача статической оптимизации сводится к определению таких значений входных параметров, при которых выход объекта принимает экстремальное значение.

Метод Бокса-Уилсона представляет собой совокупность метода крутого восхождения и методов планирования экспериментов. Он основан на понятии градиента.

Градиент - это вектор, направленный в сторону максимально быстрого возрастания функции

,

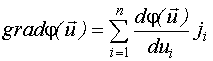где 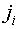- единичная орта, направленная вдоль i-ой оси

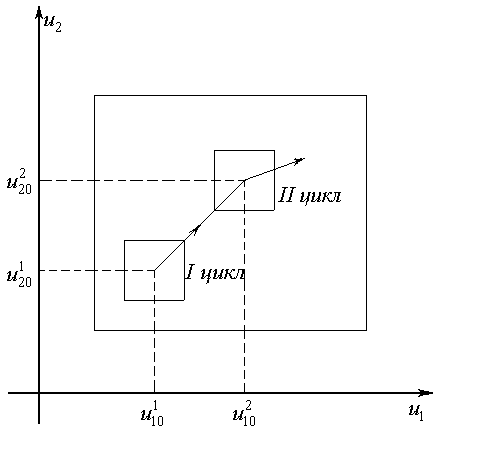
Метод Бокса-Уилсона ортогональные планы первого порядка реализует на каждом цикле крутого восхождения, при этом исходная точка каждого цикла принимается центром области планирования. Задается область планирования, по результатам реализации плана оценивается направление градиента и осуществляется движение вдоль этого направления. Процесс оптимизации заканчивается на том цикле, в начале которого все компоненты вектора градиента статистически незначимы.

Задаем начальную точку 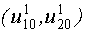и область планирования 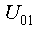. Проводим полный факторный эксперимент. Находим .

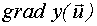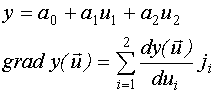
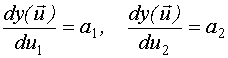
Первый цикл крутого восхождения начинается с точки, соответствующей центру исходной области планирования. Из этой точки начинается движение в сторону градиента, при этом чередуются мысленные и реализуемые опыты.

Мысленный опыт - опыт, не реализуемый на объекте и заключающийся лишь в переходе от одной точки, расположенной в направлении градиента, к другой. Опыт сводится к пересчету координат. Для пересчета необходимо знать шаг движения по градиенту.

Реализуемый опыт √ это опыт, который производится в соответствующей точке, расположенной на направлении градиента.

Первый цикл крутого восхождения заканчивается на том реализуемом опыте, которому соответствует максимальное значение выхода. Эта точка принимается в качестве центра области планирования для оценки направления градиента для второго цикла.

После оценки параметров модели на каждом цикле необходимо проверить их статистическую значимость с тем, чтобы определить является ли предыдущий планируемый цикл завершением процедуры оптимизации.

ПРИМЕР РЕАЛИЗАЦИИ МЕТОДА БОКСА-УИЛСОНА.

Факторы	Хром Cr	Никель Ni	Молибден Mo	Ванадий V	Ниобий Nb	Марганец Mn	Углерод C
Основ.уровни,% Интервал варьирования,% Верхний +1 Нижний √1			0,1 0,1 0,2	0,02 0,02 0,04	0,1 0,1 0,2	0,4 0,1 0,5 0,3	0,4 0,1 0,5 0,3	Сопротивление на разрыв при t=800╟С
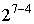- реплики	-1 +1 +1 -1 +1 -1 -1 +1	-1 +1 -1 +1 -1 +1 -1 +1	-1 -1 +1 +1 -1 -1 +1 +1	-1 -1 -1 -1 +1 +1 +1 +1	-1 +1 +1 -1 -1 +1 +1 -1	-1 +1 -1 +1 +1 -1 +1 -1	-1 -1 +1 +1 +1 +1 -1 -1	4,5 3,5 6,2 3,2 5,3 5,1 5,3 5,8
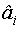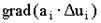(МНК) Шаг движения по Округл. шаг	0,71 0,71 0,8	-0,09 -0,09 -0,1	0,65 0,064 0,07	0,89 0,018 0,02	0,54 0,054 0,06	0,16 -0,016 -0,02	0,46 0,04 0,05
Мысленные 1 опыты 2	4,8 7,2	1,9 1,6	0,17 0,38	0,04 0,1	0,16 0,34	-0,38 -0,32	0,45 0,6
Реализованный опыт 9 Мысленный опыт 5 Реализованный опыт 10	8,0 8,8 9,6 10,4 11,2 12,0	1,5 1,4 1,3 1,2 1,1 1,0	0,45 0,52 0,59 0,66 0,73 0,80	0,12 0,44 0,16 0,18 0,2 0,22	0,4 0,46 0,52 0,58 0,64 0,70	0,3 0,28 0,26 0,24 0,22 0,2	0,65 0,7 0,75 0,80 0,85 0,9	10,3 11,0 11,5 11,2 10,1

Округления производятся таким образом, чтобы соответствующие исходным и округленным значениям вектора мало отличались друг от друга по направлению.

НАЗНАЧЕНИЕ И ТИПЫ ПЛАНОВ ВТОРОГО ПОРЯДКА.

Назначение этих планов - построение квадратичных регрессионных статических моделей.

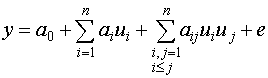
Пусть n=2

Тогда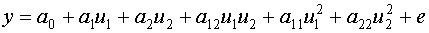

Это квадратичная модель, она может быть более адекватна, чем линейная модель.

Планы факторного эксперимента первого порядка неприменимы, так как:

1) они являются двухуровневыми, а через две точки нельзя провести кривую второго порядка;

2) они не позволяют раздельно оценить свободный член модели и коэффициенты при квадратичных переменных.

Существуют специальные планы, которые позволяют строить квадратичные модели регрессии - планы второго порядка.

Существуют три типа таких планов:

1) полный факторный эксперимент (ПФЭ) типа ;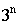

2) ортогональные центральные композиционные планы (ОЦКП);

3) рототабельные центральные композиционные планы (РЦКП).

Полный факторный эксперимент типа .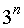

Это трехуровневый план, спектр которого включает в себя вершины пространства планирования, середины ребер n-мерного гиперкуба и центр пространства планирования. Частоты повторения в всех точках спектра одинаковы.

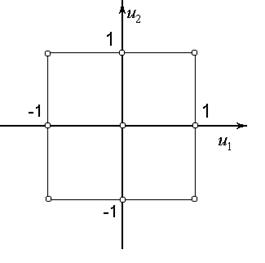
u1	u2
+1	+1
	+1
-1	+1
+1
-1
+1	-1
	-1
-1	-1

Основной недостаток такого планирования - чрезмерная избыточность, то есть большое число экспериментов.

Композиционные планы (ОЦКП, РЦКП)

Композиционные планы имеют одинаковую структуру и состоят из трех блоков:

1 блок √ ортогональный план первого порядка (ПФЭ или чаще ДФЭ).

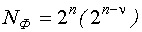- число точек первого блока.

2 блок - звездные точки, то есть точки, расположенные на координатных осях и удаленные от центра области планирования на величину звездного плеча .

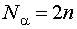- число звездных точек.

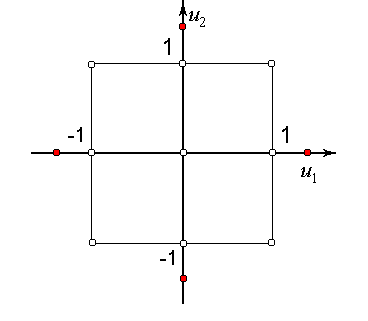
3 блок - центральные точки (точки, расположенные в центре области планирования (ОП)).

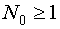- число центральных точек.

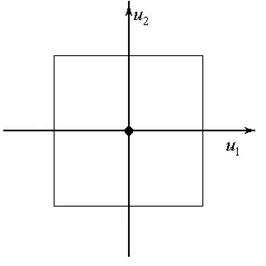
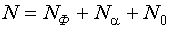- общее число точек плана.

В общем случае такие планы являются пятиуровневыми, так как факторы варьируются на пяти уровнях: - , -1, 0, +1,  .

Поэтому при исследовании реального объекта с неизвестной структурой модели область планирования не должна включать всю область экспериментирования (ОЭ), так как при получении неадекватной линейной модели уточнить структуру в классе квадратичных не удастся из-за невозможности реализации звездных точек.

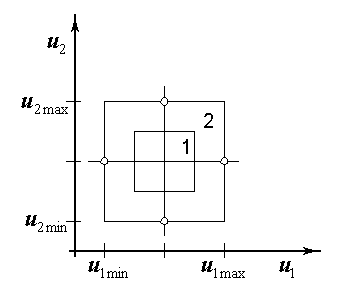
1 √ ОП

2 √ ОЭ

Необходимо так выбирать интервал варьирования, чтобы выполнялось соотношение: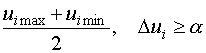

Отличие ОЦКП и РЦКП заключается в значениях параметров  и 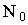. Для ОЦКП 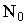=1, для РЦКП 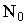>1.

ОЦКП

Ортогональные центральные композиционные планы (ОЦКП) предназначены для построения квадратичной модели.

Приведем пример ОЦКП.

n		N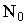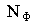			N	3n
	1,0
	1,215
	1,414

n √ число факторов.

1 блок √ ПФЭ.

Чем больше число факторов, тем эффективнее ОЦКП по сравнению с ПФЭ типа 3ⁿ.

При n=2 ОЦКП совпадает с ПФЭ типа 3ⁿ.

Структура ОЦКП

n=3

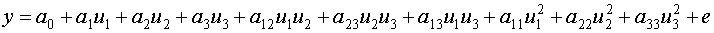
		z0	z1	z2	z3	z4	z5	z6				z7	z8	z9
	u0	u1	u2	u3	u1u2	u1u3	u2u3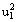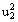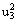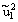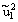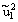
		+1	+1	+1	+1	+1	+1		0.27	0.27	0.27
		-1	+1	+1	-1	-1	+1	0.27	0.27	0.27
		+1	-1	+1	-1	+1	-1	0.27	0.27	0.27	Первый
		-1	-1	+1	+1	-1	-1	0.27	0.27	0.27	блок
		+1	+1	-1	+1	-1	-1	0.27	0.27	0.27	ПФЭ
		-1	+1	-1	-1	+1	-1	0.27	0.27	0.27
F=		+1	-1	-1	-1	-1	+1	0.27	0.27	0.27
		-1	-1	-1	+1	+1	+1	0.27	0.27	0.27
		1.215				1.2152			0.75	-0.73	-0.73
		-1.215			1.2152			0.75	-0.73	-0.73	Второй
			1.215			1.2152		-0.73	0.75	-0.73	блок
			-1.215			1.2152		-0.73	0.75	-0.73	ПФЭ
				1.215			1.2152	-0.73	-0.73	0.75
				-1.215			1.2152	-0.73	-0.73	0.75
											-0.73	-0.73	-0.73	центральная
													точка
			ОЦКП для трех факторов

Анализируя полученную матрицу, состоящую из первых десяти столбцов, легко увидеть, что для нее не выполняются все три свойства матриц базисных функций ортогональных планов первого порядка.

Третье свойство выполняется только для первых семи столбцов, т.е. эти столбцы попарно ортогональны.

Второе свойство выполняется лишь в пределах каждой группы столбцов (1-ая группа ╝1 столбец ( 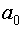); 2-ая группа ╝2-4 столбцы ( 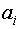); 3-я группа ╝ 5-7 столбцы ( 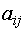); 4-ая группа ╝ 8-10 столбцы ( ).

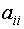Запишем информационную матрицу:

		8+1.2152

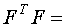Недиагональная часть матрицы появляется за счет того, что последние три столбца неортогональны с другими столбцами и между собой.

Таким образом, полученная матрица не является диагональной, и на ее основе невозможно получить некоррелированные оценки всех неизвестных коэффициентов.

Для обеспечения ортогональности соответствующей ОЦКП матрицы базисных функций необходимо произвести замену квадратичных переменных.

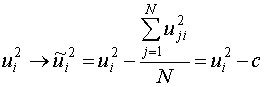
Для нашего плана с=0,73 √ это константа плана.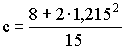

Полученная таким образом матрица F является полностью ортогональной.
Таким образом, матрица (F^TF), соответствующая преобразованной матрице F, является диагональной. Причем,диагональные элементы одинаковы лишь в пределах каждой группы элементов.
Диагональные элементы информационной матрицы уменьшаются при переходе от одной группы коэффициентов к другой. Соответствующие элементы ковариационной матрицы оценок увеличиваются при переходе от одной группы к другой.
Таким образом, при реализации ОЦКП оценки неизвестных коэффициентов модели имеют разную дисперсию, то есть находятся с неодинаковой точностью. Точнее всего оценивается свободный член, с меньшей точностью - коэффициенты при линейных членах ( 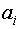), еще с меньшей точностью √ коэффициенты при парном взаимодействии ( 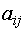). Самые неточные оценки - у коэффициентов при квадратичных членах ( 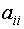). В пределах одной группы эти оценки не изменяются.
Вычисление МНК-оценок неизвестных параметров.

Определение дисперсий оценок

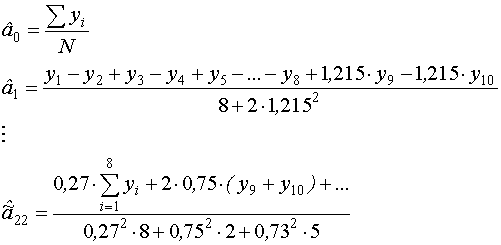
Оценка i-ого коэффициента определяется следующим образом:

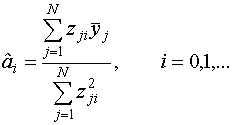
После вычисления МНК оценок необходимо в регрессионную модель подставить выражение для преобразованных квадратов.

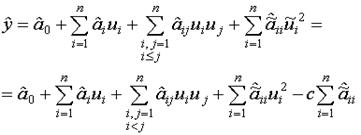
Окончательная модель имеет вид:

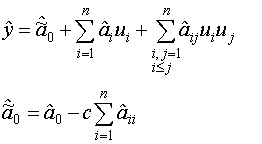
Дисперсии оценок неизвестных коэффициентов полученной модели определяются следующим образом:

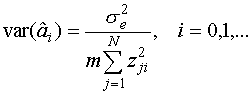
Для этой оценки число степеней свободы =N(m-1), где m-число повторений ОЦКП.

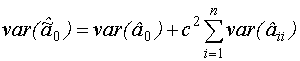
РЦКП

Особенность рототабельных центральных композиционных планов (РЦКП) состоит в том, что:
1) число центральных точек N_{0 >1;}
2) величина звездного плеча ;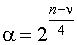
3) вычисление оценок неизвестных параметров производится по более сложным формулам, чем в ОЦКП.

Приведем пример РЦКП

n		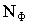	N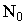		N
		1,414
		1,682

Были проведены исследования выражения 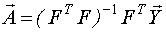, и получены аналитические выражения для МНК-оценок всех групп коэффициентовмодели. Аналитические выражения для оценок неизвестных параметров модели и дисперсий оценок базируются на трех константах, которые вычисляются на основе матрицы РЦКП.

Первая константа 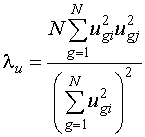, берутся любые i-й и j-й столбцы

Вторая константа 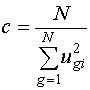, берется любой i-й столбец

Третья константа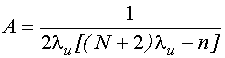

Эти константы получаются на основе использования любых двух квадратичных столбцов.

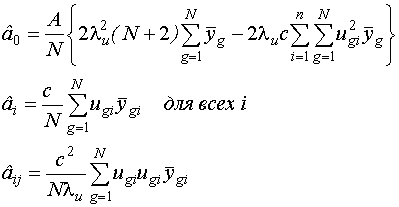
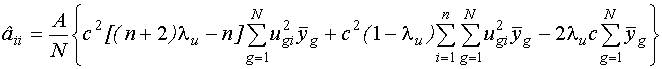
Выражения для дисперсийоценок:

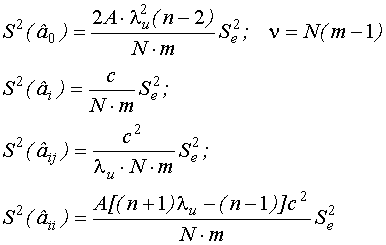
Тема 14. D - оптимальное планирование

14.1. D - оптимальные планы

14.2. Процедура непрерывного планирования (ПНП)

D - ОПТИМАЛЬНЫЕ ПЛАНЫ

Поскольку D и G-критерии эквивалентны, при синтезе D-оптимальных планов целесообразнее опираться на критерий G-оптимальности, то есть условие: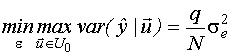

Построение непрерывных D-оптимальных планов осуществляется с помощью процедуры непрерывного планирования (ПНП) Вучкова-Соколова-Федорова.

Синтез точных планов предполагает решение многомерной задачи комбинаторного анализа, что не всегда возможно на практике. Поэтому проще решать задачу планирования D-оптимального эксперимента в следующей последовательности:

1) синтезировать D-оптимальный план с помощью процедуры непрерывного планирования (ПНП);
2) задать приемлемое число экспериментов;
3) округлить непрерывный план.

Процедура непрерывного планирования (ПНП)

Это поэтапная процедура, на каждом этапе которой решается задача синтеза одной точки искомого непрерывного D-оптимального плана, для чего решается задача, задаваемая следующими матричными выражениями:

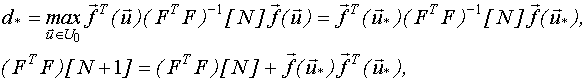
где N - номер этапа процедуры;

d - дисперсия предсказания выхода.

Процедура реализуется с помощью двух матричных выражений:

первое выражение реализует задачу нахождения точки 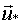, принадлежащей пространству планирования ( 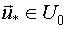), где дисперсия предсказания выхода максимальна;

второе выражение реализует включение точки 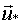в план эксперимента; то есть коррекции информационной матрицы Фишера.

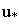- точка, где модель работает хуже всего; поэтому здесь нужно провести еще один эксперимент.

Покажем, что информационная матрица Фишера для N+1 опыта равна сумме информационных матриц для каждого опыта.

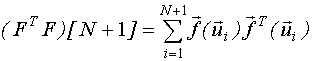
Пусть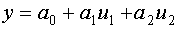

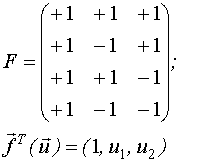
Информационная матрица для четырех опытов.

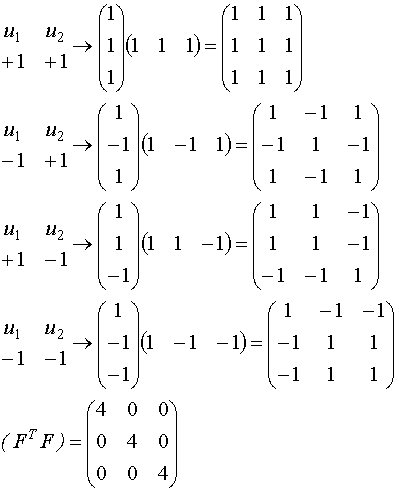
Покажем это в общем виде.

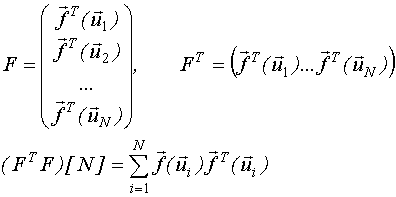
Обычно ПНП реализуется в следующей последовательности:

Задается произвольный невырожденный план, то есть план, на основе которого можно оценить все неизвестные коэффициенты модели, для которой синтезируется D-оптимальный план.

План называется невырожденным, если определитель соответствующей ему информационной матрицы не равен нулю. При этом необходимо, чтобы число опытов было больше числа коэффициентов, то есть .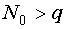

Обычно в качестве начального плана используются известные для данной модели планы (ПФЭ, ДФЭ). Если же известные планы не подходят, то можно использовать произвольный план из 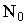точек. Сначала нужно убедиться, что он невырожденный.

Данная процедура используется дважды при синтезе D-оптимального плана:

1) для определения спектра плана;

2) для определения частот повторения наблюдения.

На этапе определения спектра поиск глобального максимума квадратичной формы производится по всем точкам пространства планирования. При этом используется один из методов статической оптимизации (например, симплекс-метод). Поэтому при синтезе D-оптимальных планов необходимо исследовать соответствующую квадратичную форму и постараться упростить задачу поиска глобального максимума. Результатом такого решения должно быть сокращение пространства поиска глобального максимума.

ПНП реализуется в следующей последовательности:

1) задается начальный план ( 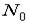точек);

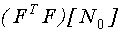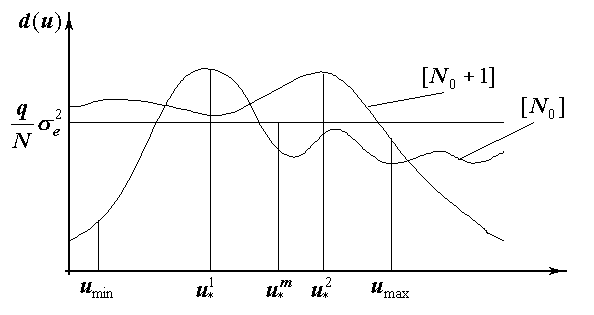
2) для него вычисляется информационная матрица , полученная матрица подставляется в первое уравнение, решается задача оптимизации и находится точка 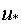. Задача оптимизации решается методом сеток

3) точка 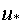включается в план, становится 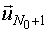и происходит корректировка информационной матрицы;

4) полученное значение информационной матрицы 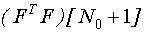подставляется в первое уравнение;

5) находится новая точка 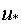, которая вновь включается в план, корректируется информационная матрица и т. д.

Процедура реализуется до тех пор, пока максимальное значение дисперсии предсказания выхода не станет близким к .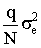

Однако на этапе определения спектра нет необходимости повторять этапы ПНП до выполнения правила останова вида: 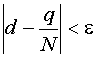, т.к. для этого требуется много машинного времени для решения задачи на каждом этапе.

В ПНП используется ковариационная матрица с 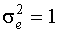, так как при решении задачи оптимизации умножение функции на константу не изменяет координаты ее экстремума.

Известно, что для выявления спектра непрерывного D-оптимального плана этапы ПНП достаточно повторить 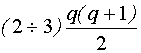раз, так как спектр плана включает не более, чем 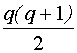точек, где q-число коэффициентов модели.

На этапе определения частот также используется ПНП, но во-первых, в качестве начального плана используется план, включающий по одному разу все точки спектра; во-вторых, поиск максимума квадратичной формы производится лишь в точках спектра плана (в других точках максимума быть не может); в качестве начального плана берется такой план, который не включает "лишних" точек, в которых наверняка нет максимума; в-третьих, ПНП реализуется до выполнения правила останова.

В качестве D-оптимального плана принимается план, включающий начальный план этапа определения частот, то есть все точки спектра и все точки 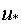, определенные на итерациях процедуры вплоть до выполнения правила останова.

После определения последовательности точек непрерывного D-оптимального плана необходимо рассчитать частоты повторения наблюдений в точках спектра. Совокупность частот и спектра и определяет искомый D-оптимальный план. При реализации плана на объекте можно придерживаться той последовательности точек, которая была получена на этапе определения частот.

Если полученная последовательность точек плана при приемлемом числе экспериментов близка к D-оптимальной, то реализация плана на объекте может быть осуществлена путем ее предварительной рандомизации.

Если же при заданном числе опытов полученная последовательность точек сильно отличается от D-оптимальной последовательности, то необходимо воспользоваться непрерывным D-оптимальным планом с заданным спектром и частотами, округлить его до N, определить число повторений в каждой точке спектра и рандомизировать полученную таким образом последовательность опытов.

Тема 15. Последовательное планирование эксперимента.

Планирование эксперимента в динамике

Планирование эксперимента при нелинейной параметризации модели регрессии

15.2. Построение оптимальных моделей типа "вход-выход"

15.3. Особенности выбора шага дискретизации l