Векторные случайные величины И ИХ ХАРАКТЕРИСТИКИ

Векторная случайная величина - это совокупность нескольких случайных величин.

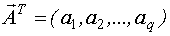
каждый элемент вектора 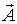характеризуется функцией распределения, моментными характеристиками и так далее.

Совокупность всех элементов вектора, называемая векторной случайной величиной, характеризуется:

1. многомерной функцией распределения;

2. ковариационной матрицей.

Многомерная функция распределения 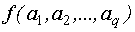имеет тот же смысл, что и для скалярных величин.

Рисунок

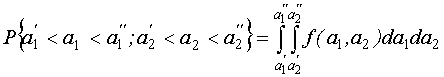
Если две случайные величины независимы, то совместная плотность распределения равна произведению плотностей распределения.

Ковариационная матрица обозначается 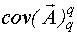и имеет следующую структуру:

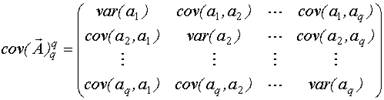
На главной диагонали ковариационной матрицы расположены дисперсии всех элементов случайного вектора. Элемент, стоящий на пересечении i-ой строки и j-го столбца равен ковариации i-го и j- го элементов вектора.

Ковариация двух случайных величин - это центральный смешанный момент 2-го порядка. Пусть есть две случайные величины - x и y.

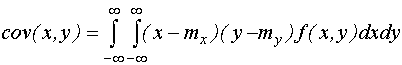
Ковариация - это коэффициент, определяющий степень линейной статистической зависимости двух случайных величин.

Зависимость двух случайных величин заключается в том, что распределение одной случайной величины зависит от значений другой случайной величины.

Ковариация связана с другим понятием, которое является мерой линейной статистической зависимости - коэффициентом корреляции.

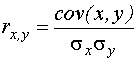
Коэффициент корреляции - это безразмерная величина, которая может принимать значения из отрезка [-1;+1].

Ковариация - это размерная величина, которая может принимать любые значения в зависимости от диапазона изменения величины.

Коэффициент корреляции - это нормированная ковариация.

Векторные случайные величины, являющиеся оценками неизвестных параметров моделей, так же характеризуется свойствами несмещенности, эффективности и состоятельности.

1. Несмещенный вектор оценок - это вектор с математическим ожиданием, равным истинному значению оцениваемого вектора.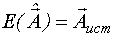
2.Состоятельность С ростом числа измерений N оценка приближается к истинной величине.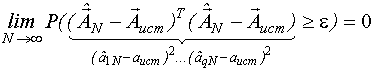

Пусть 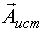- неизвестный вектор; 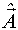- вектор оценок.

Качество оценивания неизвестных параметров математической модели характеризуется значениями элементов ковариационной матрицы, при этом необходимо стремиться к тому, чтобы дисперсии оценок были минимальными и ковариации каждой пары оценок стремились к нулю.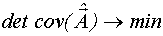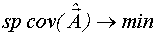

3. Оценка вектора 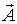эффективна, если ее ковариационная матрица в каком-то смысле минимально возможна.
След матрицы (sp) - это сумма диагональных элементов.

Тема 3. Методы оценивания неизвестных параметров

Регрессионных моделей

Метод наименьших квадратов

Корреляционная функция случайного процесса и ее свойства