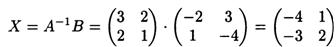Метод Гаусса решения систем линейных уравнений
Метод Гаусса называют также методом исключения переменных или двухходовым методом. Метод заключается в последовательном исключении переменных из уравнений системы (первой переменной из второго уравнения, первой и второй из третьего и т.д.) до тех пор, пока в последнем уравнении не окажется равенство вида pхn = q (p,q – числа), откуда естественным образом выражается последняя переменная хn. После этого, двигаясь по системе снизу вверх можно последовательно вычислить остальные неизвестные : хn-1 из предпоследнего уравнения, и т.д. до х1 из первого.
Рассмотрим квадратную систему
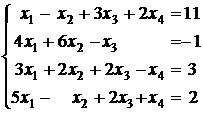 . (6)
. (6)
(Обратите внимание: во втором уравнении нет переменной х4 . Это значит, то а24=0. В последнем уравнении коэффициент при х2 , а42= -1, а при х4 , а44=1.
У этой системы коэффициент a11 отличен от нуля. Если бы это условие не выполнялось, то чтобы его получить, нужно было бы переставить местами уравнения, поставив первым то уравнение, у которого коэффициент при x1 не равен нулю.
Проведем следующие преобразования системы:
1) поскольку a11¹0, первое уравнение оставим без изменений;
2) вместо второго уравнения запишем уравнение, получающееся, если из второго уравнения вычесть первое, умноженное на 4;
3) вместо третьего уравнения запишем разность третьего и первого, умноженного на 3;
4) вместо четвертого уравнения запишем разность четвертого и первого, умноженного на 5.
Полученная новая система эквивалентна исходной и имеет во всех уравнениях, кроме первого, нулевые коэффициенты при x1 (это и являлось целью преобразований 1) – 4)):
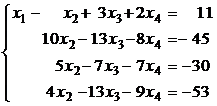 . (7)
. (7)
Можно доказать, что замена любого уравнения системы новым, получающимся прибавлением к данному уравнению любого другого уравнения системы, умноженного на любое число, является эквивалентным преобразованием системы.
Для проведения этого и дальнейших преобразований удобнее использовать расширенную матрицу системы. Тогда задачей первого этапа метода Гаусса будет приведение расширенной матрицы к трапециевидной форме – виду, когда в последней строке только два последних элемента ненулевые, в предпоследней строке – три и т.д. – см. матрицу и систему 9))
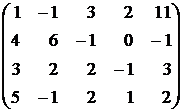 . (8)
. (8)
Преобразуем эту матрицу следующим образом:
1) первые две строки оставим без изменения, поскольку элемент a22 не равен нулю;
2) вместо третьей строки запишем разность между второй строкой и удвоенной третьей;
3) четвертую строку заменим разностью между удвоенной второй строкой и умноженной на 5 четвертой.
В результате получится матрица, соответствующая системе, у которой неизвестная x1 исключена из всех уравнений, кроме первого, а неизвестная x2 — из всех уравнений кроме первого и второго:
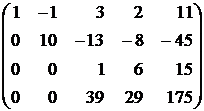 .
.
Теперь исключим неизвестную x3 из четвертого уравнения. Для этого последнюю матрицу преобразуем так:
1) первые три строки оставим без изменения, так как a33 ¹ 0;
2) четвертую строку заменим разностью между третьей, умноженной на 39, и четвертой:
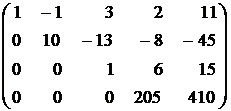 .
.
Полученная матрица соответствует системе
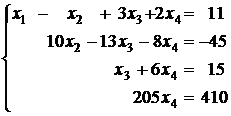 . (9)
. (9)
Из последнего уравнения этой системы получаем x4 = 2. Подставив это значение в третье уравнение, получим x3 = 3. Теперь из второго уравнения следует, что x2 = 1, а из первого — x1 = –1. Очевидно, что полученное решение единственно (так как единственным образом определяется значение x4, затем x3 и т. д.).
Назовем элементарными преобразованиями матрицы следующие преобразования:
1) перемена местами двух строк;
2) умножение строки на число, отличное от нуля;
3) замена строки матрицы суммой этой строки с любой другой строкой, умноженной на некоторое число.
Если матрица A является расширенной матрицей некоторой системы, и путем ряда элементарных преобразований матрицаAпереводится в матрицу B, являющуюся расширенной матрицей некоторой другой системы, то эти системы эквивалентны.
Назовем квадратную матрицу, у которой на главной диагонали стоят числа, отличные от нуля, а под главной диагональю – нули, треугольной матрицей. Матрица коэффициентов системы (9) – треугольная матрица.
Можно сформулировать общее правило:
Если с помощью элементарных преобразований матрицу коэффициентов квадратной системы можно привести к треугольной матрице, то система совместна и определенна
Метод обратных матриц
Рассмотрим уравнение в матричной форме АХ = В, Где А – матрица коэффициентов системы, Х – столбец неизвестных, В – столбец свободных членов.
Если бы речь шла об «обычном числовом» уравнении ax = b, a≠0, оно решалось бы умножением обеих частей уравнения на обратный к а элемент а-1 (1/a (делением на а))
1/a· ax = 1/a ·b и тогда x = b/a.
Тогда для уравнения АХ=В,
А-1 АХ = А-1 В, откуда решение находится по формуле Х = А-1 В, где А-1 - матрица, обратная к исходной матрице А
Это рассуждение применимо и к матричным уравнениям AX=B, где В является некоторой матрицей, необязательно вектор-столбцом. Х в таком случае будет просто некоторой матрице (см пример 5.2).
Определение 5.2(6).
Пусть A = (aij) – квадратная матрица с определителем, не равным нулю.
Тогда существует обратная матрица A–1, такая, что АA–1 = A–1А = Е (единичной матрице).
Найти обратную к А матрицу можно по формуле
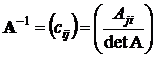 .
.
Последняя формула означает, что в i-й строке и j-м столбце обратной матрицы располагается алгебраическое дополнение элемента, стоящего в j-й строке и в i-м столбце исходной матрицы, деленное на определитель исходной матрицы.
Иначе говоря, обратная матрица находится делением на определитель исходной матрицы так называемой союзной матрицы – матрица, транспонированной к матриений (см. опр. 5.2(4)
.
Пример 5.2(1):
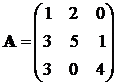 detA = 20 + 6 – 24 = 2;
detA = 20 + 6 – 24 = 2;
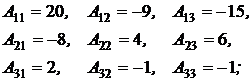
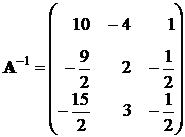 .
.
Из определения обратной матрицы следует, что она существует только для квадратной матрицы с определителем, отличным от нуля.
Свойства обратной матрицы
1. det A-1 = (det A)-1
Действительно, А A-1 = Е, следовательно, detA det A-1 = detE=1, откуда (det A)-1 =
=det A-1
2. Если А и В невырожденны, то их произведение АВ тоже невырожденно и
(АВ)-1 = В-1 А-1, то есть, матрица, обратная к произведению, равна произведению обратных, взятых в обратном порядке.
Действительно, (В-1 А-1)(АВ) = В-1 (А-1 А)В = В-1 В = Е.
Отсюда следует, что В-1 А-1 = (АВ)-1
3.(А-1 )-1 = А
Действительно, (А-1 )-1 есть такая единственная матрица, произведение которой на А-1 равно Е. Этим свойством обладает А
4. (АТ )-1 = (А-1 )Т .
Действительно, переходя в равенстве А А-1 = Е к транспонированным матрицам, получим (АТ )-1 АТ = Е, откуда следует, что (АТ )-1 = (АТ )-1
Пример 5.2(2)
Решить матричное уравнение АХ=В
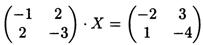
Будем искать решение в виде Х=А-1 В , т.к. А-1АХ = А-1 В
Найдем определитель матрицы А
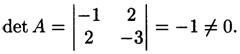
Определитель не равен нулю, значит, существуют единственное решение уравнения и матрица, обратная к матрице А. Найдем ее:
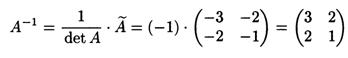
Теперь найдем решение уравнения